机器学习-->深度学习-->pytorch学习
本篇博文将大概的总结下深度学习框架pytorch的使用,其内容来自我在pytorch官方教程还有网上一些相关资料的总结,加上了一些自己的见解。
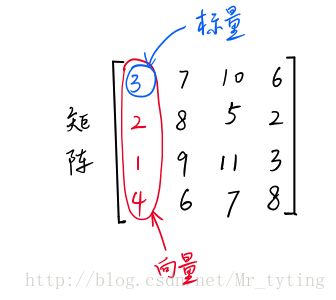
张量的说明
标量(Scalar)是只有大小,没有方向的量,如1,2,3等
向量(Vector)是有大小和方向的量,其实就是一串数字,如(1,2)
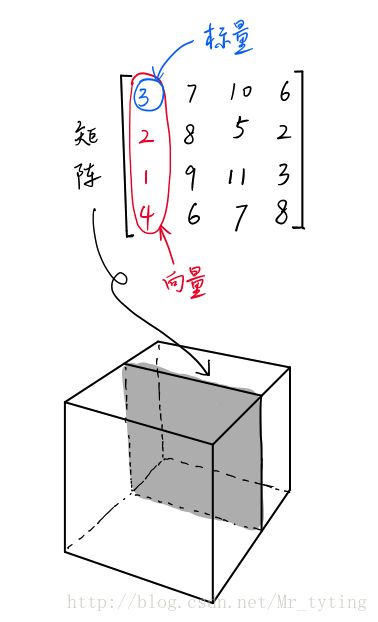
矩阵(Matrix)是好几个向量拍成一排合并而成的一堆数字,如[1,2;3,4]
标量,向量,矩阵它们三个也是张量,标量是零维的张量,向量是一维的张量,矩阵是二维的张量。
除此之外,张量还可以是四维的、五维等等。
代码示例:
import torch
x=torch.Tensor(2,3)##二维的张量
print x
1.0860e+32 4.5848e-41 7.0424e-38
0.0000e+00 4.4842e-44 0.0000e+00
[torch.FloatTensor of size 2x3]import torch
x=torch.Tensor(4,2,3)##三维张量
print x
(0 ,.,.) =
-7.7057e-06 4.5772e-41 -7.7057e-06
4.5772e-41 0.0000e+00 0.0000e+00
(1 ,.,.) =
0.0000e+00 0.0000e+00 0.0000e+00
0.0000e+00 8.1459e-38 0.0000e+00
(2 ,.,.) =
nan 0.0000e+00 7.7143e-28
2.5353e+30 1.8460e+31 1.7466e+19
(3 ,.,.) =
1.8430e-37 0.0000e+00 nan
nan 6.0185e-36 2.4062e-38
[torch.FloatTensor of size 4x2x3]4x2x3的张量y由4个2x3的矩阵构成。
torch.tensor与numpy.array的转换
import torch
import numpy as np
np_data = np.arange(6).reshape((2, 3))
torch_data = torch.from_numpy(np_data)##将numpy.array转成torch.tensor
tensor2array = torch_data.numpy()## 将torch.tensort转成numpy.array
print torch_data
print tensor2array,type(tensor2array)
0 1 2
3 4 5
[torch.LongTensor of size 2x3]
[[0 1 2]
[3 4 5]]
<type 'numpy.ndarray'>pytorch中的一些数学运算
# abs 绝对值计算
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
print(
'\nabs',
'\nnumpy: ', np.abs(data), # [1 2 1 2]
'\ntorch: ', torch.abs(tensor) # [1 2 1 2]
)
# sin 三角函数 sin
print(
'\nsin',
'\nnumpy: ', np.sin(data), # [-0.84147098 -0.90929743 0.84147098 0.90929743]
'\ntorch: ', torch.sin(tensor) # [-0.8415 -0.9093 0.8415 0.9093]
)
# mean 均值
print(
'\nmean',
'\nnumpy: ', np.mean(data), # 0.0
'\ntorch: ', torch.mean(tensor) # 0.0
)
矩阵运算:
# matrix multiplication 矩阵点乘
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
# correct method
print(
'\nmatrix multiplication (matmul)',
'\nnumpy: ', np.matmul(data, data), # [[7, 10], [15, 22]]
'\ntorch: ', torch.mm(tensor, tensor) # [[7, 10], [15, 22]]
)
# !!!! 下面是错误的方法 !!!!
data = np.array(data)
print(
'\nmatrix multiplication (dot)',
'\nnumpy: ', data.dot(data), # [[7, 10], [15, 22]] 在numpy 中可行
'\ntorch: ', tensor.dot(tensor) # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0
)
矩阵加法:
import torch
import numpy as np
a=torch.rand(5,3)
b=torch.rand(5,3)
print "a",a
print "b",b
print "a+b",a+b
print "torch.add(a,b)",torch.add(a,b)
res=torch.Tensor(5,3)
print "torch.add(a,b,out=res)",torch.add(a,b,out=res)##把运算结果存储到res上
print "b.add_(a)",b.add_(a)##结果覆盖b
a
0.0540 0.2670 0.6704
0.7695 0.9178 0.8770
0.6552 0.4423 0.1735
0.1376 0.1208 0.6674
0.7257 0.1426 0.1134
[torch.FloatTensor of size 5x3]
b
0.4811 0.7744 0.7762
0.5247 0.6045 0.6148
0.8366 0.8996 0.5378
0.5236 0.4987 0.9592
0.8462 0.8286 0.5010
[torch.FloatTensor of size 5x3]
a+b
0.5350 1.0413 1.4466
1.2942 1.5223 1.4918
1.4918 1.3419 0.7113
0.6612 0.6195 1.6266
1.5719 0.9712 0.6144
[torch.FloatTensor of size 5x3]
torch.add(a,b)
0.5350 1.0413 1.4466
1.2942 1.5223 1.4918
1.4918 1.3419 0.7113
0.6612 0.6195 1.6266
1.5719 0.9712 0.6144
[torch.FloatTensor of size 5x3]
torch.add(a,b,out=res)
0.5350 1.0413 1.4466
1.2942 1.5223 1.4918
1.4918 1.3419 0.7113
0.6612 0.6195 1.6266
1.5719 0.9712 0.6144
[torch.FloatTensor of size 5x3]
b.add_(a)
0.5350 1.0413 1.4466
1.2942 1.5223 1.4918
1.4918 1.3419 0.7113
0.6612 0.6195 1.6266
1.5719 0.9712 0.6144
[torch.FloatTensor of size 5x3]
Tensor的部分截取和numpy里面的切片很类似,操作几乎一样。
autograd自动微分
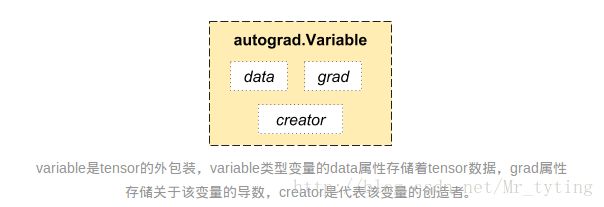
Variable:
我们把每个张量Tensor理解为鸡蛋,那么Variable就是存放这些鸡蛋(torch.Tensor)的篮子。
import torch
from torch.autograd import Variable # torch 中 Variable 模块
# 先生鸡蛋
tensor = torch.FloatTensor([[1,2],[3,4]])
# 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor, requires_grad=True)
print(tensor)
"""
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable)
"""
Variable containing:
1 2
3 4
[torch.FloatTensor of size 2x2]Variable 计算, 梯度
Variable用来包裹tensor, 用Variable代替包住的tensor来进行一系列的运算 , 它在背景幕布后面一步步默默地搭建着一个庞大的系统, 叫做计算图, computational graph. 这个图是用来干嘛的? 原来是将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来。
import torch
import numpy as np
from torch.autograd import Variable
x=Variable(torch.ones(2),requires_grad=True)##用Variable包住一个(2*1)的tensor,并且设置requires_grad=True参与误差反向传播, 要计算梯度
z=4*x*x
y=z.norm()
print "y:",y
y.backward()## 反向计算
print "x.grad:",x.grad##计算y对x的梯度
打印输出
y: Variable containing:
5.6569
[torch.FloatTensor of size 1]
x.grad: Variable containing:
5.6569
5.6569
[torch.FloatTensor of size 2]需要注意:autograd是专门为了BP算法设计的,所以这autograd只对输出值为标量的有用,因为损失函数的输出是一个标量。如果y是一个向量,那么backward()函数就会失效。
autograd的内部机理:
之所以可以实现autograd多亏了Variable和Function这两种数据类型的功劳。要进行autograd必需先将tensor数据包成Variable。Varibale和tensor基本一致,所区别在于多了下面几个属性。
其中data属性返回Variable里面包裹的原始tensor值,就可以将一个Variable类型转换成tensor类型;grad属性返回其梯度值。
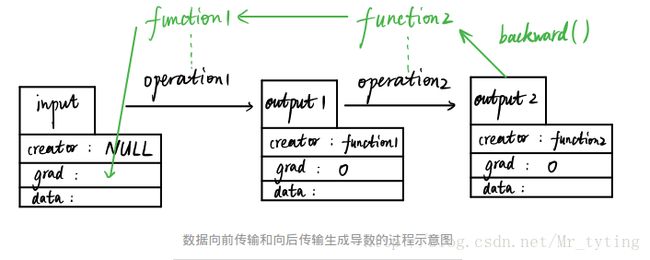
variable和function它们是彼此不分开的:
如图,假设我们有一个输入变量input(数据类型为Variable)input是用户输入的,所以其创造者creator为null值,input经过第一个数据操作operation1(比如加减乘除运算)得到output1变量(数据类型仍为Variable),这个过程中会自动生成一个function1的变量(数据类型为Function的一个实例),而output1的创造者就是这个function1。随后,output1再经过一个数据操作生成output2,这个过程也会生成另外一个实例function2,output2的创造者creator为function2。
在这个向前传播的过程中,function1和function2记录了数据input的所有操作历史,当output2运行其backward函数时,会使得function2和function1自动反向计算input的导数值并存储在grad属性中。
creator为null的变量才能被返回导数,比如input,若把整个操作流看成是一张图(Graph),那么像input这种creator为null的被称之为图的叶子(graph leaf)。而creator非null的变量比如output1和output2,是不能被返回导数的,它们的grad均为0。所以只有叶子节点才能被autograd。
获取 Variable 里面的数据
print(variable) # Variable 形式
"""
Variable containing:
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable.data) # tensor 形式
"""
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable.data.numpy()) # numpy 形式
"""
[[ 1. 2.]
[ 3. 4.]]激励函数
import torch
import torch.nn.functional as F # 激励函数都在这
from torch.autograd import Variable
# 做一些假数据来观看图像
x = torch.linspace(-5, 5, 200) # x data (tensor), shape=(100, 1)
x = Variable(x)
x_np = x.data.numpy() # 换成 numpy array, 出图时用
# 几种常用的 激励函数
y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()
# y_softmax = F.softmax(x) softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类批训练
DataLoader 是 torch 给你用来包装你的数据的工具. 将 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中。使用 DataLoader 有什么好处呢? 就是他们帮你有效地迭代数据。
import torch
import torch.utils.data as Data
torch.manual_seed(1) # reproducible
BATCH_SIZE = 5 # 批训练的数据个数
x = torch.linspace(1, 10, 10) # x data (torch tensor)
y = torch.linspace(10, 1, 10) # y data (torch tensor)
# 先转换成 torch 能识别的 Dataset
torch_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y)
# 把 dataset 放入 DataLoader
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=BATCH_SIZE, # mini batch size
shuffle=True, # 要不要打乱数据 (打乱比较好)
num_workers=2, # 多线程来读数据
)
for epoch in range(3): # 训练所有!整套!数据 3 次
for step, (batch_x, batch_y) in enumerate(loader): # 每一步 loader 释放一小批数据用来学习
# 假设这里就是你训练的地方...
# 打出来一些数据
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())在神经网络里面输出值和输入值都是Variable类型
利用pytorch实现回归拟合
创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它。
#coding:utf-8
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import torch.nn.functional as F
x=torch.unsqueeze(torch.linspace(-1,1,100),dim=1)##torch.unsqueeze返回一个新的tensor,并且在1位置处添加一个新的维度,返回一个shape为(100,1)的tensor
y=x.pow(2)+0.2*torch.rand(x.size()) ##对y添加一点噪音
x,y=Variable(x),Variable(y) ##用Variabvle包裹tensor方便以后求梯度,而且神经网络只能接受Variable类型数据
class Net(torch.nn.Module):
def __init__(self,n_feature,n_hidden,n_output):##自定义各种层结构
super(Net,self).__init__()
self.hidden=torch.nn.Linear(n_feature,n_hidden)
self.predict=torch.nn.Linear(n_hidden,n_output)
def forward(self, x): ##搭建起神经网络
x=F.relu(self.hidden(x)) ##x到达hiddenlayer并且经过relu激活
x=self.predict(x)##x到达输出层,输出层不需要激活,因为回归问题中预测值大小没有区间限制,如果用激活层那么会截断一部分。
return x
##在神经网络里面输出值和输入值都是Variable类型
net=Net(n_feature=1,n_hidden=10,n_output=1)
print net
optimizer=torch.optim.Adam(net.parameters(),lr=0.2) # 传入 net 的所有参数, 学习率
loss_func=torch.nn.MSELoss()# 预测值和真实值的误差计算公式 (均方差)
plt.ion()
plt.show()
for t in range(100):
prediction=net(x)# 喂给 net 训练数据 x, 输出预测值
loss=loss_func(prediction,y) # 计算两者的误差
optimizer.zero_grad()# 清空上一次反向更新所有参数时的残留的参数梯度,因为每次在反向更新参数(BP算法)时,都会保留上一次每个参数的梯度
loss.backward() ##根据误差计算出每个参数的梯度
optimizer.step() # 以学习效率lr=0.2来更新参数,w=w-lr*alpha(loss)/alpha(w)
if t%5 == 0:
plt.cla()##动态画图时,每次画出新的图时,擦除上一时刻画出的图。
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),prediction.data.numpy(),'r-',lw=5)
plt.pause(0.5)利用pytorch实现分类
#coding:utf-8
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torch.nn as nn
n_data=torch.ones(100,2)##返回shape为(100,2)的全1张量
x0=torch.normal(2*n_data,1)##返回hape为(100,2)的张量,并且每个元素都是从均值为2,方差为1的正态分布中随机获取。
y0=torch.zeros(100)##返回shape为(100,1)的全0张量
x1=torch.normal(-2*n_data,1)
y1=torch.ones(100)
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x=torch.cat((x0,x1),0).type(torch.FloatTensor)# FloatTensor = 32-bit floating,dim=0表示在行的方向进行连接
y=torch.cat((y0,y1),).type(torch.LongTensor)# LongTensor = 64-bit integer,注意在pytorch分类问题中,标签默认的要设置为LongTensor类型
x,y=Variable(x),Variable(y)##将X,y tensor用Variable包裹起来,然后放进神经网络里面
class Net(torch.nn.Module):
def __init__(self,n_feature,n_hidden,n_output):
super(Net,self).__init__()
self.hidden=torch.nn.Linear(n_feature,n_hidden)
self.predict=torch.nn.Linear(n_hidden,n_output)
def forward(self, x):
x=F.relu(self.hidden(x))
x=self.predict(x)
return x
net=Net(n_feature=2,n_hidden=10,n_output=2)
print net
optimizer=torch.optim.Adam(net.parameters(),lr=0.01)# 传入 net 的所有参数, 学习率
loss_func=nn.CrossEntropyLoss()# 预测值和真实值的误差计算公式 (交叉熵)
plt.ion()
plt.show()
##在神经网络里面输出值和输入值都是Variable类型
for t in range(100):
out=net(x)
loss=loss_func(out,y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t%2==0:
plt.cla()
#F.softmax(out)得出二维的概率值,是个Variavle类型,1表示在列这个维度上得出每行的最大值,返回最大值和在这个行上的位置index local
prediction=torch.max(F.softmax(out),1)[1]
pred_y=prediction.data.numpy().squeeze()##.data先将Variable类型转成tensor;.numpy再转成numpy.array类型。
##squeeze是将多维数据压缩后仅剩1维,那么这里面为什么要加squeeze()呢?
## 因为下边要计算accuracy=sum(pred_y==target_y)/float(200),那么pred_y和target_y要在格式上对齐
## target_y的shape为(200,)而prediction.data.numpy()的shape为(200,1)
target_y=y.data.numpy()
plt.scatter(x.data.numpy()[:,0],x.data.numpy()[:,1],c=pred_y,s=100,lw=0,cmap='RdYlGn')
accuracy=sum(pred_y==target_y)/float(200)
print "accuracy:",accuracy
plt.pause(0.2)
plt.ioff()
plt.show()利用pytorch实现卷积神经网络(CNN)
#coding:utf-8
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import torch.nn as nn
import torchvision
import matplotlib.pyplot as plt
torch.manual_seed(1)
Epoche=1
Batch_size=50
LR=0.001
Download_mnist=False
train_data=torchvision.datasets.MNIST(
root='./mnist/',
train=True,
transform=torchvision.transforms.ToTensor(),##将numpy.array转成tensor类型,并且将每个像素点从(0-255)压缩到(0-1)
download=Download_mnist
)
torchvision.datasets
print train_data.train_data.size()
print train_data.train_labels.size()
print type(train_data)
train_loader=torch.utils.data.DataLoader(dataset=train_data,batch_size=Batch_size,shuffle=True)
test_data=torchvision.datasets.MNIST(
root='./mnist/',
train=False,
download=True,
transform=torchvision.transforms.ToTensor()
)
#test_x=Variable(torch.unsqueeze(test_data.test_data,dim=1),volatile=True).type(torch.FloatTensor)[:20000]/255
print 'test_data:',test_data.test_data.size() #(10000L, 28L, 28L) (batch_szie,width,height)
test=torch.unsqueeze(test_data.test_data,dim=1)
print 'test:',test.size() #转成下面定义的神经网络输入格式,输入格式(10000L, 1L, 28L, 28L) (batch_size,in_channel,width,height)
test_x=Variable(test,volatile=True).type(torch.FloatTensor)[:20000]
test_y=test_data.test_labels[:20000]
class CNN(nn.Module):
def __init__(self):
super(CNN,self).__init__()
self.conv1=nn.Sequential( #input shape(1,28,28) 此时不考虑batch_size
nn.Conv2d(
in_channels=1,#输入的通道数目,这里只有一个通道
out_channels=16,##输出16张特征图,
kernel_size=5,##卷积核5×5
stride=1,#每次移动的步长1
padding=2,##padding=(kernel_size-stride)/2
), ##output shape(16,28,28)
nn.ReLU(),
nn.MaxPool2d(kernel_size=2), #output shape(16,14,14)
)
self.conv2=nn.Sequential(
nn.Conv2d(16,32,5,1,2), ##output shape(32,14,14)
nn.ReLU(),
nn.MaxPool2d(kernel_size=2), ##output shape(32,7,7)
)
self.out=nn.Linear(32*7*7,10)
def forward(self,x):
x=self.conv1(x)
x=self.conv2(x)
x=x.view(x.size(0),-1) ##x此时的shape(batch_size,32,7,7),x.size(0)=batch_size,x.view将其变为(batch_size,32*7*7)
output=self.out(x)## 上面一步x.view将(batch_size,32,7,7)-->(batch_size,32*7*7),32*7*7的格式满足out输入格式。
return output
cnn=CNN()
print cnn
optimizer=torch.optim.Adam(cnn.parameters(),lr=LR)
loss_func=nn.CrossEntropyLoss()
## 神经网络里面的输入值和输出值都必须是Variable类型
for epoch in range(Epoche):
for step,(x,y) in enumerate(train_loader):
b_x=Variable(x)
b_y=Variable(y)
output=cnn(b_x)
optimizer.zero_grad()
loss=loss_func(output,b_y)
loss.backward()
optimizer.step()
if step%50==0:
test_output=cnn(test_x)
pred_y=torch.max(test_output,1)[1].data.squeeze()
accuracy=sum(pred_y==test_y)/float(test_y.size(0))
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data[0], '| test accuracy: %.2f' % accuracy)
test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')