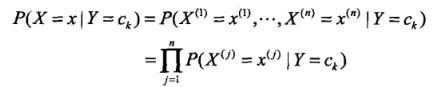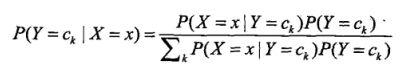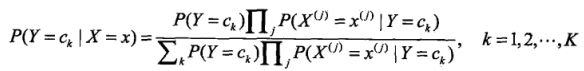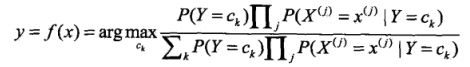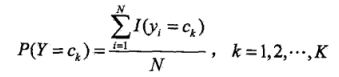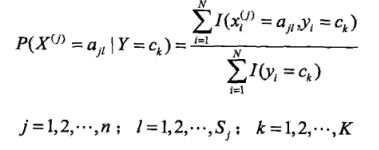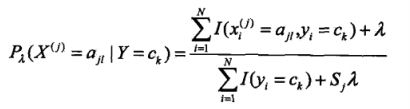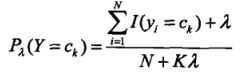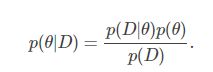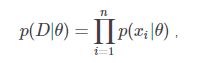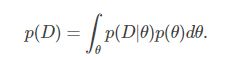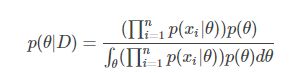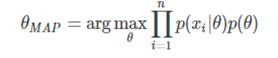朴素贝叶斯_统计学习方法_学习笔记
- 前言
判别学习算法（Discriminative Learning Algorithms）的思路在于直接对于 
进行建模，建模得到的结果可直接来进行分类与预测，如逻辑回归和线性回归。而生成学习算法（Generative Learning Algorithms）的思路在于对y和x的联合概率分布
进行建模，具体方式是通过对于
和
进行建模，结合贝叶斯公式，以后验概率的形式推导出 。由于生成学习算法建模的思路里将数据生成的过程“模拟了一遍”，因此生成学习算法的名头由此而来。高斯判别分析和朴素贝叶斯都是常用的生成学习算法。
朴素贝叶斯（Naive Bayes）是一种常用的生成学习算法。此章介绍的朴素贝叶斯作为解决分类问题而被提出。朴素贝叶斯做了一个较强的假设：各个特征之间条件独立，因此“朴素”一词由此而来。朴素贝叶斯简单易实现，在实际应用中使用广泛，虽然做了一个较强的假设使得结果精度会有所下降，但是实际上精度也是在可以接受的范围之内。
为了加深理解，除了朴素贝叶斯的内容，我将极大似然估计和贝叶斯估计的思想也总结于最后一节。
目录
1 朴素贝叶斯模型与分类问题
1.1 思想
1.2 参数估计
2 拓展
2.1 极大似然估计
2.2 贝叶斯估计
3 小结
1 朴素贝叶斯模型与分类问题
1.1 思想
生成学习算法的思路在于对和进行建模，后通过贝叶斯公式以后验概率的形式计算得到。
假设存在训练数据集：
我们要解决的是一个多分类问题，因此可将先验分布Y写作如下形式：
那么条件概率分布如下所示：
对于上述条件分布而言，直接进行参数估计是不可行的，计算复杂度相当的大。因此为了解决此问题，朴素贝叶斯提出了一个较强的假设：各个特征条件独立（注意与独立相区别）。由此条件独立假设，可将上述条件条件分布拆开写作如下形式：
我们以每一类的后验概率作为判断分类的依据，按照贝叶斯公式，类别为 
的后验概率可写作如下形式：
将朴素贝叶斯假设带入后验概率，可得：
这是朴素贝叶斯分类的基本公式，于是，可将朴素贝叶斯分类器表示为：
注意到，对于每一类的后验概率，分母都是一样的，因此为了减少计算，分类器只需比较分子即可：
由上述分类器进行分析，不难得到，朴素贝叶斯将实例分到后验概率最大的一类，这其实就等价于期望风险最小化，即使分类错误的概率最小化。
1.2 参数估计
当对 建模为广义伯努利分布，对每一个 
同样也建模为广义伯努利分布时，利用最大似然估计不难得到对于参数估计的结果。即先验概率
的参数估计结果如下所示。其中N代表样本的数量。
设第j个特征 
可能取值的集合为
，那么对于条件概率的估计结果为：
看上去似乎并没有什么问题，极大似然的结果也在想象的情况之内。但是当的可能取值并没有在样本中出现时，利用极大似然估计法进行估计，便会将该条件概率估计为0。因为按照最大似然估计的思想，出现次数越多则概率越大，没有出现则概率为0。然而实际情况下，样本数据没有出现并不代表着其不存在。那么当有新的待分类样本中存在着特征并没有在样本数据集中出现的某个取值时，利用上一小节中的分类器进行分类便会出现错误（因为分子分母都为0）。具体例子请见我的其他笔记：斯坦福CS229--生成学习算法。
因此，此时我们可以不采取极大似然进行参数估计，而采取贝叶斯估计法进行参数估计（这里请注意，由于本节涉及到多个贝叶斯，注意区分每一个贝叶斯代表的意义）。贝叶斯估计法进行条件概率的参数估计如下所示。其中
作为参数，常取 
， 
代表特征
有个取值。
直观上看，贝叶斯估计也就是假设每个特征的每种取值都至少出现了 次。即通过这样的先验假设防止了样本中数据的某一特征的某个取值为0的情况。当时，也称为拉普拉斯平滑。
同样，也可以写出先验概率的贝叶斯估计如下所示。其中N代表样本数量，K代表类别的个数。
写到这里，朴素贝叶斯的思想便介绍结束了。可能会对于极大似然估计和贝叶斯估计产生一些疑惑，为了加深理解，我想把极大似然估计和贝叶斯估计做一个比较与分析。也就是说接下来要阐述的内容与朴素贝叶斯这个算法无关，仅仅是为了进一步加深理解。
2 拓展
在1.2节中，使用贝叶斯估计得到的参数会增加朴素贝叶斯算法的鲁棒性，因此我想将极大似然估计和贝叶斯估计做一个梳理以加深理解。这篇博文写得很好：https://blog.csdn.net/liu1194397014/article/details/52766760，以下内容借鉴了该博客。
首先要明白，当我们对于一个随机变量进行概率分布建模后，模型中会存在着一些参数，极大似然估计和贝叶斯估计都是为了进行参数的估计的方法。假设我们有训练数据集
，以及待估计的参数 
，根据贝叶斯公式，可以写出的后验概率形式如下：
（2.1）
下面从两个角度进行介绍，一是频率学派的观点引出最大似然估计；一是贝叶斯学派的观点引出贝叶斯估计。
2.1 极大似然估计
极大似然估计的思路是：出现得多，那么概率也就越大，那么就越可能是真实情况。
因此，可将问题归结为：求解一个，使得概率最大。
从频率学派的观点出发，认为参数 是本来就存在的一个数，也就是说 是固定不变的，因此
就是一个常数，可以不用理会；又因为既然参数固定，那么 
也已经由数据集所确定，因此也可以不用理会。因此可将（2.1）写作：
。由此，便可将求解问题转化为：
又因为数据集
中每个x的采集是独立同分布的，那么便可将优化问题转为：
（2.2）
接下来便是求解该方程的极大值的问题了。这便是极大似然估计的一般形式。
2.2 贝叶斯估计
但是从贝叶斯学派的观点出发，他们认为参数 并不是一个本来就存在的固定的值；相反，参数 是一个随机变量，而且该随机变量 的分布可根据先验知识进行确定。由于不确定，那么根据全概率公式，将（2.1）分母改写成：
结合上式，并带入（2.2），那么（2.1）式可以写作如下形式：
因此，从贝叶斯学派观点出发，参数 作为一个随机变量，在输入数据集的条件下，应该具备上述的概率分布。那么问题就来了，即使的先验分布已知，上面这个式子实际上也是很难求解的，因为分母涉及到的高维积分是很难进行的。而且进一步说，我们寻求参数 的分布意义也不是很大，因为我们只需要参数 的一个值就够了，而不是要获取其整个分布。
为了解决此问题，贝叶斯估计在结合极大似然估计的思想之上，引出了最大一个后验概率（Maximum A Posterior，MAP）。MAP的思想即为：既然没必要求得参数 的具体分布形式，那么选取参数 的出现概率最大的那个值，作为估计的结果不就行了。借鉴MAP的思路，我们就没必要计算分母了，因为作为每个参数 的比较而言，分母都是一样的。因此便可将贝叶斯估计写作如下形式：
从形式上看，即是在最大似然估计的基础上增加参数 的先验分布作为乘积，但是背后蕴含的思想却是截然不同。
顺便提一句，我们在许多算法中应用的正则化项，其实可以利用MAP进行解释。如L1正则项其实是参数服从于拉普拉斯分布的MAP估计，而L2正则项其实是参数服从于高斯分布的MAP的估计。
3 小结
朴素贝叶斯实际上学习到生成数据的机制，所以属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯变得简洁明了，但有时会牺牲一定的分类准确率。但是在许多的应用场景，朴素贝叶斯虽然简单，仍然取得了不错的分类效果。
为了解决极大似然估计进行参数估计之后可能会带来的计算错误，可以采用一些平滑措施如拉普拉斯平滑进行解决。其实质便是利用贝叶斯估计来代替最大似然估计进行参数估计。
贝叶斯估计需要确定参数的先验分布，且先验分布不同所产生的结果也就不同。而极大似然估计则省去了这一点，带来了计算的便利，因此我们常常见许多算法为了简便起见而采用最大似然估计进行参数的估计。而另一方面，利用MAP可以对于正则化项进行解释，因为MAP相当于对于参数做了一个假设，这也是许多算法的损失函数加上正则化项的原因之一。