Matlab之数据回归分析 --- 最小二乘估计曲线拟合
文章目录
- 1、最小二乘估计的概念
- 2、Matlab直线拟合
- 2.1、直线拟合的数学推导
- 2.2、Matlab代码
- 2.3、绘制效果
- 3、多项式曲线拟合
- 3.1、曲线拟合的数学推导
- 3.2、Matlab代码
- 3.3、绘制效果
1、最小二乘估计的概念
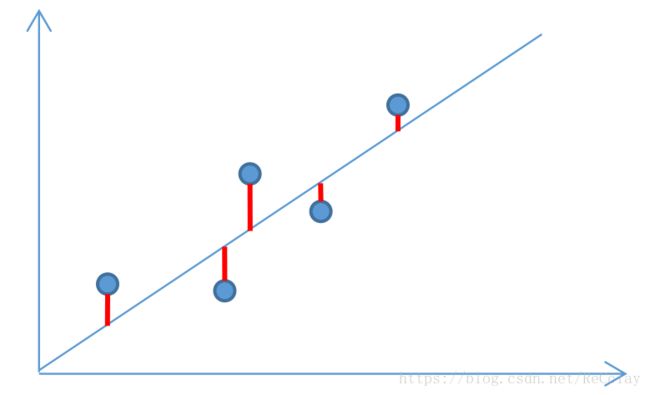
“二乘”意即平方的含义,所以这里也可以称为“最小平方估计”拟合,那么也就有了谁的平方的问题了,直观上理解就是测量值与统计估计值的偏差,工程上又叫残余误差。而“最小”意即所有的残余误差的平方和最小!
通过下图更直观理解,就是让所有红线分别平方,然后求和,所得的值最小!
2、Matlab直线拟合
2.1、直线拟合的数学推导
假设现有一组数据【x1,y1】【x2,y2】…【xn,yn】
设其拟合直线表达式为: (1) y = a + b x y=a+bx\tag{1} y=a+bx(1)
对应残余误差表达式为: (2) d i = y i − ( a + b x i ) d_{i}~ = y_{i} - (a+bx_{i})\tag{2} di =yi−(a+bxi)(2)
最小二乘登场:
(3) D i = ∑ i = 1 n d i 2 = ∑ i = 1 n ( y i − a − b x i ) 2 D_{i}=\sum_{i=1} ^{n} d_{i}^{2} = \sum_{i=1} ^{n}(y_{i}-a-bx_{i})^{2}\tag{3} Di=i=1∑ndi2=i=1∑n(yi−a−bxi)2(3)
因为使得平方和最小,意即求导为0,那么我们就分别对该式子的系数 a 、 b a、b a、b求偏导可得到如下等式:
(4) { ∂ D i ∂ a = ∑ i = 1 n 2 ( y i − a − b x i ) ( − 1 ) = − 2 ( ∑ i = 1 n y i − n a − b ∑ i = 1 n x i ) = 0 ∂ D i ∂ b = ∑ i = 1 n 2 ( y i − a − b x i ) ( − x i ) = − 2 ( ∑ i = 1 n x i y i − a ∑ i = 1 n x i − b ∑ i = 1 n x i 2 ) = 0 \begin{cases} \frac {\partial D_{i}} {\partial a} = \sum\limits _{i=1}^{n}2(y_{i}-a-bx_{i})(-1) = -2(\sum\limits _{i=1} ^{n}y_{i}-na-b\sum\limits _{i=1} ^{n} x_{i}) = 0 \\ \\ \frac {\partial D_{i}} {\partial b} = \sum\limits _{i=1}^{n}2(y_{i}-a-bx_{i})(-x_{i}) = -2(\sum\limits _{i=1} ^{n}x_{i}y_{i}-a\sum\limits _{i=1}^{n} x_{i}-b\sum\limits _{i=1} ^{n} x_{i}^2) = 0\tag{4} \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂a∂Di=i=1∑n2(yi−a−bxi)(−1)=−2(i=1∑nyi−na−bi=1∑nxi)=0∂b∂Di=i=1∑n2(yi−a−bxi)(−xi)=−2(i=1∑nxiyi−ai=1∑nxi−bi=1∑nxi2)=0(4)
整理可得,
(5) { ( ∑ i = 1 n y i − n a − b ∑ i = 1 n x i ) = 0 ∑ i = 1 n x i y i − a ∑ i = 1 n x i − b ∑ i = 1 n x i 2 ) = 0 ⟹ { a = y ‾ − b x ‾ b = x y ‾ − x ‾ y ‾ x 2 ‾ − ( x ‾ ) 2 \begin{cases} (\sum \limits_{i=1} ^{n}y_{i}-na-b\sum\limits _{i=1} ^{n} x_{i}) = 0 \\ \\ \sum\limits _{i=1} ^{n}x_{i}y_{i}-a\sum\limits _{i=1}^{n} x_{i}-b\sum\limits _{i=1} ^{n} x_{i}^2) = 0 \end{cases}\Longrightarrow \begin{cases} a=\overline{y}-b\overline{x} \\ \\ b=\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{x^2}-(\overline{x})^2} \end{cases}\tag{5} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧(i=1∑nyi−na−bi=1∑nxi)=0i=1∑nxiyi−ai=1∑nxi−bi=1∑nxi2)=0⟹⎩⎪⎨⎪⎧a=y−bxb=x2−(x)2xy−xy(5)
2.2、Matlab代码
clc;
clear;
%录入X轴数据
for a = 1:30
x(a) = a-1;
end
%录入Y轴数据
y=[1,2,3,8,6,9,5,4,8,5,9,19,16,12,15,24,22,36,40,40,32,32,36,39,52,52,56,57,62,69];
figure;
plot(x,y,'.');%画点
hold on
b = ( mean(x*y(:)) - mean(x(:)).*mean(y(:)) ) / (mean(x*x(:))-mean(x(:))^2 );
a = mean(y(:)) - b*mean(x(:));
y1 = a+b*x;
plot(x,y1);
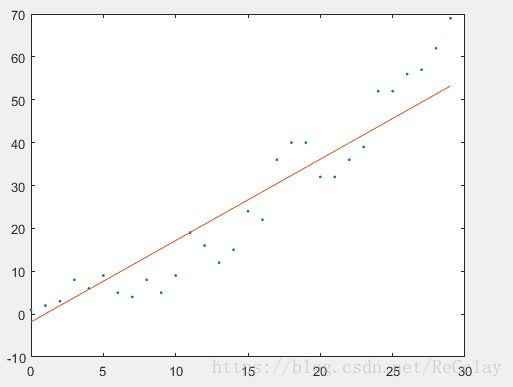
2.3、绘制效果
3、多项式曲线拟合
3.1、曲线拟合的数学推导
同时,假设有一组数据【x1,y1】【x2,y2】…【xn,yn】
设拟合多项式表达式为:
(1) y = a + a 1 x + . . . + a k x k y=a+a_{1}x+...+a_{k}x^{k}\tag{1} y=a+a1x+...+akxk(1)
残余误差和表达式为:
(2) D 2 = ∑ i = 1 n [ y i − ( a 0 + a 1 x i + . . . + a k + x i k ) ] 2 D^{2}=\sum_{i=1}^{n}[y_{i}-(a_{0}+a_{1}x_{i}+...+a_{k}+x_{i}^{k})]^{2}\tag{2} D2=i=1∑n[yi−(a0+a1xi+...+ak+xik)]2(2)
为求平方和最小,我们只需对系数 a 0 a k a_{0}~a_{k} a0 ak挨个求偏导,即可得到:
(3) { − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + . . . + a k x i k ) ] = 0 − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + . . . + a k x i k ) ] x i = 0 . . . . . . − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + . . . + a k x i k ) ] x i k = 0 \begin{cases} -2\sum\limits _{i=1}^{n}[y_{i}-(a_{0}+a_{1}x_{i}+...+a_{k}x_{i}^{k})] = 0 \\ -2\sum\limits _{i=1}^{n}[y_{i}-(a_{0}+a_{1}x_{i}+...+a_{k}x_{i}^{k})]x_{i} = 0\\ ......\\ -2\sum\limits _{i=1}^{n}[y_{i}-(a_{0}+a_{1}x_{i}+...+a_{k}x_{i}^{k})]x_{i}^{k} = 0 \end{cases}\tag{3} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧−2i=1∑n[yi−(a0+a1xi+...+akxik)]=0−2i=1∑n[yi−(a0+a1xi+...+akxik)]xi=0......−2i=1∑n[yi−(a0+a1xi+...+akxik)]xik=0(3)
上述等式继续化简可得:
(4) { a 0 n + a 1 ∑ i = 1 n x i + . . . + a k ∑ i = 1 n x i k = ∑ i = 1 n x i 0 y i a 0 ∑ i = 1 n x i + a 1 ∑ i = 1 n x i 2 + . . . + a k ∑ i = 1 n x i k + 1 = ∑ i = 1 n x i 1 y i . . . a 0 ∑ i = 1 n x i k + a 1 ∑ i = 1 n x i k + 1 + . . . + a k ∑ i = 1 n x i 2 k = ∑ i = 1 n x i k y i \begin{cases} a_{0}n+a_{1}\sum\limits_{i=1}^{n}x_{i}+...+a_{k}\sum\limits _{i=1}^{n}x_{i}^{k}=\sum\limits _{i=1}^{n}x_{i}^{0}y_{i}\\ a_{0}\sum\limits_{i=1}^{n}x_{i}+a_{1}\sum\limits_{i=1}^{n}x_{i}^{2}+...+a_{k}\sum\limits_{i=1}^{n}x_{i}^{k+1}=\sum\limits_{i=1}^{n}x_{i}^{1}y_{i}\\ ...\\ a_{0}\sum\limits_{i=1}^{n}x_{i}^{k}+a_{1}\sum\limits_{i=1}^{n}x_{i}^{k+1}+...+a_{k}\sum\limits_{i=1}^{n}x_{i}^{2k}=\sum\limits_{i=1}^{n}x_{i}^{k}y_{i} \end{cases}\tag{4} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧a0n+a1i=1∑nxi+...+aki=1∑nxik=i=1∑nxi0yia0i=1∑nxi+a1i=1∑nxi2+...+aki=1∑nxik+1=i=1∑nxi1yi...a0i=1∑nxik+a1i=1∑nxik+1+...+aki=1∑nxi2k=i=1∑nxikyi(4)
将这些等式表达成矩阵的形式,可以得到如下矩阵:
(5) [ n ∑ i = 1 n x i ⋯ ∑ i = 1 n x i k ∑ i = 1 n x i ∑ i = 1 n x i 2 ⋯ ∑ i = 1 n x i k + 1 ⋮ ⋮ ⋱ ⋮ ∑ i = 1 n x k ∑ i = 1 n x i k + 1 ⋯ ∑ i = 1 n x i 2 k ] [ a 0 a 1 ⋮ a k ] = [ ∑ i = 1 n y i ∑ i = 1 n x i y i ⋮ ∑ i = 1 n x i k y i ] \begin{bmatrix} n & \sum\limits_{i=1}^{n}x_{i} & \cdots & \sum\limits_{i=1}^{n}x_{i}^{k} \\ \sum\limits_{i=1}^{n}x_{i} & \sum\limits_{i=1}^{n}x_{i}^{2} & \cdots & \sum\limits_{i=1}^{n}x_{i}^{k+1} \\ \vdots & \vdots & \ddots & \vdots \\ \sum\limits_{i=1}^{n}x_{k} & \sum\limits_{i=1}^{n}x_{i}^{k+1} & \cdots & \sum\limits_{i=1}^{n}x_{i}^{2k} \\ \end{bmatrix} \begin{bmatrix} a_{0}\\a_{1}\\ \vdots \\ a_{k} \end{bmatrix}= \begin{bmatrix} \sum\limits_{i=1}^{n}y_{i} \\ \sum\limits_{i=1}^{n}x_{i}y_{i} \\ \vdots \\ \sum\limits_{i=1}^{n}x_{i}^{k}y_{i} \end{bmatrix} \tag{5} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡ni=1∑nxi⋮i=1∑nxki=1∑nxii=1∑nxi2⋮i=1∑nxik+1⋯⋯⋱⋯i=1∑nxiki=1∑nxik+1⋮i=1∑nxi2k⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎡a0a1⋮ak⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡i=1∑nyii=1∑nxiyi⋮i=1∑nxikyi⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤(5)
然后接着将这个范德蒙德行列式化简,可以得到:
(6) [ 1 x 1 ⋯ x 1 k 1 x 2 ⋯ x 2 k ⋮ ⋮ ⋱ ⋮ 1 x n ⋯ x n k ] [ a 0 a 1 ⋮ a k ] = [ y 1 y 2 ⋮ y n ] \begin{bmatrix} 1 & x_{1} & \cdots & x_{1}^{k} \\ 1 & x_{2} & \cdots &x_{2}^{k} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & \cdots & x_{n}^{k} \\ \end{bmatrix} \begin{bmatrix} a_{0}\\a_{1}\\ \vdots \\ a_{k} \end{bmatrix}= \begin{bmatrix} y_{1}\\y_{2}\\ \vdots \\ y_{n} \end{bmatrix} \tag{6} ⎣⎢⎢⎢⎡11⋮1x1x2⋮xn⋯⋯⋱⋯x1kx2k⋮xnk⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡a0a1⋮ak⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤(6)
接着我们的分析 X A = Y XA=Y XA=Y,那么 A = X − 1 Y A=X^{-1}Y A=X−1Y。由于这里需求 X X X的逆矩阵,求逆矩阵的前提是满秩,但是这里可能没有办法满足这一点,所以我们利用广义矩阵可以得到, A = ( X T ∗ X ) − 1 ∗ X T ∗ Y A=(X^{T}*X)^{-1}*X^{T}*Y A=(XT∗X)−1∗XT∗Y,这样便得到了系数矩阵 A A A,我们也就进一步得到了拟合曲线。
3.2、Matlab代码
clc;
clear;
%录入X轴数据
for a = 1:30
x(a) = a-1;
end
%录入Y轴数据
y=[1,2,3,6,6,7,8,9,8,10,9,19,16,14,15,24,28,36,40,40,42,41,37,39,52,52,56,57,62,69];
figure
plot(x,y,'.');%画点
hold on
k=5;%阶数 阶数可以在1-5之间更改看效果,记得每次更改了之后clear workspace然后在运行
%X数据录入
for a = 0:k
for i = 1:30
X(i,(a+1)) = x(i).^(a);
end
end
Y = y';
A = (X'*X)^-1*X'*Y;%求矩阵系数A
A = A';%转置矩阵方便使用
z = 0:0.1:30;
if k==5
y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3+A(5).*z.^4+A(6).*z.^5;%最后表达式用于绘图
elseif k==4
y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3+A(5).*z.^4;%最后表达式用于绘图
elseif k==3
y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3;%最后表达式用于绘图
elseif k==2
y1 = A(1)+A(2).*z+A(3).*z.^2;%最后表达式用于绘图
elseif k==1
y1 = A(1)+A(2).*z;%最后表达式用于绘图
end
plot(z,y1);
hold off
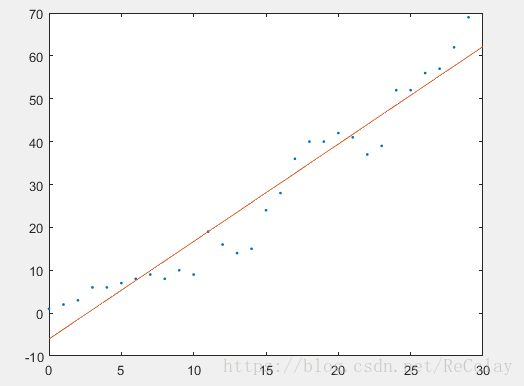
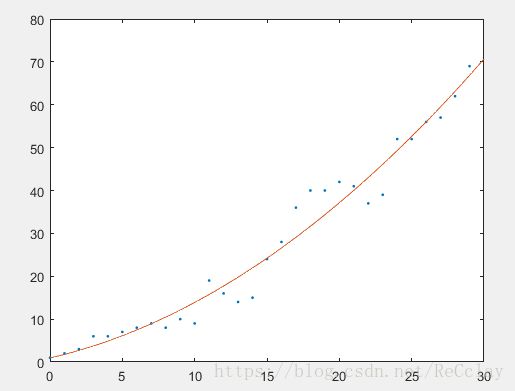
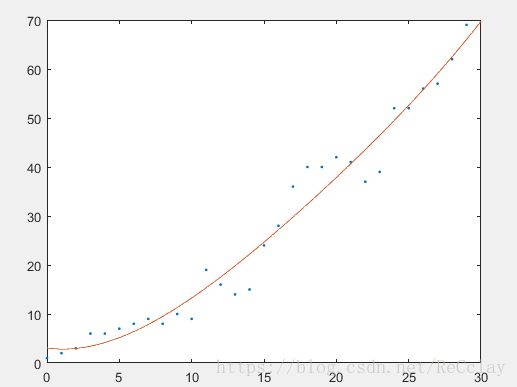
3.3、绘制效果
k=1