记录:成像与坐标系转换
这里是我在对Kinect标定参数时发现的一些可能会导致像我一样的初学者犯下的错误以及误区,所以在这里mark一下。如果有错误的地方,希望能在评论区解释一下,感激不尽。
首次简单介绍一下后面操作需要用到的Kinect设备的参数:
Kinect的视角场(FOV)—垂直方向43度,水平方向57度,整体的三维模型为“金字塔”形状。最大深度4m,最小深度0.6m。
下面介绍一下这篇文章需要先了解的一些基础知识:
1.由于光沿直线传播,所以对于远近不一的物体,人眼可以看到这些物体表现为在一个平面上。
2.图像坐标系:是基于图像平面的一种坐标系,默认为以矩形左上角的点为原点,水平向左为x轴的正方向,垂直向下为y轴的正方向。(为了方便后面计算,这里我通过Kinect获得的图像分辨率为640*480)。
3.摄像机坐标系:是以摄像头中心为原点的空间坐标系,就像在“金字塔”形状的空间内,这里默认是以垂直地面向下为y轴正方向,水平面垂直金字塔底面(我通常都假想为一个图像的成像的平面)的方向是z轴的正方向,与z轴,y轴组成平面垂直向右为x轴正方向。
4.坐标系转换:
这里转换后的坐标系坐标用w表示
用M表示辅助矩阵
转换前的坐标系的坐标用c表示
就有 w=Mc
其中,R是3*3的正交单位矩阵,t是三维平移向量,矢量 0⃗ =(0,0,0) ,所以M是一个4*4矩阵
下面进入正题
1.图像坐标系向摄像头坐标系的转换
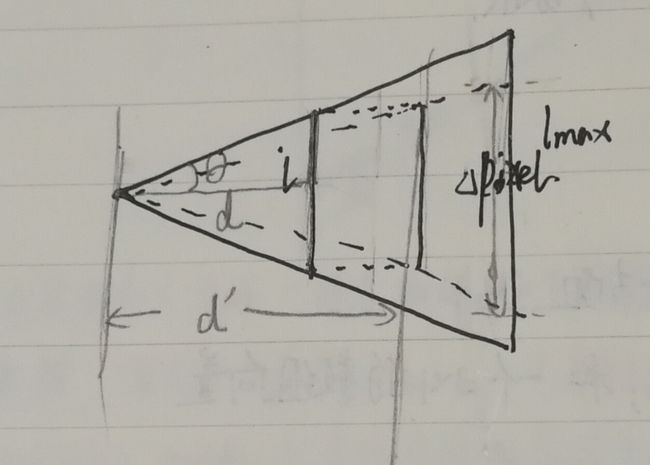
首先,我们需要了解物体成像,尤其是针孔成像的特点,发现对于一个物体的不同深度值,相同长度下 l 对应的像素长度也不同,得出结论,像素转毫米的比例 scale 与深度且仅与深度有关,姑且在计算比例计算时我们可以将视角场中的物体的长度取最长,刚好被包含在视角场内,对于高度 height: lmax−>480pixels ;长度 width: lmax−>640pixels
由相似三角形计算可以得到
所以对于摄像头坐标系中的坐标矩阵向量 c
2.摄像头坐标系向任意空间坐标系的转换
这里必须声明一点,因为在实际测量时,摄像头坐标系的原点是很难精确确定位置的,也就是说如果要获得精确的物体坐标,就必须将坐标系转换到一个具有更容易确定的原点的空间坐标系中。
方法就是使用坐标系转换公式,顺便提一下,这种根据实际测量值进行参数计算的超大计算量的工作,完全可以交由 matlab 去处理(所以学好 matlab 很重要的)
如果以为只要测几组数据处理一下获得一个转换前的矩阵向量和一个转化年后的矩阵向量形成一个方程组求解就可以了,那就大错特错了,在使用 matlab s时就会发现,如果仅仅是将转换前的矩阵向量和转换后的矩阵向量带入,获得的一定是一个最简单的4*1的解(是不是很崩溃),别急,这里需要一个等价思想。
a11x1+a12x2+a13x3+a14x4=y1
a21x1+a22x2+a23x3+a24x4=y2
a31x1+a32x2+a33x3+a34x4=y3
a41x1+a42x2+a43x3+a44x4=y4
这个方程组在 matlab 中的求解只会得到上面说的那种没什么用处的结果,现在如果将每一个方程中的系数作为未知量求解,四组数据作为相应参数,那么得到的4*1的矩阵刚好可以作为 {a11,a12,a13,a14} 的值,此时需要四组数据组成下面的方程组:
x11a11+x12a12+x13a13+x14a14=y1
x21a11+x22a12+x23a13+x24a14=y2
x31a11+x32a12+x33a13+x34a14=y3
x41a11+x42a12+x43a13+x44a14=y4
根据这样的方法就可以分别得到四组解作为原始方程组的四个方程的系数,换句话说,也就是辅助矩阵 M
附:
在标定的过程中会出现很多噪点,导致数据不是很精确,但是由于能力不足,没有去做相应的数据处理,导致出现很致命的问题,最典型的可能就是对于图像中显示的地面,在我的坐标系中应该在y轴的值是大于0的,但是由于不精确的数据所得到的辅助矩阵,会通过第二行(如果仔细看过矩阵乘法以及演算过坐标系转换公式的人可以看得懂为什么说是第二行,这里不再赘述)以外的数据对整个转换后的计算结果(矩阵)产生影响,造成小于0,也就是说在我的原点的上方(试问我怎么会选一个地面以下的一个点去做测量,呵呵);另外就是,验证过程中发现,越靠近地面,我经过转换得到的y值误差越大,这些都是不精确的数据带来的误差。
为什么要说这个失败的历史呢?因为我在发现数据不准的情况下没想过是数据不精确的问题所带来的,而是怀疑过像素转毫米的数学思想的正确性。下面是我对于摄像头成像的错误想法,引以为戒。
在面对物厚度的物体(小纸条,因为我是用小纸条定在卷尺上进行数据采集的)或不能看到厚度(墙面)时,Kinect的成像图片可以准确判断水平方面横坐标距离,当从侧边斜视一个具有一定厚度的物体时,由于成像原理(同一分辨率下,深度越大,单位像素对应的长度越长)以及Kinect深度图像的显示图片原理(平面不可能知道三维空间中厚度,深度,所以看不到的部分,应该是被物体厚度遮住了,呈现黑色即无数据)
所以我认为通过像素转毫米的计算公式,应该是将图像坐标系中的每个点都进行积分,对于离散型的点来说,就是累加,当然,最后的结果错的更加离谱