CNN训练相关细节
#CNN训练相关细节
记录学习CNN结构搭建、训练、模型实现等过程中遇到的问题。更新于2018.10.18。
更多内容,欢迎加入星球讨论。
文章目录
- 超参数确定方法
- 学习率
- Batch Size
- Caffe | Solver / Model Optimization
- 损失计算
- 判断网络是否收敛(Converge)
- Caffe中的神经网络
- Softmax、Softmax Loss和Cross-Entropy Loss
超参数确定方法
在神经网络的训练过程中往往有许多需要确定的超参数(如momentum、batch size、base learning rate、weight_decay等),还需要确定网络的训练次数(既保证了网络已经收敛到一个合适的值,又要防止over-fitting)。因此,我开始查找在网络训练的过程中该如何确定超参数。下面是整理的超参数确定方法,如果以后有用到其中的几种,再来更新使用评价。
ResearchGate上面的一个回答中推荐了Bayesian optimization和Hyperband。回答中也提到许多近期的方法,比如Practical Bayesian Optimization of Machine Learning Algorithms。 其他回答也可以通过随机的方法查找确定超参数。
学习率
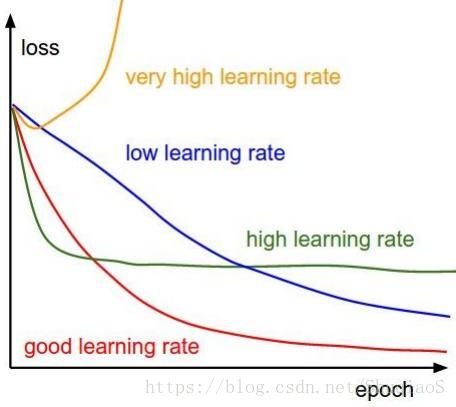
关于学习率的确定,当时学习课程cs231n 的时候,记得吴恩达老师提供的学习率确定方法是通过设置一定间隔的学习率,分别训练并画出训练曲线,从而选择合适的学习率。目前手头有一个正在训练的网络,由于之前有参考的数值,因此就从那个数值(1e-4)开始训练,发现在训练过程中,损失开始下降很快,但后面训练损失出现了明显的波动,因此怀疑是否是学习率过高导致的。同时,交叉验证集的损失也出现了微小的上扬弧度,可能是存在过拟合,此时应当尝试减少训练次数。
这里放一张课程中提到的训练曲线与学习率的关系比较:
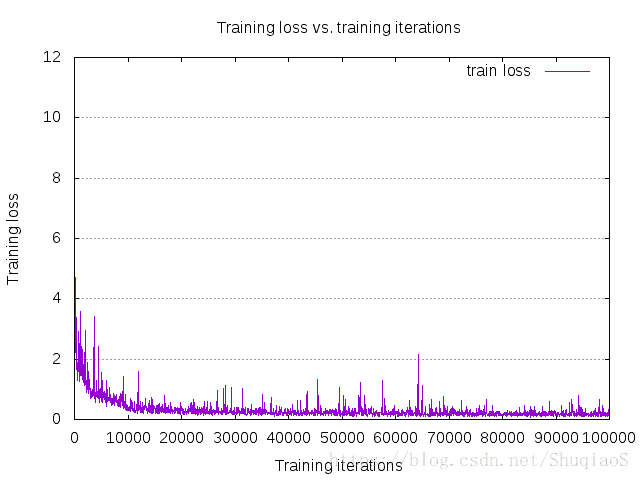
实际应用:
下图是博主在实验中得到的训练曲线。
Batch Size
结论:
一般来说,在合理的范围之内,越大的 batch size 使下降方向越准确,震荡越小;batch size 如果过大,则可能会出现局部最优的情况。小的 bath size 引入的随机性更大,难以达到收敛,极少数情况下可能会效果变好。
具体介绍可以参照原文和其参考文献。
Caffe | Solver / Model Optimization
Caffe Solver有如下几种优化方法:
- Stochastic Gradient Descent (type: “SGD”)
- AdaDelta (type: “AdaDelta”),
- Adaptive Gradient (type: “AdaGrad”),
- Adam (type: “Adam”),
- Nesterov’s Accelerated Gradient (type: “Nesterov”) and
- RMSprop (type: “RMSProp”)
损失计算
对于一个数据库 D D D,所要优化的目标是所有 ∣ D ∣ |D| ∣D∣ 个数据集内样本对应的损失的平均:
L ( W ) = 1 ∣ D ∣ ∑ i ∣ D ∣ f W ( X ( i ) ) + λ r ( W ) L(W)=\dfrac{1}{|D|}\sum_{i}^{|D|}f_W(X^{(i)}) + \lambda r(W) L(W)=∣D∣1∑i∣D∣fW(X(i))+λr(W)
其中 f W ( X i ) f_W(X^{i}) fW(Xi) 是样本 X ( i ) X^{(i)} X(i) 对应的损失, r ( W ) r(W) r(W) 是带有权重的归一化项。但是,在实际应用过程中, ∣ D ∣ |D| ∣D∣ 往往很大,因此用了下面的近似:
L ( W ) ≈ 1 N ∑ i N f W ( X ( i ) ) + λ r ( W ) L(W)\approx\dfrac{1}{N}\sum_{i}^{N}f_W(X^{(i)}) + \lambda r(W) L(W)≈N1∑iNfW(X(i))+λr(W)
其中 N ≫ ∣ D ∣ N\gg|D| N≫∣D∣ 。
模型计算的是前向传播过程中产生的 f W f_W fW,并将 ∇ f W \nabla f_W ∇fW 用于反向传播。参数 ∇ W \nabla W ∇W 的更新依据梯度 ∇ f W \nabla f_W ∇fW、正则项梯度 ∇ r ( W ) \nabla r(W) ∇r(W) 等其他取决于具体优化方法的参数。
例: ADAM
这里以实验过程中常用的Adam优化方法为例。Adam与SGD相似,都是基于梯度的优化方法。Adam中包含了“adaptive moment estimation” ( m t m_t mt, v t v_t vt),更新方式类似于正则化的AdaGrad方法。具体的更新公式如下:
( m t ) i = β 1 ( m t − 1 ) i + ( 1 − β 1 ) ( ∇ L ( W t ) ) i (m_t)_i = \beta_1(m_{t-1})_i + (1-\beta_1)(\nabla L(W_t))_i (mt)i=β1(mt−1)i+(1−β1)(∇L(Wt))i
( v t ) i = β 2 ( m t − 1 ) i + ( 1 − β 2 ) ( ∇ L ( W t ) ) i 2 (v_t)_i = \beta_2(m_{t-1})_i + (1-\beta_2)(\nabla L(W_t))_i^2 (vt)i=β2(mt−1)i+(1−β2)(∇L(Wt))i2
且
( W t − 1 ) i = ( W t ) i − α 1 − ( β 2 ) i t 1 − ( β 1 ) i t ( m t ) i ( v t ) i + ε (W_{t-1})_i = (W_t)_i - \alpha \dfrac {\sqrt{1-(\beta_2)_i^t}}{1-(\beta_1)_i^t} \dfrac{(m_t)_i}{\sqrt{(v_t)_i} + \varepsilon} (Wt−1)i=(Wt)i−α1−(β1)it1−(β2)it(vt)i+ε(mt)i
Adam作者Kingma等人建议的参数取值为: β 1 = 0.9 , β 2 = 0.999 , ε = 1 0 − 8 \beta _ 1 = 0.9, \beta_2 = 0.999, \varepsilon = 10^{-8} β1=0.9,β2=0.999,ε=10−8, 对应Caffe中分别为momemtum、momentum2和delta。在已经实践过的网络中,DispNet用的是0.9、0.999和1e-4。
##训练神经网络
这一部分记录了在训练过程中遇到的问题和存在的困惑。
判断网络是否收敛(Converge)
目前没有方法能够确定地给出神经网络是否已经得到了充分的训练并达到了最优值,但仍可以通过一些手段估计网络是否已经收敛,从而帮助我们在合适的位置停止训练(既得到较好的结果,又尚未发生过拟合)。
其中一个方法是在训练过程中监测训练集和交叉测试集的损失,即画出训练曲线。当训练损失与测试损失都维持在一个相对稳定的状态且二者差距几乎不变时,网络就基本训练好了。剩下的就是根据实际的网络效果判断是否还需要继续训练。
*关于训练曲线:训练曲线往往存在许多波动,许多教程上使用的平滑的训练曲线只是描绘一个趋势,并非真正的训练曲线的样子。
Caffe中的神经网络
Caffe是一个非常强大、简便的深度学习框架,允许使用者用简单的格式化语言快速构建一个神经网络。容易上手,使用方便。
博主在研究过程中也用到了Caffe搭建神经网络,考虑到Caffe内容的复杂性,因此单独将神经网络的构建另写一个博客记录。
Softmax、Softmax Loss和Cross-Entropy Loss
在分类问题中,通常分类器会给出样本对应各类别的概率,我们希望的是选出其中概率最大的那个作为最终判定的类别。然而,对于神经网络而言,由于反向传播需要用到目标函数的微分,可 max \max max运算不可微,这就导致了目标函数无法求导,也就无法反向传播。为了解决这个问题,才出现了Softmax。
Softmax的作用也是找到概率最大的那个类别,只不过变成了可微的形式。不仅如此,经过了Softmax的压缩,所有的样本都在区间 [ 0 , 1 ] [0,1] [0,1]内,且和为1,这也满足概率的形式。Softmax公式为:
f j ( z ) = e z j ∑ k e z k f_j(z)=\frac{e^{z_j}}{\sum_ke^{z_k}} fj(z)=∑kezkezj
其中, z z z为原始的概率输出。
需要注意的是,在SVM分类器中,通常应用hinge loss(有时也称为max-margin loss);而在Softmax分类器中,通常应用cross-entropy loss。这里,Softmax分类器的得名是来源于其应用了Softmax压缩原始输出,此时才可以应用交叉熵损失。技术上,没有一个东西叫"Softmax loss",因为Softmax毕竟只是一个压缩函数,目前通常用它作为一个简称(Softmax+cross-entropy)。
交叉熵损失的形式为:
L i = − log ( e y i f ∑ j e f j ) L_i=-\log\left(\frac{e^f_{y_i}}{\sum_je^{f_j}}\right) Li=−log(∑jefjeyif)
或者也可以等价于:
L i = − f y i + log ∑ j e f j L_i=-f_{y_i}+\log\sum_je^{f_j} Li=−fyi+logj∑efj
其中, f j f_j fj表示分类器的输出 f f f中对应第 j j j个类别的概率。
更多详细信息可以参看CS231n课程。