论文学习(翁荣祥毕业论文)
基础知识
1.存在的问题:双语数据的规模与神经网络的参数规模的不平衡,导致现有的神经机器翻译模型生成的向量表示无法包含有足够语言信息。
2.基于规则的翻译方式->统计机器翻译(步骤如
https://www.cnblogs.com/wuseguang/p/4072920.html
1.语料预处理,生成双语分词之后的文件。2.词对齐。3.短语抽取。4.计算短语概率。5.最大熵调序。)->神经机器翻译。
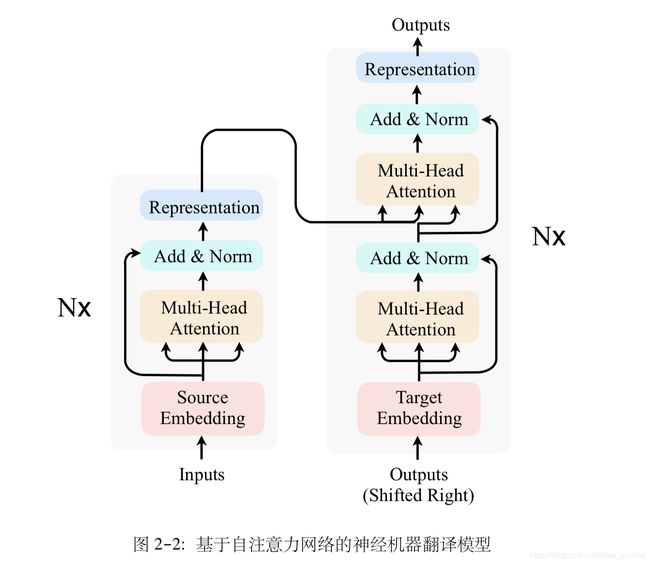
3.神经机器翻译模型结构:
编码器-解码器(常见神经网络:RNN,CNN,SAN(自注意力神经网络(Self-Attention Network)))
基于循环神经网络的神经机器翻译模型:
使⽤⼀个双向循环神经⽹络构成的编码器将给定的源端句⼦的词向量(Word Vector)编码成⼀组向量表⽰并且将这组隐层状态表⽰合成⼀个初始状态(Initial State)输⼊到解码器中,⽽解码器使⽤⼀个单向的循环神经⽹络进⾏逐词解码。这其中每输出⼀个⽬标词之前都会通过注意⼒机制来对源端编码成的状态表⽰进⾏计算,从⽽获取需要输出的⽬标词的在源端的信息。
翻译质量评价:
BlEU:通过计算翻译结果中的N元文法(N-garm)和参考译文中的N元文法的匹配成功率来评估翻译质量。
具体计算方法:
B L E U = B P ∗ e x p ∑ n = 1 N w n l o g p n BLEU=BP*exp\sum^N_{n=1}w_nlogp_n BLEU=BP∗expn=1∑Nwnlogpn
w n w_n wn:n元文法中的重要性?
B P BP BP:长度惩罚因子,避免生成的翻译结果过短。?
B P = { e 1 − r t t ≤ r 1 t > r BP=\{^{1\ \ \ \ \\ \ \ \ \ \ t>r}_{e^{\frac{1-r}{t}\ \ \ \ \ \ \ \ \ t\le{r}}} BP={et1−r t≤r1 t>r
p n = ∑ e ∈ T r a n s l a t i o n ∑ n − g a r m ∈ e C o u n t c l i p ( n − g r a m ) ∑ e ′ ∈ R e f e r a n c e ∑ n − g a r m ∈ e ′ C o u n t ( n − g r a m ) p_n=\frac{\sum_{e\in{Translation}}\sum_{n-garm\in{e}}Count_{clip}(n-gram)}{\sum_{e^{'}\in{Referance}}\sum_{n-garm\in{e^{'}}}Count(n-gram)} pn=∑e′∈Referance∑n−garm∈e′Count(n−gram)∑e∈Translation∑n−garm∈eCountclip(n−gram)
论文提出的方法
1.在神经机器翻译模型中引入词预测机制
论文中认为初始状态对翻译质量影响不大的原因是因为没有显式的建模控制初始状态的生成。
解决方法:提出一种词预测机制,并将其结合到现有的翻译模型中,将目标句子所有的词来作为初始状态生成的约束来控制初始状态;同时扩展词预测机制的使用范围,将其应用到解码器所有隐层状态中,即每个状态除了要生成当前的词,还需要能够预测未来所需翻译的词。
词预测机制
平行句对 x \mathrm{x} x和 y \mathrm{y} y,在编码器把源句编码成舒适状态后,要求这个状态能够一次预测出目标端句子 y \mathrm{y} y的所有词(不需要顺序)
对于解码器的每一时间步j,对应的隐层状态 s j s_j sj需要预测之后的所有词 y j , y j + 1 , . . . , y J y_j,y_{j+1},...,y_J yj,yj+1,...,yJ

词预测机制约束初始状态

词预测机制约束隐层状态

训练函数
通过增加额外的训练函数来控制生成隐层状态,不涉及解码过程,因此引入词预测机制不会减慢模型的翻译速度。
1. W P E 机 制 : L = L t r a n s + L W P E 1.WP_E机制:L=L_{trans}+L_{WP_E} 1.WPE机制:L=Ltrans+LWPE
= 1 J ∑ j = 1 J l o g P ( y j ∣ y < j , x ) + l o g P W P E =\frac{1}{J}\sum^J_{j=1}logP(y_j|y_{<j},\mathrm{x})+logP_{WP_E} =J1j=1∑JlogP(yj∣y<j,x)+logPWPE
2. W P D 机 制 : L = L t r a n s + L W P D 2.WP_D机制:L=L_{trans}+L_{WP_D} 2.WPD机制:L=Ltrans+LWPD
= 1 J ∑ j = 1 J l o g P ( y j ∣ y < j , x ) + ∑ j = 1 J 1 J − j + 1 l o g P W P D =\frac{1}{J}\sum^J_{j=1}logP(y_j|y_{<j},\mathrm{x})+\sum^J_{j=1}\frac{1}{J-j+1}logP_{WP_D} =J1j=1∑JlogP(yj∣y<j,x)+j=1∑JJ−j+11logPWPD
3. W P E + W P D : L = L t r a n s + L W P E L = L t r a n s + L W P E + L W P D 3.WP_E+WP_D:L=L_{trans}+L_{WP_E}L=L_{trans}+L_{WP_E}+L_{WP_D} 3.WPE+WPD:L=Ltrans+LWPEL=Ltrans+LWPE+LWPD
词表是什么?作用?
解码阶段使用词预测器
解码器开始通过初始状态进行解码之前,词预测机制可以对即将生成的词进行预测,然后选出其中概率最大的K个词,作为解码器解码时所需要的新词表。
2.在神经机器翻译中建模句子级全局表示
胶囊网络:
https://blog.csdn.net/godwriter/article/details/79216404
针对CNN忽略了图像的位置信息这一缺点提出的模型。
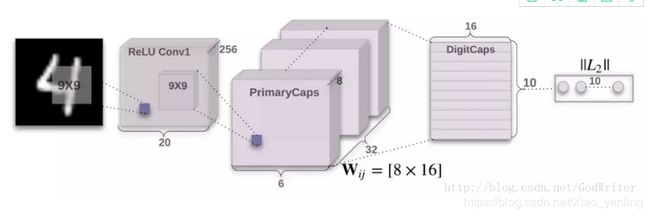

生成句子级全局状态表示
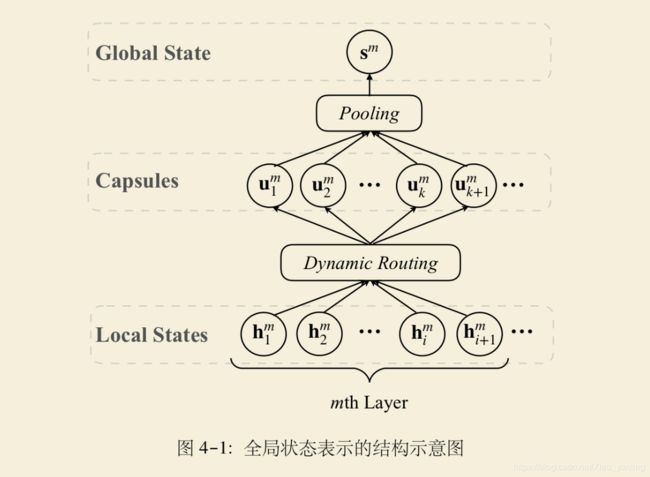
论文中生成全局句子表示的过程与上述胶囊网络过程类似,其中,输入为有 I \mathrm{I} I个词的句子,输出为一个全局句子表示向量,(猜想:论文选用胶囊网络的原因是,最终要获得的结果是向量,胶囊网络在计算过程中都是向量形式,而神经网络计算过程中是标量的形式。)
论文提出了注意力池化方案,能够与将各个胶囊起到的不同作用进行区分。
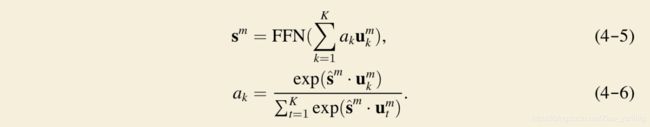
聚合多层表示
不直接使用最后一层局部表示生成的全局状态表示,而是聚集不同层表示的结构,获得更完整的全局状态表示。
(1)前馈聚集结构,采用残差网络。
(2)门循环单元,实现循环聚集。
全局表示学习语义信息
利用词预测机制,通过预测目标端所有需要生成的词来作为语义监督。
全局表示学习句法信息
通过预测目标端句子的线性化句法树序列来约束控制全局状态的生成过程。
利用单语数据增强神经机器翻译
这个部分有待深入阅读
双向记忆交互式神经机器翻译
(1)问题:目前,最先进的Seq2Seq模型仍然无法像人类那样产生令人满意的句子。
单向交互模型:从左到右修改翻译输出。
单向交互模型可能存在的问题:
单向交互模型只能重新生成修改部分,而不是更新整个句子。造成了每次修改都应该修改最左边的错误的约束。
很少能利用修改后的句子。
(2)提出的方法:顺序双向解码器:从句子两端执行交互式NMT,修改句子两端的翻译,允许人们修改翻译的任意单词,在得到修改后更新整个句子。人工首先修改最关键的错误,然后模型更新整个句子,自动修复小错误。
分别使用在线学习(在先前修改的句子上微调Seq2Seq模型,使参数适应特定的话语或领域)和修订记忆方法的句子级别和单词级别的交互历史,避免在交互过程中出现相同的错误。
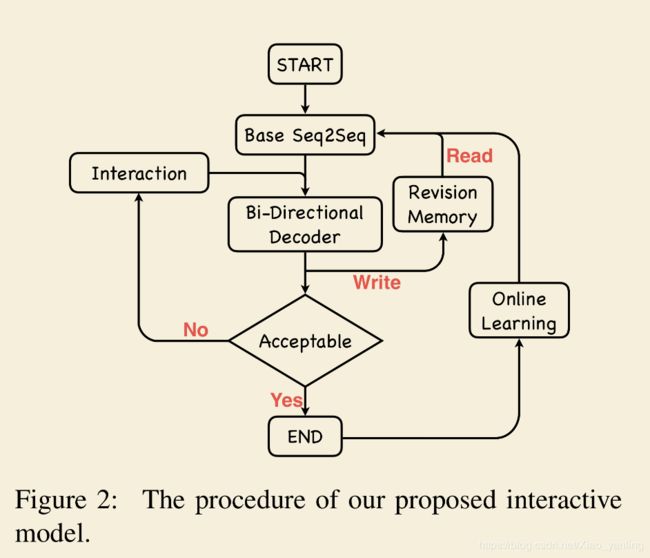
(3)Sequentional Bi-Directional Decoding
两个解码器:前向解码器 f → f^\rightarrow f→和反向解码器 f ← f^\leftarrow f←,它们共享相同的编码器,但顺序工作。
在交互过程中,首先前向解码器作为生成基本翻译 y = y 1 , . . . , y j , . . . y={y_1,...,y_j,...} y=y1,...,yj,...的模型,给定要修改的部分为{ y j → y j r y_j\rightarrow{y_j^r} yj→yjr},然后前向解码器更新翻译中修改的部分(和单向模型一样),那么前向解码器新的解码状态为: s → ′ = f → ( y j r , s j , c j + 1 ′ ) s^{\rightarrow'}=f^\rightarrow(y_j^r,s_j,c^{'}_{j+1}) s→′=f→(yjr,sj,cj+1′)
新得到的翻译的句子为: { . . . y j − 1 , y j r , y j + 1 ′ , y j + 2 ′ , . . . } \{...y_{j-1},y_j^r,y_{j+1}^{'},y_{j+2}^{'},...\} {...yj−1,yjr,yj+1′,yj+2′,...}
y j r y_j^r yjr右边的是新生成的。
将 { . . . y j − 1 , y j r , y j + 1 ′ , y j + 2 ′ , . . . } \{...y_{j-1},y_j^r,y_{j+1}^{'},y_{j+2}^{'},...\} {...yj−1,yjr,yj+1′,yj+2′,...}输入给反向解码器,产生:
s j − 1 ← ′ = f l e f t a r r o w ( y j r , s j ′ , c j − 1 ′ ) s^{\leftarrow'}_{j-1}=f^{leftarrow}(y_{j}^r,s_j^{'},c_{j-1}^{'}) sj−1←′=fleftarrow(yjr,sj′,cj−1′)
由此反向解码器可以生成新的左部。
最终输出:
{ . . . , y j − 2 ′ , y j − 1 ′ , y j r , y j + 1 ′ , y j + 2 ′ , . . . } \{...,y_{j-2}^{'},y_{j-1}^{'},y_j^r,y_{j+1}^{'},y_{j+2}^{'},...\} {...,yj−2′,yj−1′,yjr,yj+1′,yj+2′,...}
(4)针对一轮交互中存在多处修改提出的方法:
采用网格搜索俩存储包含先前修改的部分翻译,在网格搜索之后,所有先前的修改将包含在最终翻译输出中。
(5)句子级别的在线学习
目标函数:
L O = 1 J ′ ∑ j = 1 J ′ l o g P ( y j ′ ∣ y < j ′ , x ) L^O=\frac{1}{J^{'}}\sum^{J^{'}}_{j=1}logP(y_j^{'}|y^{'}_{<j},x) LO=J′1j=1∑J′logP(yj′∣y<j′,x)
x x x:源句
根据此目标函数微调双向模型。