机器学习中的kNN及其Python实例

在2006年12月召开的 IEEE 数据挖掘国际会议上（ICDM， International Conference on Data Mining），与会的各位专家选出了当时的十大“数据挖掘算法”（ top 10 data mining algorithms ）， kNN算法即位列其中。

该算法思路简洁，但是在实践中却相当有效。如果你对其算法原理仍不甚了解，你可以参考本博客之前的文章《机器学习中的kNN算法及Matlab实例》。KNN算法不仅可以用于分类，还可以用于回归，但主要应用于分类。在此前的文章中，我们给出的实例是基于Matlab实现的。本文将演示在Python语言中利用scikit-learn提供的函数来进行基于 kNN的Classification实例。最后，本文还会介绍利用KNN进行回归的基本思路。

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数 据结构、机 器学习、数据挖 掘、统计分析方法、自 然语 言处理。

---------------------------------------------------

一、在Python中读入iris数据集，并进行图形化的展示

这里所使用的数据同样是经典的iris数据集，这一点同文章《机器学习中的kNN算法及Matlab实例》一致。注意原数据集中的每一个数据点都是一个4维向量，我们仅取Petal.Length和Petal.Width这两列数据，一共150行，三类鸢尾花每类各50行。

首先引入各种必要的package。

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sklearn import neighbors
>>> from sklearn import datasets

接下来，载入数据集。

>>> iris = datasets.load_iris()
>>> X = iris.data[:, 2:4] ##表示我们只取特征空间中的后两个维度
>>> y = iris.target

然后我们可以借助下面的代码来用图形化的方式展示一下数据的分布情况：

>>> color = ("red", "blue", "green")  
###分别绘制三组样本的散点图
>>> plt.scatter(X[:50, 0], X[:50, 1], c = color[0], marker='o', label='setosa')
>>> plt.scatter(X[50:100, 0], X[50:100, 1], c = color[1], marker='^', label='versicolor')
>>> plt.scatter(X[100:, 0], X[100:, 1], c = color[2], marker='+', label='Virginica') 

>>> plt.xlabel('petal length')
>>> plt.ylabel('petal width')
>>> plt.legend(loc=2)
>>> plt.show()

执行上述代码，结果如下图所示：

---------------------------------------------------

二、利用scikit-learn进行基于kNN的分类

回想一下，kNN分类器的基本原理。以近邻为基础的分类器是一类特殊的机器学习模型，因为它不像SVM或者感知机那样设法从一个hypothsis set中基于机器学习算法选出一个最佳的hypothsis。我们称这种以近邻为基础的分类器为基于实例的学习（instance-based learning）或者非泛化学习（non-generalizing learning）：它不会尝试构建一个普遍的内部模型（general internal model），而只是把训练数据的实例简单的存储起来。最终的分类任务只是通过对需要分析或预测的点周围（一个邻域内或者固定数量的）最近邻，进行投票而完成的。

scikit-learn中提供了两种不同的NN分类器：KNeighborsClassifier 和RadiusNeighborsClassifier，其中前者会接收用户输入的一个整数k，然后搜索k个最近邻（再进行投票）。后者则会需要一个浮点数r来作为半径，然后让这个半径范围内的点进行投票。下面将主要以 KNeighborsClassifier为例来演示kNN分类的具体实施。

scikit-learn中提供的KNeighborsClassifier的参数有很多，其中比较常用的包括：n_neighbors 用以指定kNN中k的值（缺省值为5），algorithm 参数的可选值有：‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’，这其实主要是指用来寻找最近邻的具体算法，如果设定为‘auto’，系统会根据传给fit方法的参数来选择最合适的算法。weights 参数指定了各个最近邻的权重分布方式，其默认值为‘uniform’，也就表示所有nearest neighbor的权重都一样。另外也可以选择‘distance’，此时就表示权重和距离相关。metric表示距离的度量方式，默认值为‘minkowski’，当p=2时，‘minkowski’距离其实就是欧几里得距离。其他参数的意义请参考文献【1】。

下面来利用KNeighborsClassifier为鸢尾花dataset建立kNN模型。注意，此处的kNN模型并不像SVM那样会从hypothesis set中pick up the best one，它其实只是把训练实例存起来，因此这里所建立的模型其实是把训练实例存进一棵Tree中（例如 k-d-tree），所得之模型也就是这样的一棵Tree。而这样的结构，主要是为了计算NN时更加快捷。

>>> clf = neighbors.KNeighborsClassifier(n_neighbors = 5,
                     algorithm = 'kd_tree', weights='uniform')
>>> clf.fit(X, y)
KNeighborsClassifier(algorithm='kd_tree', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=15, p=2,
           weights='uniform')

然后利用已经建立的模型，预测一下两个新的数据点应该被分到哪一类中。

>>> new_data = [[4.8, 1.6], [2, 0.6]]
>>> result = clf.predict(new_data)
>>> result
array([1, 0])

然后再进行一下图形化的显示。

>>> plt.plot(new_data[0][0], new_data[0][1], c = color[result[0]], marker='x', ms= 8)
>>> plt.plot(new_data[1][0], new_data[1][1], c = color[result[1]], marker='x', ms= 8)
>>> plt.show()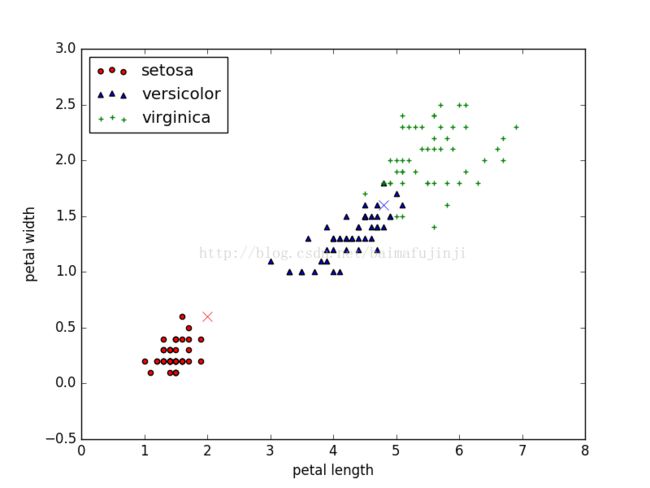

结果如下图所示，可见分类正确，新引入的点其分类以颜色来表示。

---------------------------------------------------

三、基于kNN的回归

kNN不仅可以用于分类，还可以用于回归。为了便于理解，下面将结合一个例子来说明，该例子来自文献【2】。如下表所示，我们的数据集有两个维度：一个是房屋的Age，一个是房屋的Loan，我们的目标是预测在给定上述两个数据时房屋的HPI。假设此处我们使用的距离为欧式距离。

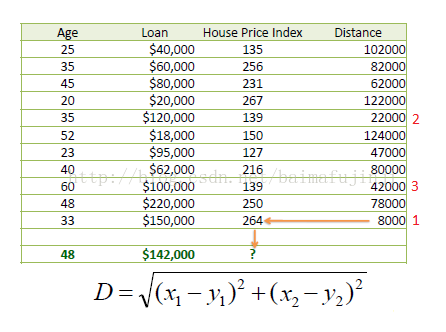
例如，现在有一个数据是Age=48，Loan=142000，当k=1是，我们从已知的数据集中选择一个与这组数据最接近的，此时可以得到回归值为264，即

D = Sqrt[(48-33)^2 + (142000-150000)^2] = 8000.01  >>  HPI = 264

如果k=3，则选取三个最近邻，并取平均，即

HPI = (264+139+139)/3 = 180.7

但是上面这个数据集如果简单使用欧式距离，会存在一个问题，即Loan的数值要远高于Age，所以其权重也会比较大。所以在很多时候，面对这种情况，我们需要对数据进行归一化。例如：

以上便是利用KNN进行回归的基本原理。有兴趣的读者也可以利用scikit-learn 中提供的方法亲身体验一下kNN回归的应用。

参考文献：

【1】http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier

【2】http://www.saedsayad.com/k_nearest_neighbors_reg.htm

（本文完）