Leetcode题解 0012期

（今天刷题群吐槽刷题速度过快，其实个人感觉也有点快了……毕竟手上还有其他任务，今天刷题群停一天，趁机摸一些困难的题目，其余中间空出的难度标注为简单或者中等的题目下一期或者刷到之后再作解释）

0041 缺失的第一个正数【First Missing Positive】

题目：
给定一个未排序的整数数组，找出其中没有出现的最小的正整数。
要求：你的算法的时间复杂度应为 O(n) O ( n ) ，并且只能使用常数级别的空间。

示例：

输入: [1,2,0]
输出: 3

输入: [3,4,-1,1]
输出: 2

输入: [7,8,9,11,12]
输出: 1

题目相对严谨

除Robust以外无需注意太多

解题思路：
又是短题目题，而且要求一开始看到感觉有点变态的，只能有额外的常数空间进行储存，又不让排序，那么只能在原数组上做文章。
思考了一番，发现这题真的非常不错，巧妙的利用数组值本身和数组下标两者区别开来使用，让我想到了当年八皇后从二维数组优化至一维数组的巧妙性。这道题巧妙的利用了正整数的特性，假如说3是没有出现的最小正整数，那么说明1、2一定出现了，那么此时数组长度肯定是大于等于2的，也就是说数组以0、1为下标的数一定存在，按照这样的思路，便可以写出代码，post在这里：

class Solution:
    def firstMissingPositive(self, nums):
        n = len(nums)
        for i in range(0,n):
            if nums[i] < 1 or nums[i] > n:
                nums[i] = n + 1
                #preprocess

        for i in range(0,n):
            val = abs(nums[i])
            if val == n + 1: continue
            if nums[val-1] > 0: nums[val-1] = -nums[val-1] 
            #negative number represents that its (index number + 1) has been found.

        idx = 0
        while idx < n:
            if nums[idx] > 0: break
            idx += 1

        return idx + 1

---

0042题 接雨水【Trapping Rain Water】

题目：
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

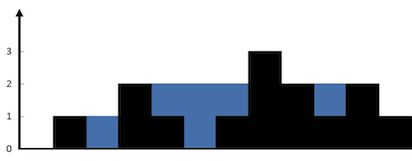
示例：

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

题目相对严谨

需要注意：
1. Robust
2. 边界不算柱子，无法接水，上图中最后一个柱子上不能盛水

解题思路：
这题朴素想法，牛顿出来说一下话，按照重力法则，一条一条看能存多少水，然后如果当下这个地方可以存水，那么把水注入（height[idx] += 1），这样的话，就可以检查每一条是否能存水了，把这个简单的想法实现一下，post代码：

class Solution:
    def check(self, height, k):
        if k == 0 or max(height[0:k]) <= height[k]: return False
        if k == len(height) - 1 or max(height[k:]) <= height[k]: return False
        return True

    def trap(self, height):
        tot = 0
        n = len(height)
        if n == 0 or n == 1: return 0
        h = max(height)

        for i in range(0,h):
            for k in range(0,n):
                if height[k] == i and self.check(height, k):
                    height[k] += 1
                    tot += 1

        return tot

没有做任何优化的情况下，这个代码竟然能过314/315个点，然而最后一个点还是TLE爆掉了，所以这种方法不现实，那么立即想到是否可以提前做预处理，保存当下点位最高的值，然后在进行扫描即可，理解实现代码，如下：

class Solution:
    def trap(self, height):
        n = len(height)
        if n <= 2: return 0
        left = [-1] * n
        right = [-1] * n

        max_idx = 0
        max_height = height[0]
        left[0] = 0
        for i in range(1, n):
            if height[i] >= max_height:
                max_idx = i
                max_height = height[i]
            left[i] = max_idx

        right[n-1] = n - 1
        max_idx = n - 1
        max_height = height[n-1]
        for i in range(n-2, -1, -1):
            if height[i] >= max_height:
                max_idx = i
                max_height = height[i]
            right[i] = max_idx

        tot = 0
        for i in range(0, n):
            tot += min(height[left[i]], height[right[i]]) - height[i]

        return tot

时间复杂度已经降至 O(n) O ( n ) ，而不是原来的 O(n∗h) O ( n ∗ h ) 了，相对最优。

---

0044题 通配符匹配【Wildcard Matching】

题目：
给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 ‘?’ 和 ‘*’ 的通配符匹配。
说明：

• ‘?’ 可以匹配任何单个字符。
• ‘*’ 可以匹配任意字符串（包括空字符串）。

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

两个字符串完全匹配才算匹配成功。

示例：

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

输入:
s = "aa"
p = "*"
输出: true
解释: '*' 可以匹配任意字符串。

输入:
s = "cb"
p = "?a"
输出: false
解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

输入:
s = "adceb"
p = "*a*b"
输出: true
解释: 第一个 '*' 可以匹配空字符串, 第二个 '*' 可以匹配字符串 "dce".

输入:
s = "acdcb"
p = "a*c?b"
输出: false

题目不严谨之处：
1. 中文界面下，最后一个样例的最后“输入”二字应该改为“输出”

除Robust以外无需注意太多

解题思路：
这题完全就是第0010题（https://blog.csdn.net/bright_silmarillion/article/details/80632159）的改编，这次的问号和上次的点号效果相同，而这次的星号比上次的还要复杂，是只要匹配任意字符串即可，0010题的代码以及思路还仍然在脑中回想，那个动归可是很久才想到的，然而这道题提示标签中也有动归和回溯两类，说明上次的思路仍然能用，这里直接套用最优的DP思路，一维数组解决，这里post代码：

class Solution:
    def isMatch(self, s, p):
        s_len = len(s)
        p_len = len(p)
        dp = [False] * (s_len+1)
        dp[0] = True

        for i in range(1, p_len+1):
            if p[i-1] != '*':
                for j in range(s_len, 0, -1):
                    dp[j] = dp[j-1] and (p[i-1]=='?' or s[j-1] == p[i-1])
            else:
                idx = 0
                while idx <= s_len and (not dp[idx]): idx += 1
                while idx <= s_len:
                    dp[idx] = True
                    idx += 1

            dp[0] = dp[0] and p[i-1] == '*'

        return dp[s_len]

写得还是有些区别，emmm，不过一样过了

---

0045题 跳跃游戏 II【Jump Game II】

题目：
给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。

示例：

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

题目相对严谨

除Robust以外无需注意太多

解题思路：
我什么时候做过跳跃游戏1？印象中好像并没有……
非负整数，真的太好了，如果有负数的话这题就绝对不能仅仅是贪心了……标签在贪心下面，那么显而易见的算法，post代码：

class Solution:
    def jump(self, nums):
        n = len(nums)
        if n == 0 or n == 1: return 0
        idx = pos =0
        cnt = 0
        while True:
            new_pos = pos
            while idx <= pos:
                new_pos = max(new_pos, idx + nums[idx])
                idx += 1

            cnt += 1
            pos = new_pos
            if pos >= n-1: break

        return cnt