算法图解part8：贪婪算法

1.贪婪算法介绍

贪婪算法_百度百科：
算法基本思路：从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。

简单直接的描述，就是指每步都选择局部最优解，最终得到的就是全局最优解。
与分而治之（part4）类似，贪婪算法是一种解决问题的方案。

2.背包问题

有些情况下，完美是优秀的敌人。如果你只需要找到一个大致解决问题的算法，贪婪算法挺不错，因为实现容易，结果与正确结果相当接近。但是一般情况下，得不到最优解（只是近似）。

举两个栗子：

你在一家家具公司工作，需要将家具发往全国各地，为此你需要将箱子装上卡车。每个箱子的尺寸各不相同，你需要尽可能利用每辆卡车的空间，为此你将如何选择要装上卡车的箱子呢？请设计一种贪婪算法。使用这种算法能得到最优解吗？

• 选择可以装入卡车中最大的箱子，不断重复，直到不能再装，这种算法得不到最优解。

你要去欧洲旅行，总行程为7天。对于每个旅游胜地，你都给它分配一个价值——表示你有多想去那里看看，并估算出需要多长时间。你如何将这次旅行的价值最大化？请设计一种贪婪算法。使用这种算法能得到最优解吗？

• 断地挑选可以在剩下的时间内完成的价值最大的活动，直到剩下的时间不能够完成任何活动为止。同样这种算法得不到最优解。

3.集合覆盖问题

3.1 广播台覆盖区域问题

假设你办了个广播节目，要让全美个州的听众都收听得到，为此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，因此你试图在尽可能少的广播台播出。现有广播台名单如下：

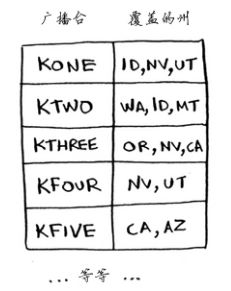
每个广播台都覆盖特定的区域，不同广播台的覆盖区域可能重叠。

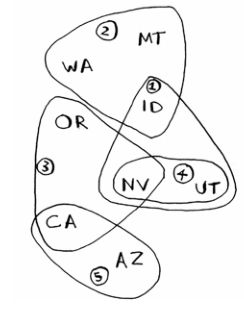
如何找出覆盖全美个州的最小广播台合集呢？ 下面是解决步骤：

• 1.列出每个可能的广播台集合，这被称为幂集（power set）。可能的子集有$2^n$个。
• 2.在这些集合中，选出覆盖全美50个州的最小集合。

那么问题来了，计算每个可能的广播台子集需要很长的时间。

因此，可以尝试使用贪婪算法。

3.2 使用贪婪算法解决

用贪婪算法可得到非常接近的解：

• ①选出这样一个广播台，它覆盖了最多的未覆盖的州。即使有重复的州也没有关系
• ②重复第一步，直到覆盖了所有的州

这是一种近似算法。判断近似算法优劣的标准如下：

• ①速度有多快
• ②得到的近似解与最优解的接近程度。 本博客未解决的问题：如何去判断这个程度？

因此贪婪算法是一个不错的选择，它们不仅简单，而且通常运行速度很快。在这个例子中贪婪算法的运行时间为$O(n^2)$,而所有子集有$2^n$个，运行时间为$O(2^n)$。（其中n为广播台数量）

python代码实现：

第一步：准备工作
首先，创建一个列表，其中包含要覆盖的州

states_needed=set(["mt","wa","or","id","nv","ut","ca","az"])

可供选择的广播清单，用散列表来表示它：

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

用一个集合来保存最终选择的电台

final_stations = set()

第二步：计算答案
需要遍历所有的广播台，从中选择覆盖了最多的未覆盖州的广播台。将整个广播台存储在best_station 中。 states_covered是个集合，包含该广播台覆盖的所有未覆盖的州。for循环迭代每个广播台，并确定它是否是最佳的广播台。
就像是遍历寻找一个集合中元素最多的那个键，键是best_station，对应的元素（与未覆盖的states_needed的交集）是states_covered；
而station, states_for_station分别是当前迭代索引对应的 键与值，covered是交集（该广播台覆盖的所有未覆盖的州）。

while states_needed:#循环直至所需要覆盖的州为空

    best_station = set()#覆盖最多州的广播台
    states_covered = set()#该广播台覆盖的所有未覆盖的州
    
    for station, states_for_station in stations.items():#循环所有（键值）广播站station以及 站对应的覆盖州states_for_station
        covered = states_needed & states_for_station# &取交集
        
        if len(covered) > len(states_covered): 
            best_station = station
            states_covered  = covered
            
    states_needed -= states_covered
    final_stations.add(best_station)

print(final_stations)

python代码如下：

# 创建一个列表，其中包含要覆盖的州
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) # 传入一个数组，被转换为集合

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set() # 使用一个集合来存储最终选择的广播台

while states_needed:

	  best_station = set() # 将覆盖了最多的未覆盖州的广播台存储进去
	  states_covered = set() # 一个集合，包含该广播台覆盖的所有未覆盖的州
  
	  for station, states in stations.items(): # 循环迭代每个广播台并确定它是否是最佳的广播台
		    covered = states_needed & states # 计算交集
	    
		    if len(covered) > len(states_covered): # 检查该广播台的州是否比best_station多
			      best_station = station # 如果多，就将best_station设置为当前广播台
			      states_covered = covered

	  states_needed -= states_covered # 更新states_needed
	  final_stations.add(best_station) # 在for循环结束后将best_station添加到最终的广播台列表中

print(final_stations) # 打印final_stations

运行结果

{‘kfive’, ‘ktwo’, ‘kthree’, ‘kone’}

拓展：set()方法 与 差并交 集

• python集合set()方法：集合中不能出现重复的元素。（该广播栗子中，多个广播台可能会有相同的覆盖地区，使用该方法可以使元素不会重复）

arr = [1,1,2,3,4,4]
set(arr)

运行结果：

{1, 2, 3, 4}

• 在上述算法中，有一段代码很有趣

covered = states_needed & states # 计算交集

它 & 是用来进行集合之间的相关计算，在此介绍下并集、交集和差集

• ①并集意味着将集合合并；
• ②交集意味着找出两个集合中都有的元素；
• ③差集意味着将从一个集合中剔除出现在另一个集合中的元素。

举个栗子：

fruits = set(["avocado","tomato","banana"])
vegetables = set(["beets","carrots","tomato"])

fruits | vegetables # 计算并集
>>>{'carrots', 'tomato', 'avocado', 'beets', 'banana'}

fruits & vegetables # 计算交集
>>>{'tomato'}

fruits - vegetables # 计算差集
>>>{'avocado', 'banana'}

vegetables - fruits
>>>{'carrots', 'beets'}

4.NP完全问题

wiki百科：
非决定性多项式集合（英语：non-deterministic polynomial，缩写：NP）是计算理论中最重要的集合之一。它包含P和NP-complete。 P集合的问题即在多项式时间内可以找出解的决策性问题(decision problem)集合。注意NP包含P和NP-complete问题, 因此NP集合中有简单的问题和不容易快速得到解的难题。[NP等不等于P?]是一个计算机界一个知名的大难题。

详细NP问题介绍请参考博客：https://blog.csdn.net/csshuke/article/details/74909562

举个栗子：

• 旅行商问题
  旅行商需要前往不同的城市，需要找到前往所有城市的最短路径。可能的路径如下：

2个城市时，2条；
3个城市时，6条；
4个城市时，24条；
同理：N个城市就是N！条，这被称为阶乘函数。

你需要计算所有的解，并从中选出最小/最短的那个。此博文提到的旅行商问题和集合覆盖问题都属于NP完全问题。

如何识别NP完全问题：

• ①元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
• ②涉及“所有组合”的问题通常是NP完全问题。
• ③不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
• ④如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
• ⑤如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
• ⑥如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

5.总结

• 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
• 贪婪算法易于实现、运行速度快，是不错的近似算法。
• 广度优先搜索、迪杰斯特拉算法是贪婪算法。
• 对于NP完全问题，还没有找到快速解决的方案。
• 面临NP问题时，最佳的做法是使用近似算法。

6.参考资料

《算法图解》第八章：详细的程序思路介绍

P = NP ? 问题的介绍：https://blog.csdn.net/catkin_ws/article/details/92801043
wiki NP介绍：https://zh.wikipedia.org/wiki/NP_(複雜度)
此部分学习算法内容已上传github：https://github.com/ShuaiWang-Code/Algorithm/tree/master/Chapter8