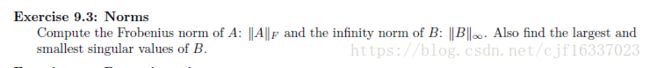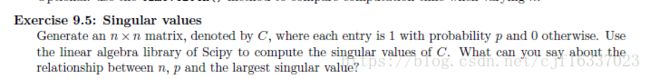第十一周作业 Numpy习题
查阅numpy函数使用的博客:
Numpy线性代数:https://blog.csdn.net/pianoorrock/article/details/79223080
numpy基本方法总结:https://blog.csdn.net/blog_empire/article/details/39298557
生成矩阵A和B,A由随机高斯项组成,B为toeplitz矩阵
n,m值调整至10,15,便于测试
import numpy as np
import numpy.matlib
import scipy
import time
import math
from scipy.linalg import toeplitz
n = 10
m = 15
temp = np.matlib.rand(1,m)
A = np.matlib.randn(n, m) #生成A
B = toeplitz(temp) #生成B
print("Matrix A:")
print(A)
print("Matrix B:")
print(B)
print("\n")Exercise_9_1
常规的矩阵运算
def Exercise_9_1(k):
print("Exercise[9.1]:")
print("A+A:") #A+A
print(A+A)
print("AA^T:") #AA^T
print(A*A.T)
print("A^T*A:") #A^T*A
print(A.T*A)
print("AB:") #AB
print(A*B)
print("A(B-kI) for k = " + str(k))
print(A * (B - k * np.matlib.identity(m)))
print("\n")
Exercise_9_1(1)Exercise_9_2
线性方程求解,用numpy.linalg.solve求解方程
def Exercise_9_2():
print("Exercise[9.2]:")
b = np.matlib.rand(m, 1) #随机生成向量b
print("vector b:")
print(b)
x = np.linalg.solve(B, b)#用numpy.linalg.solve求解方程
print("The x of B*x = b is :")
print(x)
print("\n")
Exercise_9_2()
Exercise_9_3
求A,B的范数 和 B的奇异值的max和min
def Exercise_9_3(F):
print("Exercise_9_3")
print("||A||"+str(F)+" :")
print(np.linalg.norm(A, F)) #用numpy.linalg.norm求范数,求A的F范数
print("||B||∞ : ")
print(np.linalg.norm(B, np.inf))#numpy的inf表示无穷,即求无穷范数
print("singular value of B is :")
u,s,v= np.linalg.svd(B,full_matrices=True) #求奇异值,由svd函数进行svd分解可得
print("max:")
print(max(s))
print("min:")
print(min(s))
Exercise_9_3(2)Exercise_9_4
用高斯项生成矩阵Z,n×n,用幂迭代法求Z的最大特征值和相应的特征向量,直到收敛为止需要多少次迭代?
def Exercise_9_4(n):
start = time.clock()
Z = np.matlib.randn(n, n)
u = np.matlib.rand(n, 1)
print("Matrix Z:")
print(Z)
t1 = 0
t2 = 1
count = 0
while math.fabs(t1 - t2) > 1e-10:
count = count + 1
v = Z * u
t1 = t2
t2 = max(np.abs(v))
u = v / t2
end = time.clock();
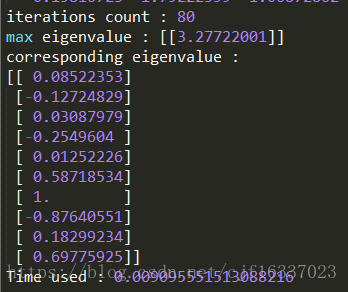
print("iterations count : " + str(count))
print("max eigenvalue : "+ str(t2))
print("corresponding eigenvalue : ")
print(u)
print("Time used : " + str(end - start))
Exercise_9_4(10)此处测试n=10时,迭代次数为80(随机性很强,n=10时迭代次数也不定。。。。)
Exercise_9_5
numpy.random里的二项分布生成C矩阵
#求奇异值,由svd函数进行svd分解可得
def Exercise_9_5(n,p):
print("n : " + str(n) + " p : " + str(p))
C = np.random.binomial(1,p,(n,n))
print("Matrix C:")
print(C)
u, s, v = np.linalg.svd(C)
print("max singular value of C is :")
print(max(s) )
Exercise_9_5()p越接近0.5,其奇异值越大。
Exercise_9_6
def Exercise_9_6(A, z):
print("Matrix A :")
print(A)
print("z : " + str(z))
print(A[0, np.argmin(np.abs(A-z))])
print()
Exercise_9_6(A, z)