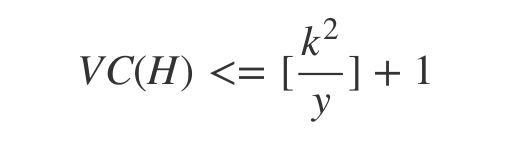【学习笔记】斯坦福大学公开课： cs229 Learning Theory【下】

上回讲到了，当假设空间H是有限集时，当我们的训练数据的数目满足一定要求的时候，使用ERM选出的假设h^的经验误差能够对其泛化误差做一个很好的估计，二者以很大概率非常接近，术语叫做“一致收敛”；而且，h^的泛化误差与理想状况下的假设h*的泛化误差也以大概率接近，我们也得到了对应的一致收敛定理。那么，当H是无限集的时候会怎么样呢？

个人认为，Ng老师这节课讲的不是很透彻，至少我听完一遍之后还是云里雾里的，于是上网搜了牛人的博客看了一下，恍然大悟。这位高人的博客链接我贴在这，感兴趣可以看一看，写得非常清楚，他是听的台大《机器学习基石》。下面我把他的笔记内容争取用概括性的语言复述一遍。now，begin。

首先让我们重新看一看Hoeffding不等式。这个不等式讲了什么呢？说的是对于一堆独立同分布的伯努利随机变量，共n个。这n个样本的平均值可以对此伯努利分布的数学期望做一个很好的估计，如果n很大的话。

而且n越大，这种估计越好，因为此不等式的上界将趋于0.也就是样本期望越来越趋近于总体期望。上次我们说到，正是由这个不等式，我们推出了经验误差和泛化误差在n足够大时一致收敛的道理，我们有

这一步用到了概率论的一个公理。为什么要重新提到hoeffding不等式呢？因为接下来要借助它引出许多新的概念。比如：什么情况下学习是可行的？

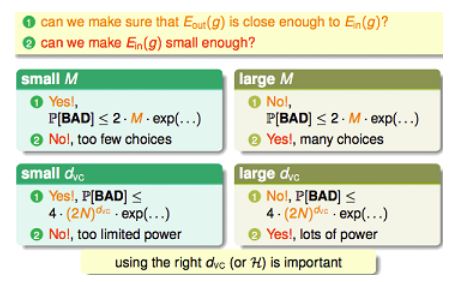
这就要满足两个条件，①我们希望能让模型的经验误差收敛到泛化误差。②我们希望模型能够使经验误差接近于0. 这里，就涉及到了对M的权衡。对于large M，也就是假设空间里面可能包含有更复杂的模型，那我们很容易做到②，因为有许多选择，这么多假设，总有一款适合你（总可以找到使经验误差足够小的），但对于①，就难以满足了，从数学意义上，我们可以看到不等式的上界变大，这说明使得经验误差收敛于泛化误差变得更困难；直观来理解的话，那就是容易过拟合了，因为你可能选择了一个非常复杂的模型。同理，对于small M，也可以用相似的方式来理解，不再赘述。对应的后果是可能欠拟合。

上面的事情算是给了我们一个警告：学习一个问题能不能 成功，不能只看你有多少个训练样本，对于一个欠拟合的模型，你样本再多（N大），经验误差和泛化误差的确收敛到一起了，可是由于你的模型太简单（M小），经验误差根本不趋于0啊！泛化误差自然也不趋于0.Well，that‘s too bad! 也就是说，学习可行与否，受到M和N的同时约束。

我们继续。既然M也很重要，那么我们就来关注关注它。M无限时怎么办？上面的不等式不成立了吗？两种误差收敛不到一起了？

直观上，我们希望用一个有限值来代替无限的M.为什么这么想？注意到我们对推导上面不等式的时候，其实是假设了H中各个h相互独立了的，而实际上，它们之间并非完全独立，而是会有很大重叠（这点也很好理解，大家都长在一起，怎么能一点也不像呢），也就是说，完全有可能“h1：bad→ h2：bad”，这两个事件有可能相关。那么，这也就是说，我们不必被M变成无限大唬住，那一堆概率之和完全有可能小于等于的是一个有限的东西，你直接写成M，未免夸张了。所以，我们想要用一个有限值来代替里面的M，换句话说，H里面就算有 无穷多的假设，也未必都是有效的。

有效的？这又是啥？

增长函数、对分、打散、breakpoint这些概念就要出场了。我们注意到，对于有N个样本的训练集，共有2^N种分类可能（二元分类）；而H所能实现的所有可能的分类情况数目，叫做它能实现的“对分”数；对于变化的N，对分数是变化的，我们叫做H的“增长函数”g。若H中至少存在一个假设，能够实现N的所有可能分类情况，那么称H能够打散这N个样本。显然，在H能打散N的时候，g=2^N。当N增大到某一值k，g不再指数增长了，g<2^k，这个k就叫做breakpoint。而增长函数的值，其实就代表了H中有效假设的数量。

比如，N=3时，无论怎么标记这三个点，都有一种直线能够将他们分开；而对于N =4，有两种情况是直线无论如何也分不开的，这时g=14<2^N=16.

这至少告诉我们，H没有想象中那么强大，它所能表示的分类数是有限的（g有界）。而且，可以证明，增长函数，被最高幂次为k-1次的多项式给限制住

上面这个是VC bound，可以理解为将无限的M用有限的mH(2N)代替处理之后的结果。这时，我想可以把VC维的概念抛出来了。其实，VC维就是k-1，也就是H所能打散的最大点集的大小。VC维的物理意义就是用来表示H的表示能力，也即其中的假设的复杂程度。VC维也大，这种能力越强。

可以证明，H的增长函数，即假设空间中有效的假设函数的数量，是被最高幂次为VC维（break point -1 ）的多项式给限制住的。因此，VC维若存在，那么增长函数就有限，那么由于指数式下降的比多项式增长的更快（见上图），当样本数量达到一定数目时，经验误差和泛化误差就会一致收敛。若VC维无穷大，就证明H的表示能力（power）非常强，能够实现的对分数量无穷多（设想如不是无穷多那么随着样本数N不断增大，总有一个时候H中的所有假设都实现不了shatter，与VC维无穷大矛盾），那么mH(2N)也变成无限值了，从而VCbound就不存在了，两个误差就没法一致收敛。

也可以从VC维的角度来解释过拟合和欠拟合，也就从另一角度解释了什么时候学习是可行的。

有一个实践规律，VC维总是约等于模型的参数数量。而用来训练一个模型的样本数至少应当与模型参数成线性关系，在同一个数量级上。因此可以推出训练模型所需的样本数至少和假设空间的VC维要在同一数量级。而对于SVM，虽然它把样本映射到了一个高维空间，但是它的VC维却不是无穷大的。这是因为最大间隔分类器有一个特点，它的VC维与模型参数无关。一般来说，对于最大间隔为y的SVM，如果样本点均落在半径为R的空间内，VC维服从以下公式：

也就是说，SVM会自动选择一个具有较小VC维的假设，降低模型的复杂度，使得数据更充分。这在样本个数较少时是很有用的，因为模型越复杂，就需要越多的样本数使得经验误差收敛到泛化误差。

Ng的课上还讲到，SVM，逻辑回归，其实都是对ERM的一种凸近似。他们都采用了极大似然估计，其本质跟ERM是一样的。

总结一下，经过这堂课的学习，我对学习理论得到了这样的理解：

若要使一个问题可学习，必须同时满足两个核心条件。ERM是一种基于极大似然估计思想的最朴素的算法，其本质在于M（模型数量）和N（样本数量）的权衡，随着M和N的变化，ERM的学习效果会受到不同的影响，因此，ERM是不完善的，即我们不能只看经验风险，这就启发我们用正则化的方法对模型进行修正（惩罚）来使学习的效果更好。

OK，说了这么多，终于把学习理论这一节写完了，下面会带来Part VI：模型选择和正则化

*****************************************************

参考文献的链接：

http://www.flickering.cn/machine_learning/2015/04/vc%E7%BB%B4%E7%9A%84%E6%9D%A5%E9%BE%99%E5%8E%BB%E8%84%89/点击打开链接