搞懂箱形图(上篇)
箱形图,也叫盒须图,盒式图,boxplot。有95%的把握猜中你现在已经不太确定,这图中有几条线?每条线代表什么意思?中间的那条线代表的究竟是算数平均数还是中位数,还是众数?
再问的深点,箱形图存在的意义为何?之于数据分析的实践意义在哪里?
接下来,带你从概念开始,一步步剖析箱形图以及背后的故事。
1. 感性认识箱形图
箱形图是John Wilder Tukey的一项重大发明。Tukey先生1915年出生于美国麻省的新贝德福德。他22岁的时候在布朗大学获得了硕士学位,之后又在普林斯顿大学拿到了化学博士。有趣的是,他并没有直接开始让他青史留名的统计学工作,而是在二战期间进入了火控研究室,在那里,大量武器相关的研究最终都转而需要先解决统计学问题。从此,Tukey改变了自己的人生方向,一代统计学大师即将出现。
箱形图最大的优点就是不受异常值的影响,可以以一种相对稳定的方式描述数据的离散分布情况。默念两遍,箱形图不受异常值的影响,这很重要。
为了更形象的说明,我们先画个图,看图说话。以下Python代码在Anaconda的Jupyter中实现:
%matplotlib inline
import matplotlib
from matplotlib import pyplot as plt
matplotlib.use('qt4agg')
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.family']='sans-serif'
sample =[1,6,2,7,4,2,3,3,8,25,30]
plt.boxplot(sample)
plt.title('箱型图')
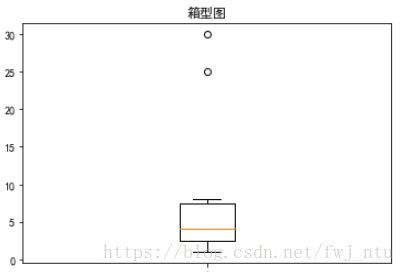
首先从外观上感知这是个什么东东。中间是个矩形块,可以把它想象成一个盒子。盒子里面有一条线,外面有两个形似T的东西。哦,最外面还有两个空心的圆圈,这个可不是所有的箱形图都会有。接下来一一解释这些玩意儿。
2. 箱形图五要素
有一件重要的点,要交代一下,不然可能要被大多数人给忽略掉了。画箱型图,需要计算分位数,若你拿到的这组数据不是顺序排列的,首先要对数据进行排序。
2.1 中位数
中位数,即二分之一分位数。将数据从小到大进行排序,若数据的个数n是基数,则中位数所在的位置即为(n+1)/2的位置。若数据的个数n是偶数,则中位数为第n/2、第n/2+1两个数的算数平均值。
import numpy as np
sample =[1,6,2,7,4,2,3,3,8,25,30]
np.percentile(sample,50)
这组数据的中位数就是4.0。
2.2 下四分位数Q1
四分之一分位数位于箱型图的下方,所以也叫“下四分位数”。
强调一下,四分位数的求法,是将序列平均分成四份。具体的计算目前有(n+1)/4与(n-1)/4两种,一般使用(n+1)/4,即四分之一分位数即第(n+1)/4个数,当然这个结果可能是个分数。结果是分数时,具体的计算后文再讲。
2.3 上四分位数Q3
四分之三分位数位于箱型图的上方,所以也叫“上四分位数”。
强调一下,四分位数的求法,是将序列平均分成四份。具体的计算目前有(n+1)/43与(n-1)/43两种,一般使用(n+1)/43,即四分之三分位数即第(n+1)/43个数。
2.4 内限
目前我们文章中看到的这两个T形的盒须就是内限。上面的T形线段所延伸到的极远处,是Q3+1.5IQR(其中,IQR=Q3-Q1)与剔除异常值后的极大值两者取最小,下面的T形线段所延伸到的极远处,是Q1-1.5IQR与剔除异常值后的极小值两者取最大。
3. 箱形图与异常址清洗
在上面的箱型图中,看到了两个圆圈,这两个圆圈就代表2个异常值。
箱形图最重要的用途就是识别异常值。数据清洗中,作用很大哦。今天先到这里~
