Torch深度学习的60分钟教程(翻译)
这篇博客是官方Tutorial的翻译(加一丢丢自己的见解吧),原文链接为https://github.com/soumith/cvpr2015/blob/master/Deep%20Learning%20with%20Torch.ipynb
什么是Torch?
Torch是一个基于Lua [JIT]的科学计算框架,具有强大的CPU和CUDA后端。
Torch的优点:
•高效的Tensor库(如NumPy),具有高效的CUDA后端
•神经网络包 - 构建具有自动区分的任意非循环计算图
•还有快速的CUDA和CPU后端
•良好的社区和行业支持 - 数百个社区建立和维护的包。
•易于使用多GPU支持和并行化神经网络
开始之前再说一句
•基于Lua并运行Lua-JIT(即时编译器),速度很快
•Lua非常接近javascript。
•默认情况下,变量是全局变量,除非使用local关键字。全局变量不需要声明,给一个变量赋值后即创建了这个全局变量,访问一个没有初始化的全局变量也不会出错,只不过得到的结果是:nil。
•只有一个内置的数据结构,表,用{}表示。表为哈希表和数组。
•索引从1开始。(啊,好清新脱俗的设定啊)
•foo:bar()与foo.bar(foo)相同
顺便讲下lua的一丢丢语法吧~
-- 单行注释
--[[
多行注释
多行注释
--]]
.. 连接两个字符串 如a..b ,其中 a 为 "Hello " , b 为 "World", 输出结果为 "Hello World"。
# 一元运算符,返回字符串或表的长度。 #"Hello" 返回 5开始
在Torch中,x=torch.funcname(...)与x:funcname(...)是等价的。字符串,数字,表格
a = 'hello'
print(a)
b = {}
b[1] = a
print(b)
b[2] = 30
for i=1,#b do -- Lua中#操作符表示表的长度
print(b[i])
endTensor乘法
a = torch.Tensor(5,3) -- 构建一个未初始化的5x3矩阵
a = torch.rand(5,3)
print(a)
b=torch.rand(3,4)
-- 矩阵 - 矩阵乘法:语法1
a*b
-- 矩阵 - 矩阵乘法:语法2
torch.mm(a,b)
-- 矩阵 - 矩阵乘法:语法3
c=torch.Tensor(5,4)
c:mm(a,b) -- 将结果存储在c中CUDA Tensors
可以使用:cuda函数将tensor移动到GPU上
require 'cutorch';
a = a:cuda()
b = b:cuda()
c = c:cuda()
c:mm(a,b) -- done on GPUTensor加法:元素的数量必须匹配,但维度和样式可以不相同。
x = torch.Tensor(2, 2):fill(2) -- 用2填充2*2的矩阵
y = torch.Tensor(4):fill(3)
-- 矩阵加法语法1:将tensor1添加到tensor2并将结果放入res。 元素的数量必须匹配,但维度和样式可以不同
-- torch.add([res], tensor1, tensor2)
x:add(y) -- 将y加到x中,结果存储在x中
-- 矩阵加法语法2:将tensor2的元素乘以标量值并将其添加到tensor1。 元素的数量必须匹配,但维度和样式可以不同
-- torch.add([res,] tensor1, value, tensor2)
x:add(2, y)
输出:
> x
5 5
5 5
[torch.DoubleTensor of size 2x2]
> x
8 8
8 8
[torch.DoubleTensor of size 2x2]神经网络
Torch中的神经网络可以使用nn包构建。
require 'nn';模块用于构建神经网络。 每个模块都是神经网络,但可以与其他网络使用容器(containers)组合来创建复杂的神经网络。
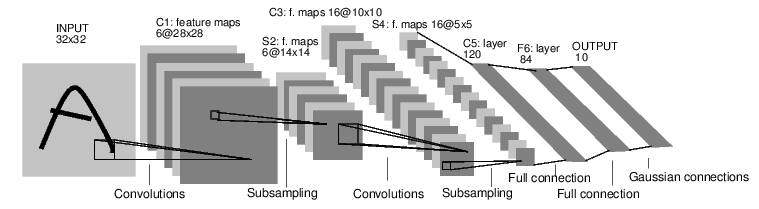
例如,看看这个分类数字图像的网络:
它是一个简单的前馈网络。
它接受输入,一个接一个地通过几个层输入,然后最终给出输出。
这样的网络容器是nn.Sequential,输入通过几层模块产生输出。
net = nn.Sequential()
net:add(nn.SpatialConvolution(1, 6, 5, 5)) -- 1个输入图像通道,6个输出通道,5x5卷积内核
net:add(nn.ReLU()) -- 添加非线性激励函数
net:add(nn.SpatialMaxPooling(2,2,2,2)) -- max-pooling操作,寻找2x2窗口中的最大值
net:add(nn.SpatialConvolution(6, 16, 5, 5))
net:add(nn.ReLU())
net:add(nn.SpatialMaxPooling(2,2,2,2))
net:add(nn.View(16*5*5)) -- 从16x5x5的3维矩阵重塑为16*5*5的1维矩阵
net:add(nn.Linear(16*5*5, 120)) -- 完全连接层(输入和权重之间的矩阵乘法)
net:add(nn.ReLU())
net:add(nn.Linear(120, 84))
net:add(nn.ReLU())
net:add(nn.Linear(84, 10)) -- 在这个例子中,网络的输出数量是10
net:add(nn.LogSoftMax()) -- 将输出转换为对数概率,以助于分类
print('Lenet5\n' .. net:__tostring());nn容器的其他示例如下图所示:
torch中的每个神经网络模块都具有一个前向和后向函数。forward(输入)函数,用于计算给定输入的输出,使输入通过网络流动。 backward(输入,梯度)函数,它将根据传入的梯度区分网络中的每个神经元。这是通过链规则完成的。
input = torch.rand(1,32,32) -- 传递随机矩阵作为网络的输入
output = net:forward(input)
print(output)
net:zeroGradParameters() -- 使网络的内部梯度缓冲区归零(稍后会介绍)
gradInput = net:backward(input, torch.rand(10))
print(#gradInput)损失函数
当你在训练让一个模型时,你会通过反馈知道它做得如何。客观度量模型性能的函数称为损失函数。
典型的损失函数接受模型的输出和分类准确性,并计算一个量化模型性能的值。
然后,该模型纠正自己以使得损失变小。
在torch中,损失函数就像神经网络模块一样实现,它们有两个功能 - 前向(输入,目标),后向(输入,目标)
例如:
criterion = nn.ClassNLLCriterion() -- 多分类的负对数似然准则
criterion:forward(output, 3) -- 实际分类的编号:3
gradients = criterion:backward(output, 3)
gradInput = net:backward(input, gradients)回顾一下目前说过的内容
•网络可以有多层
•网络在正向传播中接收输入并产生输出
•损失函数,也即torch的评价模块(criterion)计算网络的损失及与输出有关的梯度。
•网络在其反向传递中采用(输入,梯度)对,并计算关于网络中每个层(和神经元)的梯度。
细节补充——神经网络层可以具有可学习的参数。
卷积层通过学习来适应输入数据和要解决的问题。
最大池层没有可学习的参数。 它只是寻找本地窗口中的最大值。
torch中具有可学习的权重通常包含.weight(以及可选的.bias)
m = nn.SpatialConvolution(1,3,2,2) -- 3个2x2内核
print(m.weight) -- 权重是随机初始化的
print(m.bias) -- 卷积层中的操作是:输出=卷积层(输入,权重)+偏差学习层中还有另外两个重要字段, gradWeight和gradBias。 gradWeight积累每个权重的梯度,gradBias记录每个偏差。
培训网络
为了让网络自行调整,随机梯度下降通常会执行以下操作:
weight = weight + learningRate * gradWeight [等式1]
随着时间的推移,这种更新将调整网络权重,使损失函数变少。
好的,现在是时候讨论一个问题:是谁访问神经网络中的每一层并根据公式1更新权重?
这个问题有多个答案,但我们将使用最简单的答案。
我们将使用神经网络模块附带的简单SGD训练器:nn.StochasticGradient。
它有一个功能:在给定数据集数据集上进行训练网络,并显示数据集的不同样本是如何影响网络的变化。
关于数据
通常,当您必须处理图像,文本,音频或视频数据时,您可以通过使用标准函数(如image.load或audio.load)方便地将数据加载到torch.Tensor或Lua表中。
现在让我们使用一些简单的数据来训练我们的网络。
我们将使用CIFAR-10数据集,它的标签种类有以下几种:'飞机','汽车','鸟','猫','鹿','狗','青蛙','马','船', '卡车'。
CIFAR-10中的图像尺寸为3×32×32,即尺寸为32×32像素的3通道彩色图像。
该数据集共有50,000个训练图像和10,000个测试图像。
我们现在需要5个步骤来训练我们第一个torch神经网络
1、加载和规范化数据
2、定义神经网络
3、定义损失函数
4、训练网络
5、测试网络
1、加载和标准化数据
今天,为了节省时间,我们事先准备好数据到4D torch ByteTensor,大小为50000x3x32x32(训练数据)和10000x3x32x32(测试数据)。让我们加载数据并进行检查。(不知道是官方数据写错了还是咋的,我两个数据集大小都是10000)
require 'paths'
if (not paths.filep("cifar10torchsmall.zip")) then
os.execute('wget -c https://s3.amazonaws.com/torch7/data/cifar10torchsmall.zip')
os.execute('unzip cifar10torchsmall.zip')
end
trainset = torch.load('cifar10-train.t7')
testset = torch.load('cifar10-test.t7')
classes = {'airplane', 'automobile', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck'}
print(trainset)
print(#trainset.data)让我们显示一个图像:
itorch.image(trainset.data[100]) -- 显示数据集中的第100个图像
print(classes[trainset.label[100]])在这里本人踩了一大个坑(悲惨过程),原本我是在sublime上运行的,跑的这步的时候说没有itorch,按官网装了itorch又说没image。最后搜了以下有大大说这个得在notebook上运行,在jupyter上配lua的环境即可(配置教程)。
要在nn.StochasticGradient中使用数据集,必须根据其文档对数据集进行一番处理。
1、数据集必须具有:函数size()
2、数据集必须具有[i]索引,以便通过dataset[i]来操作datset中的第i个样本。
两者都可以快速完成:
-- 可以暂且忽略setmetatable,它是超出本教程范围的功能。 setmetatable的功能是设置索引运算符。
setmetatable(trainset,
{__index = function(t, i)
return {t.data[i], t.label[i]}
end}
);
trainset.data = trainset.data:double() -- 将数据从ByteTensor转换为DoubleTensor。
function trainset:size()
return self.data:size(1)
end
print(trainset:size()) -- 小小测试一下
print(trainset[33]) -- 加载样本号33
itorch.image(trainset[33][1])在处理数据(通常在数据科学或机器学习)中,我们可以做的最重要的事情之一是使数据的平均值为0.0,标准偏差为1.0。
在我们数据处理的最后一步也来这么做吧。
为此,我们通过下面例子进行向您具体介绍tensor索引运算符:
redChannel = trainset.data[{ {}, {1}, {}, {} }] -- 因为traindata.set是四维大小分别是{10000,3,32,32}的tensor
-- 因此该索引对应的内容是{所有图像,第一个通道,所有垂直像素,所有水平像素}
print(#redChannel)在索引运算符中,以[{}]开头可以对tensor各维的元素进行分开操作。 您可以使用{}选择维度中的所有元素,或使用{i}选择特定元素,其中i是元素索引。 还可以使用{i1,i2}选择一区间的元素,例如{3,5}选择第3,4,5个元素。
练习:选择第150~300的数据
sel = trainset.data[{ {150,300}, {}, {}, {} }]
-- 输出图像
for i=1,151,1 do
itorch.image(sel[i])
end回到标准化处理,使用我们在上面学到的索引操作符来完成此操作很简单。
mean = {} -- 存储均值,以便将来测试集标准化
stdv = {} -- 存储偏差
for i=1,3 do -- 在每个图像颜色通道上
mean[i] = trainset.data[{ {}, {i}, {}, {} }]:mean() -- 均值
print('Channel ' .. i .. ', Mean: ' .. mean[i])
trainset.data[{ {}, {i}, {}, {} }]:add(-mean[i]) -- 减去均值
stdv[i] = trainset.data[{ {}, {i}, {}, {} }]:std() -- 标准差
print('Channel ' .. i .. ', Standard Deviation: ' .. stdv[i])
trainset.data[{ {}, {i}, {}, {} }]:div(stdv[i]) -- 除以标准差
end现在训练数据已归一化并可随时使用。
2.定义神经网络
修改上文的神经网络使它可以接收3通道图像(而不是定义的1通道图像)。
net = nn.Sequential()
net:add(nn.SpatialConvolution(3, 6, 5, 5)) -- 3个图像输入通道,6个输出通道, 5x5卷积核
net:add(nn.ReLU()) -- 添加非线性激励函数
net:add(nn.SpatialMaxPooling(2,2,2,2)) -- max-pooling操作,寻找2x2窗口中的最大值
net:add(nn.SpatialConvolution(6, 16, 5, 5))
net:add(nn.ReLU())
net:add(nn.SpatialMaxPooling(2,2,2,2))
net:add(nn.View(16*5*5)) -- 从16x5x5的3维矩阵重塑为16*5*5的1维矩阵
net:add(nn.Linear(16*5*5, 120)) -- 完全连接层(输入和权重之间的矩阵乘法)
net:add(nn.ReLU())
net:add(nn.Linear(120, 84))
net:add(nn.ReLU())
net:add(nn.Linear(84, 10)) -- 在这个例子中,网络的输出数量是10
net:add(nn.LogSoftMax()) -- 将输出转换为对数概率,以助于分类3.定义损失函数
让我们使用对数似然分类损失函数,这适合大多数分类问题。
criterion = nn.ClassNLLCriterion()4.训练神经网络
事情现在开始变得有趣了。
我们首先定义一个nn.StochasticGradient对象。 然后我们将数据集提供给这个对象的函数:train(),这将使训练自动开始。
trainer = nn.StochasticGradient(net, criterion)
trainer.learningRate = 0.001
trainer.maxIteration = 5 -- 只做5轮训练
trainer:train(trainset)5.测试网络,输出准确性
我们已经在训练数据集上训练了5轮,但我们需要检查网络是否已经学到了什么。我们将通过神经网络分类的情况与实际标签进行检查。 如果预测正确,我们将样本添加到正确预测列表中。
好的,第一步, 让我们从测试集中显示一个图像开始。
print(classes[testset.label[100]])
itorch.image(testset.data[100])现在让我们使用训练数据的均值和标准偏差来规范化测试数据。
testset.data = testset.data:double() -- 将数据从ByteTensor转换为DoubleTensor。
for i=1,3 do -- over each image channel
testset.data[{ {}, {i}, {}, {} }]:add(-mean[i]) -- 减去均值
testset.data[{ {}, {i}, {}, {} }]:div(stdv[i]) -- 除以标准差
end
-- 输出第100个样本的均值和标准差
horse = testset.data[100]
print(horse:mean(), horse:std())好的,现在让我们看看神经网络的分类结果:
print(classes[testset.label[100]])
itorch.image(testset.data[100])
predicted = net:forward(testset.data[100])
-- 网络的输出是概率的对数, 要将它们转换为概率,必须采用e^x
print(predicted:exp())您可以看到网络预测。 在给定图像的情况下,网络为每个类分配概率。
为了更清楚显示,让我们用其类名标记每个概率:
for i=1,predicted:size(1) do
print(classes[i], predicted[i])
end一个样本可能很糟糕,让我们看看一个测试集中总共有多少是正确的?
correct = 0
for i=1,10000 do
local groundtruth = testset.label[i]
local prediction = net:forward(testset.data[i])
local confidences, indices = torch.sort(prediction, true) -- true表示按降序排序
if groundtruth == indices[1] then
correct = correct + 1
end
end
print(correct, 100*correct/10000 .. ' % ')看起来这大大好于随机,毕竟随机是10%的准确性(从10个类中随机挑选一个类)。 神经网络似乎学到了一些东西。
嗯,让我们看看10个类中哪些表现好,哪些表现差:
class_performance = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
for i=1,10000 do
local groundtruth = testset.label[i]
local prediction = net:forward(testset.data[i])
local confidences, indices = torch.sort(prediction, true) -- true表示按降序排序
if groundtruth == indices[1] then
class_performance[groundtruth] = class_performance[groundtruth] + 1
end
end
for i=1,#classes do
print(classes[i], 100*class_performance[i]/1000 .. ' %')
end好的,接下来呢? 我们如何在GPU上运行这个神经网络?
cunn:使用CUDA的GPU上的神经网络
require 'cunn';这个想法非常简单。 使用神经网络,并将其转移到GPU:
net = net:cuda()此外,将损失函数转移到GPU:
criterion = criterion:cuda()接下来是数据:
trainset.data = trainset.data:cuda()
trainset.label = trainset.label:cuda()好吧,让我们在GPU上训练。
trainer = nn.StochasticGradient(net, criterion)
trainer.learningRate = 0.001
trainer.maxIteration = 5 -- 只训练5轮
trainer:train(trainset)因为目前示例的网络很小,所以不考虑与CPU相比的MASSIVE加速。