DFS——组合与排列

引子

1.关于深搜：深度优先搜索是一种解决问题的算法策略。通常，首先它把问题解决过程分解成若干个阶段，然后递归地搜索(枚举)每个阶段所有可能的选项，得到组合式的解，到达边界后，检验解的合法性。
2.学习了那么久的深搜，再回头看一下，就是一串格子，按照题目的要求去填空，其本质就是求组合与排列。
3.算法框架：

void dfs(int i)
{
    if(满足边界条件)
    {
        输出解
        return;
    }
    for(可选择的选择j)
        if(没有访问过j&&其它条件)
        {
            标记j已经访问过
            保存
            dfs(i+1);
            取消标记//回溯
        }
}

正题

排列

生成n维向量vector

n维向量是有n个元素的序对，每个元素的取值范围从1到k。例如3的5维向量为{1,1,1,1,1}，{1,1,1,1,2},….,{3,3,3,3,3}。输入k和n，输出所有k的n维向量。  、
限制条件 ：1<= k <=10, 1<=n<=6

分析

简单的一个搜索，直接用框架解决，而且元素可以重复，不用标记

#include
#define MAXN 6
int n,k,a[MAXN+5];
void dfs(int i)
{
    if(i>n)
    {
        for(int j=1;jprintf("%d ",a[j]);
        printf("%d\n",a[n]);
        return ;
    }
    for(int j=1;j<=k;j++)
    {
        a[i]=j;
        dfs(i+1);
    }
}
int main()
{
    scanf("%d %d",&n,&k);
    dfs(1);
}

思考

1. 这道题如果要输出序号，可以增加一个变量tot，like this:

#include
#define MAXN 6
int n,k,a[MAXN+5],tot;
void dfs(int i)
{
    if(i>n)
    {
        tot++;
        for(int j=1;jprintf("%d:%d ",tot,a[j]);
        printf("%d\n",a[n]);
        return ;
    }
    for(int j=1;j<=k;j++)
    {
        a[i]=j;
        dfs(i+1);
    }
}
int main()
{
    scanf("%d %d",&n,&k);
    dfs(1);
}

2.k的n维向量的总方案数是多少？

对于每一个位置i，都有k个选择，一共n个位置，所以方案数应是k^n

全排列

输入n，输出数字1..n的所有排列。这里不是要计算排列有多少种，而是枚举所 有的排列，以字典顺序枚举。 
限制条件 1<=n<=10

分析

与第一题类似，要标记判重
也可以在存储的答案中查找一遍有无使用选项j,但此方法明显慢得多

#include
#define MAXN 10
int ans[MAXN+5],n;
bool vis[MAXN+5];
void dfs(int x)
{
    if(x>n)
    {
        for(int i=1;iprintf("%d ",ans[i]);
        printf("%d\n",ans[n]);
        return;
    }
    for(int i=1;i<=n;i++)
        if(!vis[i])
        {
            vis[i]=1;
            ans[x]=i;
            dfs(x+1);
            vis[i]=0;
        }
}

int main()
{
    scanf("%d",&n);
    dfs(1);
}

还有一个方法：交换法
初始：将ans数组赋成1,2,…,n
递归参数x：每次将i从x枚举到n
交换ans[x]和ans[i]
递归x+1
换回ans[x]和ans[i]

#include
#include
using namespace std;
# define MAXN 100
int ans[MAXN+5];
int n;
void dfs(int x)
{
    if(x==n)
    {
        for(int i=0;iprintf("%d ",ans[i]);
        puts(" ");
        return ;
    }
    for(int i=x;i1);
        swap(ans[i],ans[x]);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i1;
    dfs(0);
    return 0;
}

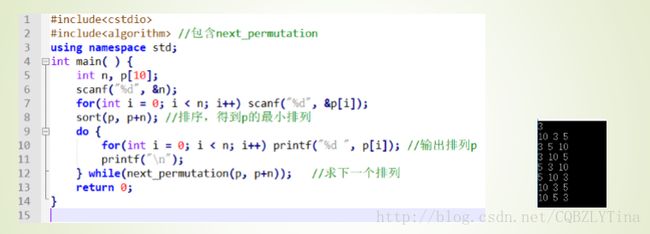
生成下一个排列：next_permutation

STL 的next_permutation()提供了便捷的枚举排列的方法。它从字典序最小的排 列开始，调用一次，产生下一个排列。 
遵从STL算法库的惯例，next_permutation(begin, end)接受两个迭代器参数，
输入和结果均在迭代器所指容器(通常是vector或数组)。 
当能够产生一个按字典序的新排列时，next_permutation()返回true，否则返
回false。可以利用返回值，在一个循环中，生成所有排列。 
调用一次next_permutation()的时间复杂度为：O(n)，大约是从当前排列到下 一个排列需要调用交换函数swap()的次数。 
另一个成对的函数是prev_permutation()，它生成上一个排列。

举个栗子：

生成可重集的全排列

输入一个包含n个整数的数组，元素可以重复。按字典序输出所有全排列，方案不重复。 
例如{1,2,2} 所有的排列就是{1,2, 2}、{2, 1, 2} 、 {2, 2, 1} 。 
限制条件 1<=n<=10 

分析

如果还像之前那样进行标记的话，由于有重复的元素，所以可能会造成重复（标记下标）或缺少元素（标记值），所以要进行去重。那我们就要思考在什么情况下是重复的。如果当前数字与上一次这个位置的数字的值是相同的，那么排列看起来没有区别，所以我们可以用一个变量last来记录上一次这个位置出现的值，进行判断。在做这个方法时要注意先排序，其目的是把相同元素排在一起，否则last会失去作用，因为last仅仅记录的是上一次的值。

#include
#define MAXN 20
using namespace std;
int a[MAXN+5],ans[MAXN+5],n,last;
bool vis[MAXN+5];
void dfs(int i)
{
    if(i>n)
    {
        for(int j=1;jprintf("%d ",ans[j]);
        printf("%d\n",ans[n]);
    }
    last=-1;
    for(int j=1;j<=n;j++)
        if(!vis[j]&&a[j]!=last)
        {
            ans[i]=a[j];
            vis[j]=1;
            last=a[j];
            dfs(i+1);
            vis[j]=0;
        }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    dfs(1);
}

第二种方法是改进一下vis[]，用一个cnt数组来记录这个数字有多少个，用去一个就–，如果cnt[i]为0，表示i已经用完了。

#include
#define MAXN 10
#define MAXVAL 30
int n;
int ans[MAXN+5];
int cnt[MAXVAL+5];
void dfs(int i)
{
    if(i>n)
    {
        for(int j=1;jprintf("%d ",ans[j]); 
        printf("%d\n",ans[n]);
        return;
    }
    for(int j=1;j<=MAXVAL;j++)
        if(cnt[j])
        {
            cnt[j]--;
            ans[i]=j;
            dfs(i+1);
            cnt[j]++;
        }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int t;
        scanf("%d",&t);
        cnt[t]++;
    }
    dfs(1);
}

第三种方法，理解为交换法中如果交换的两个数字是相同的，则没有区别

Part：组合

枚举组合Combination

枚举组合就是生成n个元素的各种组合方式。本质上说，就是枚举子集。
例如{1,2,3} 所有的组合就是{} 、 {1} 、 {2} 、 {3} 、 {1,2} 、 {1,3} 、 {2,3} 、 {1,2, 3}，一共有8 个组合

位向量法

计算组合个数的方法
1 可取可不取，有两种情形、 2 可取可不取，有两种情形、 3 可取可不取，有两种情形。根据 乘法原理，总共2×2×2 = 2^3 种情形。
用程序实现时，模拟这个过程。设立标记数组vis[]，vis[i]=true，表示集合中包含第i个元素。在 DFS中依次考虑每个元素，取还是不取，把决策信息记录在vis[]中。到达边界后，扫描vis[]，输 出一组解。
算法思想是：依序枚举每个位置。针对每个位置，试着填入取或不取

实现

#include MAXN 10
bool vis[MAXN+5];
int A[MAXN+5];
int n;
void dfs(int i)
{
    if(i>=n)
    {
        for(int j=0;jif(vis[j]) printf("%d ",A[j]);
        puts("");
        return ;
    }
    vis[i]=0;
    dfs(i+1);

    vis[i]=1;
    dfs(i+1);
    vis[i]=0;
}

增量法（能实现字典序）

思路是往子集里不断放入新元素。每次递归进入后，当前子集都是一个合法解， 先输出解。再考虑试着往子集里新增一个元素。子集里的元素应该升序生成，避免{1,2}，{2,1} 这种重复，故设立变量i指示新增元素的最小值。
增量法生成的组合是按字典序排列的。
实现

#define MAXN 10
int S[MAXN+5];
int n;
void dfs(int i,int sz)
//i:下一次放入子集的最小值  sz:当前子集的大小
{
    for(int j=0;jprintf("%d ",S[j]);
    puts("");
    for(int j=i;j<=n;j++)
    {
        S[sz]=j;
        dfs(j+1,sz+1);
    }
}

思考
把枚举子集中的元素看成是下标，就可以输出元素值为任意类型的组合。
输入任意类型的元素，存放在数组A中。先排序。
再把输出子集的语句修改成输出特定元素：

for(int j = 0; j < sz; j++) 
      printf("%d ", A[S[j]]);

二进制（位运算）法

把十进制数0~15写成二进制形式：
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
把数位从右往左分别看成是第0，1，2，3个元素，二进制数该位为0，表示该元素不在子集中； 为1，表示在子集中。例如，0110表示第1，2号元素在子集中，0，3号元素不在子集中。
从0到15正好有16个数，而包含4个元素的所有组合的个数也是16，每一个数就 对应了一个子集，该整数中1的位置就指示了属于子集的元素。
因此一个循环就可以枚举出n个元素的所有组合：

 up = 1 << n;     //up -1的二进制形式恰好有n个1 
 for(int s = 0; s < up; s++)   

要检验一个整数所代表的子集中有哪些元素，需要用到位运算：

1<//表示把1左移i位  
s & (1<//表示检验s的右起第i位是否为1，为1则表示第i号元素在子集中  
for(int i = 0; i < n; i++)  
    if( s & (1 << i)) 
         printf(“%d “, A[i]); //输出第i号元素

实现

#include
#define MAXN 10
int A[MAXN+5];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=0;iscanf("%d",&A[i]);
    int up=1<for(int s=0;sfor(int i=0;iif(s&(1<printf("%d",A[i]);
        puts("");
    }
    return 0;
}

思考
二进制法没有用到递归。
联想集合的二进制整数表示

---

Tip：内容相照应《算法竞赛入门经典》中第七章