【算法笔记】求给定序列的第k大（权值线段树/直接离散化）

普通线段树的叶子节点（最下面一层，从左到右的编号i依次是1，2，3..n）记录的是a[i]，即给定的序列值

权值线段树的叶子节点i对应的cnt[i]记录的是序列去重后第i小的数出现的次数，对于给定的序列需要离散化确定大小

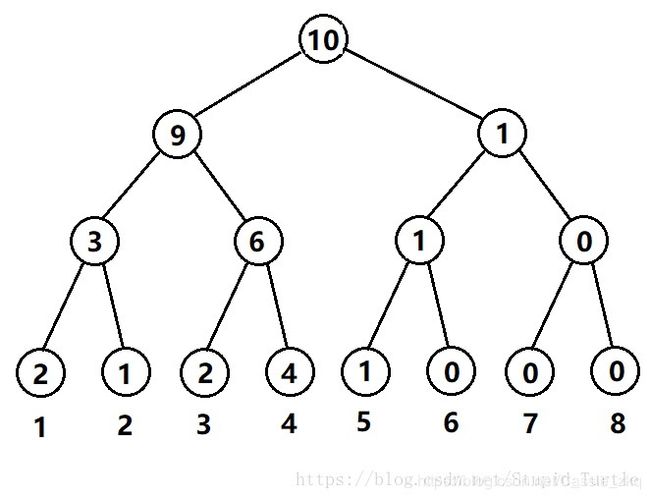
如序列：[1,1,2,3,3,4,4,4,4,5]，对应的权值线段树为：

图中第二层的9表示序列中的前9小的数都在上一个节点的左子树，1表示第9+1-第10小的数都在上一个节点的右子树，其他同理。

（图源https://blog.csdn.net/Stupid_Turtle/article/details/80445998）

---

权值线段树法：（整体二分查找）

测试样例：

7
3 3 2 1 5 5 7

#include 
using namespace std;
const int maxn = 300005;
int a[maxn], b[maxn], cnt[maxn];
void update(int id )
{
    cnt[id] = cnt[id << 1] + cnt[id << 1 | 1];
}
void build(int l, int r, int id, int no)
{
    if(l == r)
    {
        cnt[id]++;
        return ;
    }
    int mid = (l + r) >> 1;
    if(no <= mid) build(l, mid, id << 1, no);// 单点
    else build(mid + 1, r, id << 1 | 1, no);
    update(id);
}
int query(int l, int r, int id, int k)
{
    if(l == r)
    {
        return l; //返回1-n的第k大的数是去重之后的第几大数
    }
    int mid = (l + r) >> 1;
    if(k <= cnt[id << 1])
        query(l, mid, id << 1, k);
    else query(mid + 1, r, id << 1 | 1, k - cnt[id << 1]);//!k - cnt[id << 1]
}
int main()
{
    freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        b[i] = a[i];
    }
    sort(a + 1, a + 1 + n);
    int m = unique(a+1, a+1+n) - (a+1);
    for(int i = 1; i <= n; i++)
    {
        int no = lower_bound(a+1, a+1+m, b[i]) - a; //去重后第几大
        build(1, n, 1, no);
    }
    for(int i = 1; i <= n; i++)
    {
        int id = query(1, n, 1, i);
        cout << a[id] << endl;
    }

    return 0;
}

离散化法：直接copy过来了，懒得改了。

#include 
#include 
#include