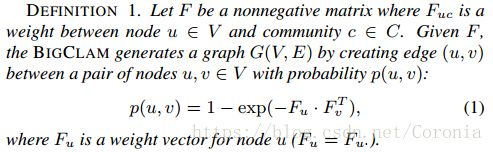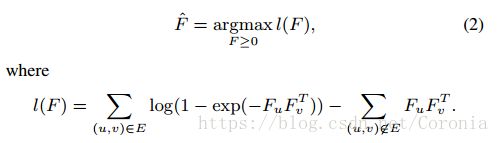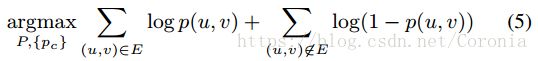读书笔记：Overlapping Community Detection at Scale: A Nonnegative Matrix Factorization Approach

​​​​​​本文是对在2013年ACM大会上发表的一篇论文所做的读书笔记，原文可以查看：

https://www.researchgate.net/publication/262272761_Overlapping_community_detection_at_scale_a_nonnegative_matrix_factorization_approach

 

文章概述

         社团指的是网络中一部分相互关联密切的顶点。同一个顶点可能会与多个顶点群体关联密切，即属于多个社团。这样即造成了社团的重叠，而要在这些重叠社团之中进行社团检测则成为了一件困难的事。本文提出了一种新的用于重叠社团检测的方法，简称BIGCLAM。与现有的社团检测方法相比，BIGCLAM对于大型网络中的密集重叠社团尤为有效。本文将会说明该方法的原理，并提供实验证明来展示该方法的有效性。

 

关于作者

Jaewon Yang曾是斯坦福大学Infolab实验室的应用研究科学家，研究领域为社团检测、矩阵分解及其应用，例如模式挖掘和推荐系统。[1]

Jure Leskovec是斯坦福大学的计算机科学副教授，也是现任的Infolab实验室成员。他的研究领域主要为大规模网络。[2]

 

研究背景

 

2.1 相关概念

 

2.1.1 社团

         网络中的社团（community）指的是一部分联系紧密的顶点（node）；而相对的，一个社团中的顶点与该社团以外的顶点之间的联系就没有如此的紧密了。这就好比人的社交圈，同属于一个圈之中的人关系肯定更为密切，而处于圈外的人则不是。

社团有时候又会被称为模块（module）或聚类（cluster），但我查到的资料显示这两者并不完全一致：社团检测侧重于找到网络中联系紧密的部分，而经常忽略节点的属性（attributes）；而聚类侧重于找到一堆属性相似的目标，从而忽略了目标与目标之间的联系。但是，两者也不是完全独立的，比如说当顶点属性未知时，就可以通过将顶点之间的关系构成邻接矩阵的方式，即用聚类的方式来完成社团检测。[3]

 

2.1.2 社团检测及其应用

社团检测（community detection，又译作社区发现）顾名思义，指的就是从网络中找出关联紧密的顶点。这里的问题在于如何定义“关联紧密”。通过查资料得知有三种主要的度量方法：基于成对计数，取决于两种划分X,YX,Y中将顶点对划分在同一个社团的顶点对的数量；基于聚类匹配，找出不同划分中社团的重叠性；基于信息论，根据香农信息熵理论进行计算不同划分之间的相关性。[4]

社团检测在各个领域都有应用价值：在社交软件开发领域，社团检测可以用于挖掘用户之间的潜在关系；在生物研究领域，可以用于检测蛋白质复合体的结构；即使是对于真实的互联网，社团检测也可以用于挖掘相关的网站。[5]在当今的大数据时代，面对如此庞大的网络，能够在其中进行有效的社团检测就等于抓住了先机。

 

2.2 问题描述

        

         目前，社团检测主要面临的问题除了数据量、网络的极速扩大之外，还有就是本文主要探讨的重叠（overlap）现象。重叠指的是同一个顶点同时与两个以上的顶点群体关系紧密，即同属于多个社团。同样拿社交关系来类比，就相当于一个人可以加入多个现实中的社团。根据重叠部分的顶点数量以及与其他顶点的联系，我们可以判断其重叠的稠密程度，并用图像来表示这些社团之间的重叠情况：

         显然，这些重叠的部分对于社团检测来说并不利。大多数的社团检测方法只适用于将一个顶点归类到一个社团之中，因此面对重叠社团时就容易出现偏差，或是结果不准确。要想对这些重叠的顶点进行有效的检测，就需要针对重叠社团的情况开发专门的新方法。

 

2.3 现有方法比较

         我查到了一些在新的社团检测方法提出之前（2013年），已有的社团检测方法：

 

2.3.1 LOUVAIN

         基于模块度（Modularity）的社团检测算法，其中模块度指的是社区内紧密程度的值Q。该算法较为简单，且不需要监督，运行速度也较快。缺陷则在于缺乏监督导致的难以评判聚类效果的好坏。[6]该算法也没有对重叠社团问题进行解决。

 

2.3.2 Infomap

         基于信息论的算法，使用随机游走作为网络上信息传播的代理，网络上的随机游走会产生相应的数据流。随机游走产生的信息量使用平均一步随机游走产生的码字长度衡量，即平均码字长度。[7]该算法思路较为创新，效果也比较好。而且该算法的改进型也可用于重叠社团检测，不过我没有查到更多的资料。

 

2.3.3 GCE

         贪婪小团体扩展（Greedy Clique Expansion，GCE）：识别不同的小团体作为种子，通过优化本地适应性函数贪婪扩展这些种子。该算法是LFK算法的改进，解决了LFK对于某些特殊种子循环扩充而无法停止的问题。该算法可用于进行重叠社团检测，改进方式为根据经验来设定a因子以及引入并行计算来加快运行速度等。[8]

 

2.3.4 Clique

         CLIQUE算法是一种基于网格的聚类算法，用于发现子空间中基于密度的簇。该算法首先判断是不是密集网格，如果是密集网格。那么对其相邻的网格进行遍历，看是否是密集网格，如果是的话，那么属于同一个簇。该方法可以划分出重叠的社团，但对于高维数据，基于网格的聚类倾向于效果很差。[9]

 

         上述的这些方法各有优劣，但在规模庞大的网络中检测重叠社团时都会显得捉襟见肘。因此，本文便提出了专门用于解决这一情况的BIGCLAM算法。

 

 

BIGCLAM

 

3.1 概念

         BIGCLAM（Cluster Affiliation Model for Big Networks，大型网络的聚类关系模型）是一个bipartite affiliation network模型。关系网络已经被广泛运用到社会学研究中，其主要思想是同一个社团中的成员应该会有共享的关系，因此整个网络就由这些双边关系为基础来进行构建。BLGCLAM将社区检测视为非负矩阵分解（nonnegative matrix factorization），而且与NMF相似的，需要在网络中找到能还原这个邻接矩阵的因子。

         但是相对于传统的NMF，BIGCLAM做出了两个改进：首先，大多数NMF方法对潜在因素的关注度较低，而主要致力于恢复矩阵的缺失值。相比之下，BIGCLAM网络则会去学习这些影响关系网络的潜在因素；其次，BIGCLAM优化了解释模型关联的算法，这使得其有着在接近常数时间复杂度内计算出因子矩阵的可能性。而现在大部分NMF算法的时间复杂度为线性，在实际测试中BIGCLAM算法的训练速度可以比它们快出1000倍。

         该方法可扩展性强，足以处理一个有着80万个顶点和280万条边的手机网络的重叠社团检测问题；而相对较为简单的非重叠社团检测方法也已被运用于百万顶点级别的网络。总而言之，BIGCLAM方法可以极大提升大型网络中社团检测的效率和准确度。

 

3.1.1 非负矩阵分解

         我也查了一下非负矩阵分解的相关资料。NMF的基本思想可以简单描述为：对于任意给定的一个非负矩阵A，NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V，使得满足 ，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。

NMF分解算法具有实现上的简便性、分解形式和分解结果上的可解释性，以及占用存储空间少等诸多优点。为高效处理这些通过矩阵存放的数据，一个关键的必要步骤便是对矩阵进行分解操作。通过矩阵分解，一方面将描述问题的矩阵的维数进行削减，另一方面也可以对大量的数据进行压缩和概括。[10]

 

3.2 经验观测

         作者在进行BIGCLAM的研究时，第一步便是先对拥有确定社团结构的网络（ground-truth communities）进行观察，找出社团中顶点的共同因子。这种方法虽然只是凭经验直觉，但也为接下来的进一步研究提供了基础。

         作者选择了6个现有的大规模社交信息网络来进行观察：

         6个网络都是当今流行的网站，这里不详细介绍。它们都有着成千上万，甚至数百万个顶点，并且拥有重叠社团的稠密边特性。在作者之前的研究中，已经证实了这些网络是有可靠性和鲁棒性的，即经验观测的结果可以与真实结果保持相对一致。

         补充说明一点：关于这6个网络的可靠性，已经在作者之前的论文中进行了论证[11]。这些网络也已经公开发表在斯坦福大学的网站上：http://snap.stanford.edu/data

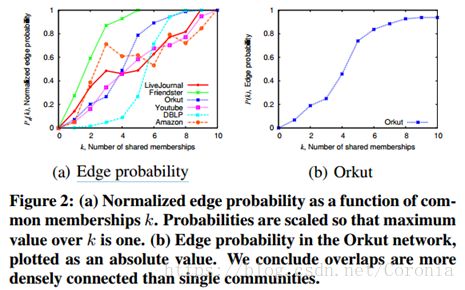
         也可以用折线图来表示这些网络的共同社团关系与其边的连接概率之间的函数关系，图表显示两者基本上成正相关：

         初步结论：一般情况下，重叠社团图中的边，即顶点之间的相互关系更为紧密。这一点在现实中的社交网络以及医疗中的蛋白质结构网络等地方也有直观的体现。

 

3.3 聚类关系模型（Cluster Affiliation Model）

 

3.3.1 顶点之间的关系

         根据上面的观测结果，作者开始构建BIGCLAM网络。网络的模型与三个因素相关：

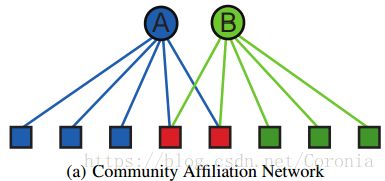
• 基于R. L. Breiger的研究成果[12]，用bipartite affiliation network模型来表示顶点与共同关联之间的网络关系，即网络由关系本身起始，连向被包含在其中的顶点：

 

• 为顶点赋值权重，权重越高代表越有可能与社团中的其他成员相连。
• 事实证明，如果两个顶点同时属于多个相同的社团，那么它们之间相连的可能性就更大。

上述的三种因素可以用来描述许多网络的模型，例如下图表示了网络中顶点在非重叠、重叠和包含社团情况下所对应的网络模型：

        

3.3.2 构建网络的边

接下来，我们把关注点由顶点放到边上来。若要对双边社团关系B（V，C，M）生成一个网络模型G（V，E），我们就需要明确G对于关系B生成边E的过程。

以下部分涉及大量计算，比较难懂，因此会挑些自己能够看懂的来写。

 

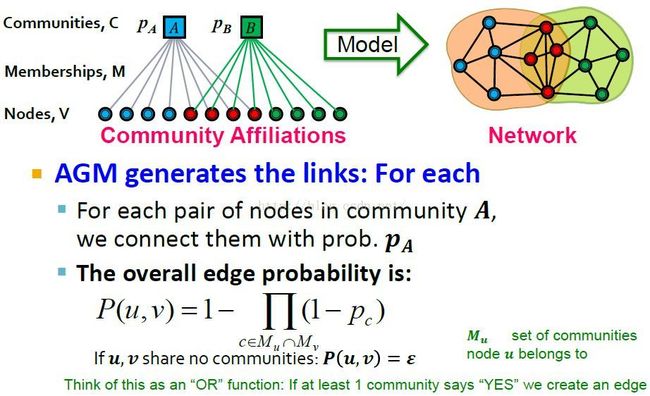
每个社团C创建的边是独立的。但是，如果一对顶点被连接多次的话，重复的边将不会包含在图G（V，E）中。由于每个社团以独立概率1 - exp（-Fuc·Fvc）来连接顶点u，v，u和v之间的边缘概率即为1 - exp（-∑c Fuc·Fvc）并随着共享社团的数量而增大。

此处定义了在顶点u，v之间创造边的概率P（u，v）的表达式：

 

3.3.3 ε社团

         上述定义中的概率公式导致的一个后果是：BIGCLAM网络不会让不属于任何相同社团中的两个顶点u，v之间连结。为了解决这一弊端，可以构建另一个社团（即ε社团），其中包含了任何连结概率不小于ε的顶点对u和v。在作者的实验中将其设置为ε ≈ 10−8。

 

3.4 社团检测

         现在网络模型已经建立完毕，现在来解释它是如何进行社团检测工作的。对于一个未进行标记的无向网络G（V，E），要检测其社团，即使得可能性l(F) = log P(G|F)最大化：

 

3.4.1

我们先假设社团数量K已知，稍后再说明如何估计K的数值。上述提到的最优解问题可以转化为NMF，将- l(F)用损失函数D和连接函数1−exp(·)表示，上式转化为： 。

使用NMF的优点在于可以提高可扩展性，BIGCLAM则进一步做出了改进。NMF一般使用l2范数来作为损失函数，而这对于二元判断来说并不是最优的。BIGCLAM改为使用log-代价函数，这使得运算时间缩短到接近常数级别。

接下来就用BIGCLAM方法来求解这个最优解问题。采用投影梯度上升法（projected gradient ascent），其中梯度为： 。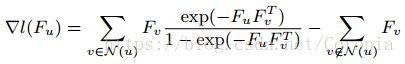

 

这里额外补充一点：我们一般在机器学习里，接触到的都是梯度下降法，那么这个梯度上升法又是怎么回事呢？查找资料得知，梯度上升法是求函数的局部最大值。算法的迭代过程是一个“上坡”的过程，每一步选择坡度变化率最大的方向往上走，这个方向就是函数在这一点梯度方向。所谓的梯度“上升”和“下降”，一方面指的是你要计算的结果是函数的极大值还是极小值。计算极小值，就用梯度下降，计算极大值，就是梯度上升；另一方面，运用上升法的时候参数是不断增加的，下降法是参数是不断减小的。但是，在这个过程中，“梯度”本身都是下降的。[13]

 

回到论文上来，经过一系列计算后，我们把F投影到了一个非负矩阵空间中。在大型的网络中，这样的计算一般来说是很费时的，但我们可以通过改进计算方法来让时间复杂度降低到O(|N (u)|)。具体如何改变的不是很理解，这里就不写了。

 

3.4.2

在解决了最优解问题，即学习了对应的社团信息后，还需要判断某个顶点u是否属于这个社团之中。我们可以设置一个下限δ，当计算出的F低于该值时就判断其不属于。设置的具体过程如图（反正我没看懂）：

之后还需要初始化F，可以使用逻辑最近邻算法。对于逻辑最近邻k中的顶点u’，我们初始化Fuu’为1，否则设为0。

 

3.4.3

         下面回到求解K的问题上来。可以将顶点集合划分为两部分：用80%的顶点来进行网络的训练，然后用剩下的20%来进行验证。这里的K值相当于一个参数，我们的目的就是找到使测试集社团检测准确率最高的K值。

 

3.5 BIGCLAM与AGM的比较

         最后，作者比较了BIGCLAM与其他关系网络模型，以AGM为例。AGM即社团隶属关系图模型（Community-Affiliation Graph Model），可以说是BIGCLAM的基础。其模型可以表示如下：[14]

         BIGCLAM作为AGM的松弛版本，改进之处在于增加了边权重，采用了NMF方法等。和BIGCLAM一样，AGM也需要进行边概率的最优解求解问题，其求解公式为：

         与BIGCLAM相比，AGM的最优解问题就显得十分难以求解了。但作者随后证明了BIGCLAM方法可以由弱化AGM的最优解问题来导出，证明过程略（看不懂）。

 

实验

接下来，作者通过对比实验来证明了BIGCLAM方法的高效性和有效性。具体方法是使用BIGCLAM方法以及其他社团检测方法，对各种不同领域的网络进行社团检测。

 

4.1 Synthetic networks

作者采用了synthetic networks（没查到中文名）来验证BIGCLAM的收敛性和扩展性。

首先验证收敛性能，通过AGM生成100个synthetic networks，之后让BIGCLAM来复原其社团关系状况。实验结果表明，BIGCLAM有98%的概率成功重构网络，且准确率较高（F1-Score高于0.85）。而在27%的测试情况中，F1-Score高于0.95，即重构的网络几乎完美。这说明BIGCLAM可以很好地将网络收敛到正确的社团上。

我也去查了一下F1分数的资料。F1分数又称平衡F分数（balanced F Score），它被定义为精确率和召回率的调和平均数。人们通常使用准确率和召回率这两个指标，来评价二分类模型的分析效果。但是当这两个指标发生冲突时，我们很难在模型之间进行比较。F分数的物理意义就是将准确率和召回率这两个分值合并为一个分值，在合并的过程中，F1分数认为召回率和准确率同等重要。[15]

 

接下来验证可扩展性，即BIGCLAM随着网络增大的表现。本次实验取了多个其他算法作为对照，包括NMF、Link Clustering、Cirque、MMSB和没有求解优化问题的BIGCLAM。其中，NMF和Cirque上文已经提到过；Link Clustering属于分级聚类方法，即连续不断的将最为相似的两个群组合并，来构造一个新的群组；MMSB也是一个用来表示关系网络的框架模型。这些方法可以说是在BIGCLAM提出前最为优秀的算法之一。

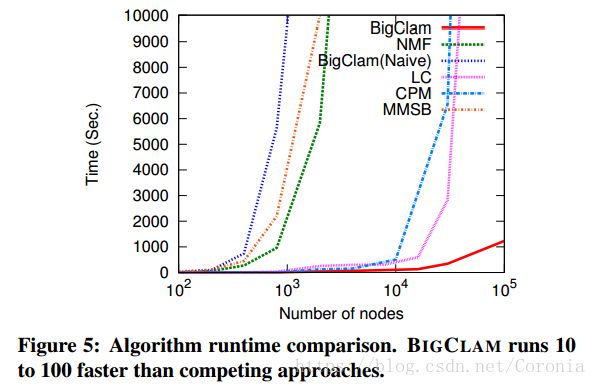
这些算法随着网络大小增大，所需要的运行时间如下图：

显然，BIGCLAM在顶点数量增大时，所需运行时间的增大速率小于其他算法。这就说明了BIGCLAM足以处理大型网络，可扩展性强。

 

4.2 用已知的社团来作为测试集

         这个实验的目的是为了验证BIGCLAM的准确性。由于大部分算法难以处理大型网络，所以需要从上述的六个大型网络中取子图，以使得其他算法可以适用，方便比较BIGCLAM和它们的性能。以Cirque、聚类算法和MMSB的运行结果作为基准。由于测试集的社团数量已知，所以我们可以量化检测结果，具体包括如下评判标准：

         平均F1分数：

         Omega Index，这是用来评判每对顶点共享的社团数的检测精确度的分数：

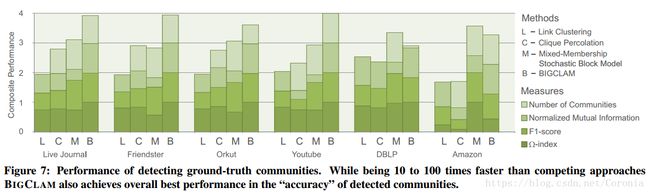
此外还有归一化互信息（Normalized Mutual Information）以及命中率等标准。BIGCLAM和其他算法对上述的六大网络中的同一子图进行社团检测的结果跑分如下：

         图像显示，BIGCLAM在大部分情况下比其他三种社团检测算法拥有更好的性能。但同时我们也注意到对于DBLP和亚马逊网络，MMSB显得更胜一筹，而BIGCLAM总是在某一个评判标准下表现不佳。这是因为BIGCLAM只会采用一个参数来求解所有的成边概率，而MMSB则会对每条边采用一个独立的参数，因此可以更好地拟合原网络。

 

4.3 Ahn et al 没看懂

 

4.4 大型网络实验

         在本次实验中，之前的几种对照算法将不再适用。因此，我们以另外两种著名的图像划分方法Metis和Graclus作为参照标准。这两种方法在网上可以查到一些现成的源码，这里不详细进行探讨。

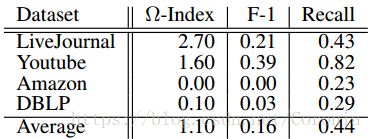
         同样，我们使用F1分数、Omega Index和归一化互信息来评判网络的性能。由于这些网络中包含了部分不能表示其所属社团特征的顶点，我们需要使用平均召回率来评判这些点能否被准确检测：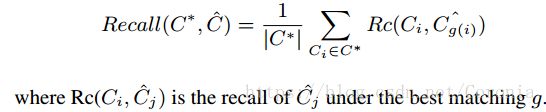

         由于Metis和Graclus算法的表现十分相似，对于每个评判标准，我们选择它们之中最好的来与BIGCLAM进行比较，比较结果显示了对于每个评判标准，BIGCLAM相比两种旧算法提升了多少，如下表：

         总的来说，BIGCLAM在各项测试中都能获得比基准算法更高的跑分，无论是在效率还是准确率上，BIGCLAM的表现都十分出色。

 

总结

 

5.1 读后感

         这篇文章阐述了BIGCLAM这种新型的社团检测算法的原理和作用，并证明了它是确实是高效而有效的。随着如今数据量的增大，网络的规模也越来越大，其包含的“重叠社团”也越来越多。原有的算法正在逐渐过时，急需新的替代品。BIGCLAM在原有的NMF和AMG方法上加以改进，使其拥有了更好的性能，这不得不说是一种创新。人工智能领域的更新换代是极为迅速的，要想赶上潮流，就需要不断去了解和学习当今的先进知识中，并在此基础上推陈出新。这两位作者所拥有的不仅仅是创新精神，在学术研究精神和坚持精神上也可以说是很好的榜样了。对于重叠社团检测这一课题，他们还另外发表了三篇其他论文，并持续研究了一年多。这三篇论文我在写读书笔记时也有去看过，在内容上可以说构成了递进关系：同样的6个大型网络，首先总结出一套规律，然后换用不同的方法去进行尝试，最终开花结果得出BIGCLAM这一方法，这其中经历的辛劳自然是不会少的。通观这些论文还可以发现，作者对学术的态度极为严谨，不仅仅是详细记录下了各种数据，还会针对研究中遇到的某些问题进行分析和实验验证。所以说，在学术研究领域，光有idea还是不够的，更需要脚踏实地去进行切实的研究。

 

5.2 改进方案

         本文可以说一直在描述BIGCLAM有多么强悍，那么它是否真的没有弱点了呢，又是否有进一步改进的余地？不过我自己也想不到什么好的点子，只好去查找了这方面的资料。

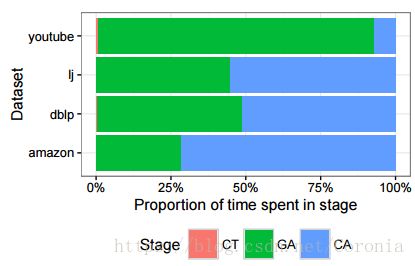
         2017年的一篇论文[16]指出，BIGCLAM的计算步骤可以概括为三步，即上面提到的初始化社团（Conductance Test，简称CA）、梯度上升求最优解（Gradient Ascent，简称GA）以及实际的社团关联检测（Community Association，简称CA）。下图显示了BIGCLAM在对不同的网络进行社团检测时三个阶段的耗时比：

        

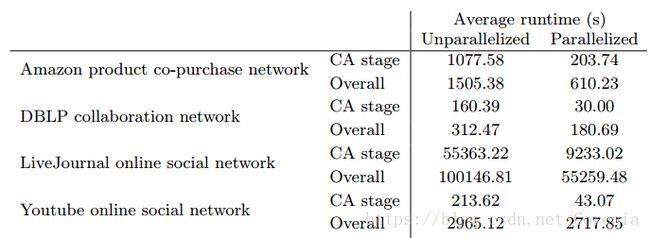
可以看出，最后的检测阶段占用的时间最长，因此该论文尝试用并行计算去求解这一阶段。他们进行了如下工作：首先证明这三个阶段的存在以及第三阶段用时最多，然后提出并行求解的方法，最后证明这种方法的有效性。具体的研究流程不详述，结果证明社团检测阶段的运算确实可以通过并行计算来进行优化：

 

 

 

 

参考资料：

[1] Jaewon Yang: http://infolab.stanford.edu/~crucis/

[2] Jure Leskovec的个人主页: https://cs.stanford.edu/~jure/

[3] 社团检测（Community Detection）和聚类（Clustering）: https://blog.csdn.net/u012854831/article/details/78301748

[4] 社团检测度量指标: https://blog.csdn.net/DreamHome_S/article/details/78369621

[5] 复杂网络社团检测算法及其应用研究: https://max.book118.com/html/2017/0509/105530857.shtm

[6] Louvain社区发现算法: http://www.cnblogs.com/allanspark/p/4197980.html

[7] 基于信息论的社团发现算法:

https://baike.baidu.com/item/%E5%9F%BA%E4%BA%8E%E4%BF%A1%E6%81%AF%E8%AE%BA%E7%9A%84%E7%A4%BE%E5%9B%A2%E5%8F%91%E7%8E%B0%E7%AE%97%E6%B3%95/22130357

[8] 基于局部扩充与优化的重叠社群检测+算法的研究: https://max.book118.com/html/2016/0118/33491503.shtm

[9] CLIQUE:一种类似于Apriori的子空间聚类算法: https://blog.csdn.net/WOJIAOSUSU/article/details/58251769

[10] 非负矩阵分解NMF: https://blog.csdn.net/zlp_zky/article/details/78396509

[11] J. Yang and J. Leskovec. Defining and evaluating network communities based on ground-truth. In ICDM ’12, 2012.

[12] R. L. Breiger. The duality of persons and groups. Social Forces, 53(2):181–190, 1974.

[13] 梯度上升与梯度下降: https://www.cnblogs.com/hitwhhw09/p/4715030.html

[14] 社交网络之社区检测：基本技巧: https://blog.csdn.net/pipisorry/article/details/49052057

[15] F1分数: https://baike.baidu.com/item/F1分数/13864979

[16] CHB Liu, BP Chamberlain. Speeding Up BigClam Implementation on SNAP.