论文解析 - Probabilistic Data Association for Semantic SLAM（一）简介

前言

本文解析的论文是Probabilistic Data Association for Semantic SLAM，其为ICRA2017 Best Paper，来自美国宾夕法尼亚大学的Sean L. Bowman和George J. Pappas。

ICRA为机器人三大会议之一，完整名单为：IROS ICRA RSS。

该论文附带youtube视频：https://www.youtube.com/watch?v=JMkBTK9mahk，跑的是KITTI经典室外车辆运动数据集，演示的效果中建好的地图中的物体会基于当前估计的摄像头姿态被投影到观测中，作为一个观测的预测，然后以此辅助摄像头姿态的估计。

注意蓝色的车辆为地图中建立的物体模型投影到当前观测中的效果。

简单梳理文章结构，其实该论文核心就是提出了一种将尺度信息和语义信息融合的理论框架，而前端的选择则可以基于实际情况挑选，论文中挑选的是比较常用的物体检测框架。

识别语义物体，然后将其建立到地图中。

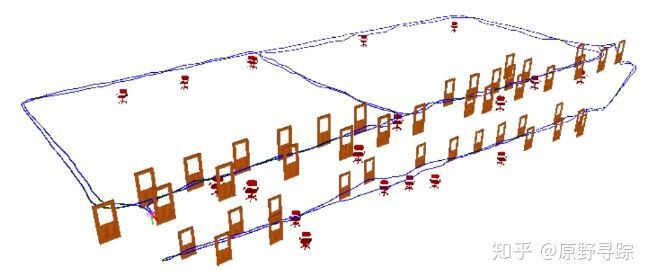
建立的地图以及轨迹。

系列解析将重点理解其数学模型，并补充理解该论文所需的几点内容，如概率图模型因子图、涉及的非线性优化相关知识等。根据论文章节可能会拆分成多个部分，论文第一部分的叙述就不说了大家可以自己看，本文作为第一篇文章重点介绍论文第二部分：SlAM中的数据关联概率学原理。下一文将介绍语义SLAM。
16年综述说：语义slam正处于婴儿期，或许此文会将其带入幼儿期。

 

---

跳过前文论述，直接进入第二部分的主题。

II. Probabilistic Data Association in SLAM

SLAM中的概率化数据关联问题

论文中对SLAM问题的数学模型做出了非常清晰的定义。在经典SLAM问题中，移动的传感器经过未知的环境，将M个静态路标建模为集合  ，给定传感器测量为集合  ，任务为估计路标位置  和传感器的姿态序列，姿态序列将反映传感器的轨迹。

而目前大部分已有的工作都忽略了一个问题，那就是数据关联  。定义 ，其意义为第k组观测 是在传感器姿态  下获得的路标  的观测。实际情况下这个数据关联是未知的，比如我们图像中看到一堆点云，然而我们无法确定是一个杯子还是一个椅子，我们只能说根据各种特征发现是椅子的概率高，所以我们当成椅子进行后面的处理。

完整状态的SLAM问题的数学模型应该是这样的：

所以这篇文章实际上在论述，引入语义信息之后，如何合理求解该数学表达式。

 

这里强调一下如何理解数据关联。

每一组D中  代表的是姿态，而  代表的是路标，这之间的关联关系是个什么意思呢。

答：代表了我手里的这个测量  是在哪里看的哪个路标。

一般的slam过程中，姿态都是估计出来的，对应的地图中的路标也是估计出来的。

所以求解的话我们需要先估计对应关系，即数据关联D，再估计获得X和L。

 

引入数据关联D后，传统SLAM问题的变化：

• 第一步：估计数据关联D的估计

• 第二步：将估计的数据关联D代入下一步估计出姿态X和路标L

注意这两步是顺序进行。这个过程有一个很大的问题，如果第一步数据关联的估计不正确，将极大影响第二步的估计性能。此外，如果模糊的测量被舍去来避免错误的数据关联，之后哪怕这些模糊测量收敛了也没有机会再考虑它们。

因此，还存在一种坐标下降法（coordinate descent）迭代计算这两步：

这个方法可以在姿态估计改善之后，重新进行数据关联的决策。但是没有解决模糊数据的处理问题，因为每一次D的估计都是一次硬决策(hard decision)。别急，看到下面就知道什么叫软决策了。

语义信息与尺度信息共同更新

为了解决这个问题，当估计X和L的时候，我们把D的整体分布也考虑到一起。最好当然是混合成一个优化问题了，作者选择的模型是期望测量似然（expected measurement likelihood），长这个样子：

给定初始估计­和  和，让这个期望测量似然取最大值的X和L即是我们所需要的下一步状态的 和。即：

 是D取值的所有可能空间，第二个等号的公式变形基于期望的意义，即让变量D的所有可能对应的概率，取乘以取该可能时获得的因变量值。该公式中因变量即  ，我们求解的目的也是获得一组  和来让 在条件给定  下的期望取得最大值。

这个公式的优点在于我们不需要强行决断一个数据关联了，比如一般来说一定要确定我这次观测到底是桌上的瓶子还是地上的椅子，从而根据瓶子和椅子在地图中的位置来估计当前观测传感器的姿态，这叫硬决策。该公式引入了软决策，即平均所有可能的数据关联。（有点像薛定谔的感觉，当前状态是瓶子和椅子的一个概率分布叠加。果然底层是相同的呀，面白い。）

而该公式求解方法是期望最大值（expectation maximization），简称EM法。它是因子图的一种常用解法，可以见补充知识点：因子图。

为了与坐标下降法的公式做对比，公式（4）可以被重写为如下形式:

其中  是一个与X、L无关的权重，衡量各部分对软数据关联的影响力。

由于最终需要用算法实现，而矩阵运算无论在代码书写还是计算效率上都是最好的方式，那么如何将式子与矩阵运算关联起来呢。论文用Proposition 1将其与矩阵行列式的值奇妙地结合在了一起:

公式具体含义在此不多叙述，论文附录中有详细证明。有了这个公式我们就可以在算法中实现了。

EM法的求解和公式（5）相似，能够以迭代的方式去求解最优估计问题。EM法一共可以分为两步：

• “E”Step：估计数据关联的概率分布  作为权重，而不是估计数据关联的极大似然（不是一个确定值，是一个分布）
• “M”Step：在前一步计算的分布基础上，最大化期望测量似然的log值

 

到这里该部分就梳理完成了，接下来对几个重点部分做一下深入。

---

重点理解

对于公式 

第一步推导到第二步推导怎么来的？其中的的含义如何理解。

论文中对做了定义，可以这么理解：第一个公式表达的是在所有数据关联的可能性下，即我观测的如果是苹果，如果是椅子，如果是水杯，都进行一次考量然后叠加。每一次考量中，计算的东西是，看到的这个点云是因为在A点看苹果的概率（  ）乘以我在A点看苹果所得到的真实观测是这个点云的概率（  ，取log仍然是正相关），真实观测是通过在地图中模拟观测点，并已知苹果的位置来计算的。

所以所有这些可能叠加之后的值将考虑了许多方面的影响，包括姿态、路标、观测，如果要想整体数值最大，即与现实情况最逼近，那么X和L将与现实情况最逼近。

基于这个道理，我们求得的X，L将是实际情况路标和传感器姿态的最优估计。

 

数学上来看，第二步和第一步也只是换了一种描述形式。本质上仍然是遍历所有组合并且求得对应概率。

---

我们应该明确一个问题，本篇文章核心目标是用语义信息辅助获得路标和摄像头姿态，也就是语义信息将在数学模型中对姿态估计造成影响。

我们的语义信息显然在目前主模型中反映在观测Z中，而观测还包含了惯性信息和里程计信息，如何将其融合将是下一节的数学模型要解决的问题。

那么下一讲将继续介绍III. SEMANTIC SLAM。

第一次写分享，有的词汇翻译可能不是很标准，欢迎指出。

语义SLAM方向目前来看是个比较小众的方向，欢迎共同学习交流。