BZOJ-1977 次小生成树 Tree 树上倍增LCA+Kruskal+位运算
char哥刚了这题一天，被我2小时拍完....
-----DaD3zZ：char哥，我们竞速吧，我觉得我能跑的比你快；
-----Char哥：写了多少行...我只有65行
-----DaD3zZ：我....148行，但我没压行！！
一会儿后....
-----DaD3zZ:char哥我A的你比快很多
-----Char哥：我刚刚又看了看，感觉能拿到40～50行左右！！！
鬼畜的压行超人char哥Etienne！！
1977: [BeiJing2010组队]次小生成树 Tree
Time Limit: 10 Sec Memory Limit: 512 MB
Submit: 2629 Solved: 643
[Submit][Status][Discuss]
Description
小 C 最近学了很多最小生成树的算法，Prim 算法、Kurskal 算法、消圈算法等等。 正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说： 如果最小生成树选择的边集是 EM，严格次小生成树选择的边集是 ES，那么需要满足：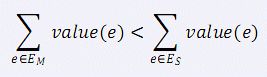
(value(e) 表示边 e的权值) 这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。
Input
第一行包含两个整数N 和M，表示无向图的点数与边数。 接下来 M行，每行 3个数x y z 表示，点 x 和点y之间有一条边，边的权值为z。
Output
包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
Sample Input
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
Sample Output
11
HINT
数据中无向图无自环； 50% 的数据N≤2 000 M≤3 000； 80% 的数据N≤50 000 M≤100 000； 100% 的数据N≤100 000 M≤300 000 ，边权值非负且不超过 10^9 。
Source
做法：
此题为严格次小生成树，所以做法有些麻烦
首先求出最小生成树
并从剩余边中依次枚举，并进行操作
将这条边加入树，形成一个环，那么删掉此环上的一条边，就会从新出现一棵生成树，那么如何高效的去找要删去的边
倍增LCA
倍增维护3个值，father【】维护LCA，f维护路径上的最大值，g维护路径上的严格次大值
维护次大的值的意义在于：
对于删环上的边，如果添加进来的边与环上最大值不同，那么直接删换上最大值，如果与最大值相同，就必须删次大值（因为删除最大值之后仍为最小生成树）（第一次忘了进行讨论了…）
那么只需要枚举每一条剩余的边来判断就好
code：
#includeint fa[maxn];
struct dat{int to,next,from,val;}road[maxn*2];
int head[maxn],tot;
//init
void add(int u,int v,int w)
{
tot++;
road[tot].to=v; road[tot].from=u; road[tot].val=w;
road[tot].next=head[u]; head[u]=tot;
}
void insert(int u,int v,int w)
{
add(u,v,w); add(v,u,w);
}
//add road
void init()
{
for (int i=1; i<=n; i++) fa[i]=i;
}
int find(int x)
{
if (fa[x]==x) return x;
fa[x]=find(fa[x]); return fa[x];
}
bool merge(int x,int y)
{
int f1=find(x),f2=find(y);
if (f1!=f2)
{fa[f1]=f2;return 1;}
return 0;
}
//kruskal
int father[maxn][25],f[maxn][25],g[maxn][25];
int deep[maxn];
void dfs(int x,int last)
{
//printf("%d %d\n",x,last);
for (int i=1; i<=20; i++)
{
if(deep[x]<(1<break;
father[x][i]=father[father[x][i-1]][i-1];
f[x][i]=max(f[x][i-1],f[father[x][i-1]][i-1]);
if (f[x][i-1]==f[father[x][i-1]][i-1])
g[x][i]=max(g[x][i-1],g[father[x][i-1]][i-1]);
else
g[x][i]=min(f[x][i-1],f[father[x][i-1]][i-1]),
g[x][i]=max(g[x][i],g[x][i-1]),
g[x][i]=max(g[x][i],g[father[x][i-1]][i-1]);
}
for (int i=head[x]; i; i=road[i].next)
if (last!=road[i].to)
{
father[road[i].to][0]=x;
deep[road[i].to]=deep[x]+1;
f[road[i].to][0]=road[i].val;
dfs(road[i].to,x);
}
}
void swap(int &x,int &y)
{
int tmp=x; x=y; y=tmp;
}
int LCA(int x,int y)
{
if (deep[x]int d=deep[x]-deep[y];
for (int i=0; i<=20; i++)
if ((1<for (int i=20; i>=0; i--)
if (father[x][i]==father[y][i]) continue;
else x=father[x][i],y=father[y][i];
if (x==y) return x;
return father[x][0];
}
int work(int x,int lca,int val)
{
int maxx1=0,maxx2=0;
int d=deep[x]-deep[lca];
for (int i=0; i<=20; i++)
{
if (d&(1<if (f[x][i]>maxx1)
maxx2=maxx1,maxx1=f[x][i];
maxx2=max(maxx2,g[x][i]);
x=father[x][i];
}
}
if (maxx1!=val) minn=min(minn,val-maxx1);
else minn=min(minn,val-maxx2);
}
void solve(int x,int val)
{
int u=edge[x].from,v=edge[x].to,lca=LCA(u,v);
work(u,lca,val); work(v,lca,val);
}
int main()
{
// freopen("mst2.in","r",stdin);
// freopen("mst2.out","w",stdout);
n=read(),m=read();
for (int i=1; i<=m; i++)
edge[i].from=read(),edge[i].to=read(),edge[i].val=read();
sort(edge+1,edge+m+1);
int cnt=0; init();
//puts("OK");
while (num1)
{
cnt++;
if (merge(edge[cnt].from,edge[cnt].to)==1)
num++,ans+=edge[cnt].val,edge[cnt].used=1,
insert(edge[cnt].from,edge[cnt].to,edge[cnt].val);
//printf("%d %d %d %d\n",edge[cnt].from,edge[cnt].to,edge[cnt].val,edge[cnt].used);
}
//printf("%d\n",ans);
dfs(1,0);
//puts("OK");
minn=0x7fffffff;
for (int i=1; i<=m; i++)
{/*printf("%d is OK\n",i);*/if (!edge[i].used) solve(i,edge[i].val);}
printf("%lld\n",ans+minn);
return 0;
} 对比图：
char哥：
自己：
YveH大爷：
居然跑的比char哥慢，不开心！！！！
不过跑的比YveH大爷快很多QAQ…
不过还好自己 边+调 用了1h+
而char哥用来1afternoon&1night+