用 Matlab 计算并画出大量数据的CDF
这篇 blog 将展示用 matlab 计算并画出大量数据的 CDF (累计分布函数)的两种方法。第一种是我自己于2012年写的,后来用的过程中发现有缺陷;后来2014年写另一篇paper时,搜寻到第二种简易又高效的方法。这里我给出它们各自的用例,包括画图用的数据与脚本,以及效果图。For your reference.
============================================================================================
Section A. 第一种方法
今天(2012-10-17)有一些数据需要处理,这些数据好不容易从文件中剥离了出来,然后自己写了一个function,计算并控制 plot 这些数据的 CDF 图。因为第一种方法用到的例子的数据文件太大,就没有贴上来。如果有想亲自试验一下这个过程的同学,请参照下文中第二个方法中的完整用例。
% ----------------------- 自实现 CDF 计算 function: funcCDF.m
% para@1: CNT_pnts, the number of points to denote the CDF;
% para@2: Range_low, the lower bound of variable;
% para@3: Range_up, the upper bound of variable;
% para@4 : arr_Vals, array of the values to be processed.
function [x, CDF_Vals] = funcCDF(CNT_pnts, Range_low, Range_up, arr_Vals)
data = sort( arr_Vals' ); % T', horizon arrays of T.
N = length(data);
stepLen = (Range_up-Range_low)/CNT_pnts;
Counter = zeros(1,CNT_pnts);
for i = 1:1:N
for j = 1:1:CNT_pnts
if ( data(1,i) <= (Range_low + j*stepLen) )
Counter(1,j) = Counter(1,j) + 1;
end
end
end
CDF = Counter(1,:)./N;
CDF_Vals = CDF(1,:)';
x = (Range_low+stepLen):stepLen:Range_up;
% ---- end of func.% --------------------- 2 use cases:
CNT_pnts = 100;
deadline_N500r1 = 550;
deadline_N500r3 = 270;
deadline_N500r5 = 240;
PntVal_N500Tau100r1 = textread('N500Tau100r1.tr','%*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %.2f');
[x_r1,cdf_r1] = funcCDF(CNT_pnts, 0, deadline_N500r1, PntVal_N500Tau100r1);
plot(x_r1, cdf_r1, 'ob')
hold on
PntVal_N500Tau100r3 = textread('N500Tau100r3.tr','%*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %.2f');
[x_r3,cdf_r3] = funcCDF(CNT_pnts, 0, deadline_N500r3, PntVal_N500Tau100r3);
plot(x_r3, cdf_r3, 'or')
hold on
PntVal_N500Tau100r5 = textread('N500Tau100r5.tr','%*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %*s %.2f');
[x_r5,cdf_r5] = funcCDF(CNT_pnts, 0, deadline_N500r5, PntVal_N500Tau100r5);
plot(x_r5, cdf_r5, 'oc')
grid% --------------------- 3 效果图:
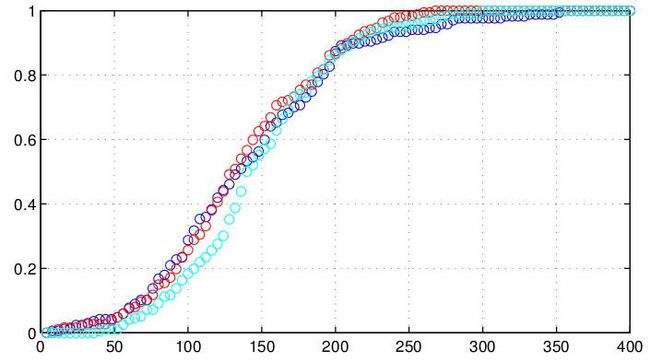
Fig.1 CDF_N200r3--Tau-60-80-100-100Pnts
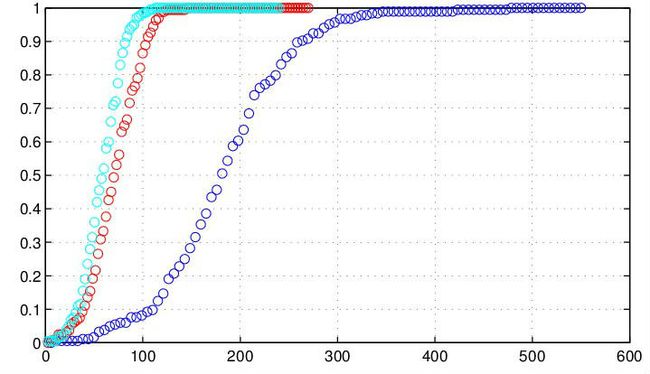
Fig.2 CDF_N500Tau100--r-1-3-5-100Pnts
当把参数 CNT_pnts = 100; 调为 CNT_pnts = 50; 后,显示在图中的点就会减少一半,shows as follow:
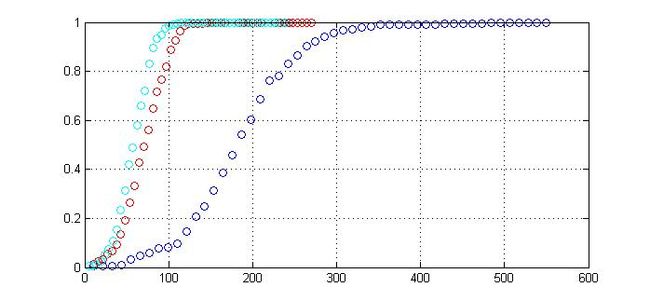
Fig.3 CDF_N500Tau100--r-1-3-5-50Pnts
Davy_H (2012-10-17)
============================================================================================
Section B. 第二种方法
今天(2014-10-15) 回过头来看这篇blog,前边贴的图太丑,而且其实第一种方法有不完美的地方,即数据少的时候,曲线有时不会从原点开始画。后来寻到更好的方法来画 CDF 图,为了对得起2000+的访问量,所以,今日我决定花些时间,把更好的例子分享出来。
废话不多说:1)效果图;2)部分数据文件;3)画图的脚本。
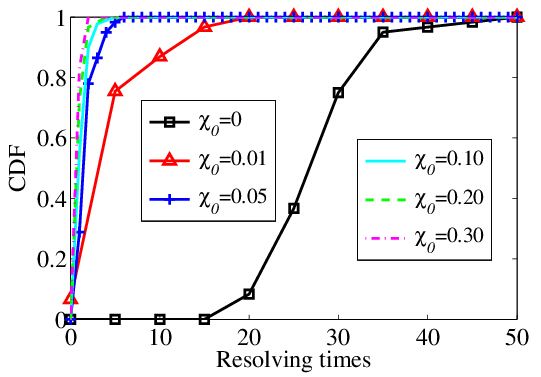
1) ------------------
2) ------------------ _Trace_file.tr
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 134 -C_FillUp 35 -Cost_OPT 77 -CNT_STimes 24 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 113 -C_FillUp 75 -Cost_OPT 43 -CNT_STimes 36 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 115 -C_FillUp 88 -Cost_OPT 26 -CNT_STimes 36 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 84 -C_FillUp 38 -Cost_OPT 44 -CNT_STimes 28 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 100 -C_FillUp 73 -Cost_OPT 35 -CNT_STimes 30 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 104 -C_FillUp 54 -Cost_OPT 38 -CNT_STimes 36 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 88 -C_FillUp 48 -Cost_OPT 41 -CNT_STimes 30 -Thresh 0
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 140 -C_FillUp 63 -Cost_OPT 80 -CNT_STimes 21 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 134 -C_FillUp 90 -Cost_OPT 55 -CNT_STimes 16 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 131 -C_FillUp 76 -Cost_OPT 62 -CNT_STimes 15 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 100 -C_FillUp 59 -Cost_OPT 53 -CNT_STimes 17 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 118 -C_FillUp 77 -Cost_OPT 46 -CNT_STimes 9 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 118 -C_FillUp 90 -Cost_OPT 67 -CNT_STimes 15 -Thresh 0.01
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 151 -C_FillUp 30 -Cost_OPT 123 -CNT_STimes 4 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 83 -C_FillUp 59 -Cost_OPT 20 -CNT_STimes 5 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 124 -C_FillUp 105 -Cost_OPT 2 -CNT_STimes 5 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 140 -C_FillUp 88 -Cost_OPT 91 -CNT_STimes 4 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 107 -C_FillUp 88 -Cost_OPT 17 -CNT_STimes 3 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 177 -C_FillUp 77 -Cost_OPT 77 -CNT_STimes 2 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 133 -C_FillUp 90 -Cost_OPT 27 -CNT_STimes 2 -Thresh 0.05
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 140 -C_FillUp 110 -Cost_OPT 32 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 115 -C_FillUp 97 -Cost_OPT 33 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 130 -C_FillUp 96 -Cost_OPT 46 -CNT_STimes 2 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 148 -C_FillUp 109 -Cost_OPT 66 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 144 -C_FillUp 105 -Cost_OPT 48 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 137 -C_FillUp 96 -Cost_OPT 58 -CNT_STimes 2 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 116 -C_FillUp 91 -Cost_OPT 52 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 117 -C_FillUp 97 -Cost_OPT 31 -CNT_STimes 1 -Thresh 0.1
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 149 -C_FillUp 96 -Cost_OPT 48 -CNT_STimes 3 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 127 -C_FillUp 106 -Cost_OPT 32 -CNT_STimes 2 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 108 -C_FillUp 87 -Cost_OPT 36 -CNT_STimes 2 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 134 -C_FillUp 105 -Cost_OPT 25 -CNT_STimes 2 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 140 -C_FillUp 79 -Cost_OPT 37 -CNT_STimes 1 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 158 -C_FillUp 107 -Cost_OPT 48 -CNT_STimes 2 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 142 -C_FillUp 99 -Cost_OPT 37 -CNT_STimes 1 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 114 -C_FillUp 92 -Cost_OPT 41 -CNT_STimes 1 -Thresh 0.2
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 158 -C_FillUp 64 -Cost_OPT 103 -CNT_STimes 2 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 151 -C_FillUp 108 -Cost_OPT 45 -CNT_STimes 1 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 115 -C_FillUp 74 -Cost_OPT 43 -CNT_STimes 2 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 147 -C_FillUp 110 -Cost_OPT 47 -CNT_STimes 1 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 154 -C_FillUp 67 -Cost_OPT 114 -CNT_STimes 2 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 152 -C_FillUp 92 -Cost_OPT 68 -CNT_STimes 1 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 132 -C_FillUp 74 -Cost_OPT 42 -CNT_STimes 2 -Thresh 0.3
-T 60 -K 10 -N_HC 30 -N_S 30 -C_DFLOWA 111 -C_FillUp 83 -Cost_OPT 29 -CNT_STimes 1 -Thresh 0.33) ------------------ Codes:
clear;
% --------------- A. Read the Data.
X_ = textread('_Trace_file.tr','%*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%f');
CNT_resolve_times = textread('_Trace_file.tr','%*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%*s %*s%d %*s%*s' );
% --------------- B. Count the the Costs.
% --------- X_items is the "-Threshold"
X_items =[0.0,0.01,0.05,0.1,0.2,0.3];
CNT_X = length(X_items);
% --------- Define the range_x of the x_coordinate in the figure.
step = 1;
range_end = 50;
range_x = 0:step:range_end;
figure
% ---------- Format of figure:
TextFontSize=18;
LegendFontSize = 16;
set(0,'DefaultAxesFontName','Times',...
'DefaultLineLineWidth',2,...
'DefaultLineMarkerSize',8);
set(gca,'FontName','Times New Roman','FontSize',TextFontSize);
set(gcf,'Units','inches','Position',[0 0 6.0 4.0]);
% ---------- Format of figure:~
% ------ Plot lines
for i = 1:1:CNT_X
Val_item = X_items(i);
idx_it_Lazy = find( X_ == Val_item );
% --- 1 CNT_STimes
CNT_Re_times_its = [];
CNT_Re_times_its = CNT_resolve_times( idx_it_Lazy );
% --- 2 Plot CDF of CNT_Resloving_times, i.e., the "CNT_STimes" in the trace file.
if (i==1) linePoint_type = '-sk'; step = 5; range_x = 0:step:range_end;
elseif (i==2) linePoint_type = '-^r';
elseif (i==3) linePoint_type = '-+b'; step = 1; range_x = 0:step:range_end;
elseif (i==4) linePoint_type = '-c'; step = 1; range_x = 0:step:range_end;
elseif (i==5) linePoint_type = '--g'; step = 1; range_x = 0:step:range_end;
elseif (i==6) linePoint_type = '-.m'; step = 1; range_x = 0:step:range_end;
end
%%% ====== Critical Code of CDF-Ploting :
h_rtl = hist( CNT_Re_times_its, range_x );
pr_approx_cdf = cumsum(h_rtl) / ( sum(h_rtl) );
%%% ====== Critical Code of CDF-Ploting :~
handler = plot( range_x, pr_approx_cdf, linePoint_type );
if (i==4) h4 = handler;
elseif (i==5) h5 = handler;
elseif (i==6) h6 = handler;
end
hold on
end
% --------- Set the other formats of the figure :
grid off
axis([0 range_end 0 1.0])
ylabel('CDF')
xlabel('Resolving times')
% --------- Plot the multi-legends :
hg1=legend('{\it \chi_0}=0', '{\it \chi_0}=0.01', '{\it \chi_0}=0.05', 0);
set(hg1,'FontSize',LegendFontSize);
ah1 = axes('position',get(gca,'position'), 'visible','off');
hg2 = legend(ah1, [h4,h5,h6], '{\it \chi_0}=0.10','{\it \chi_0}=0.20','{\it \chi_0}=0.30', 0);
set(hg2,'FontSize',LegendFontSize);
% --------- Plot the multi-legends :~
% --------- Set the other formats of the figure :~关键代码处,我已经做了注释,此处再强调一下:
1. 画 CDF 的2句关键代码,其中的3个 functions 请自己查询。
%%% ====== Critical operation of CDF-Ploting :
h_rtl = hist ( CNT_Re_times_its, range_x );
pr_approx_cdf = cumsum(h_rtl) / ( sum(h_rtl) );
%%% ====== Critical operation of CDF-Ploting :~
2. for 循环中的那一段 if else 语句,是为了设置各条曲线的点线型( linePoint type ) 与 各条线上的取样点的密度。
3. 此外,从这个脚本里,也可以额外获取 画多个图例 (plot multiple legends) 的方法。Davy_H (2014-10-15)
============================================================================================