环形链表专题
最近在刷LeetCode的题,对环形链表方面的题做个总结
文章目录
- 一、判断链表是否带环
- 1. 题目详情
- 2. 题目解析
- 解法一:快慢指针
- 解法二:哈希表/map
- 解法三: 非常规做法
- 二、带环链表入口
- 1. 题目详情
- 2. 题目解析
- 解法一:快慢指针
- 解法二:非常规做法
一、判断链表是否带环
1. 题目详情
环形链表-力扣(LeetCode)
2. 题目解析
解法一:快慢指针
我们定义两个指针,初始位置都放在头节点的地方,然后快慢指针一起走,快指针一次走两步(需要注意边界条件),慢指针一次走一步,如果快指针走到nullptr,该链表就不带环;如果快慢指针相遇,该链表就带环。
为什么这个办法可以解决,我们是需要给出理论依据的,先举个最常见的例子,两个人在操场跑步,一个人的速度是另一个人的两倍,如果跑的快的人追上跑的慢的人,那么快的人必然超过慢的人一圈。那么在链表中,也是一样的: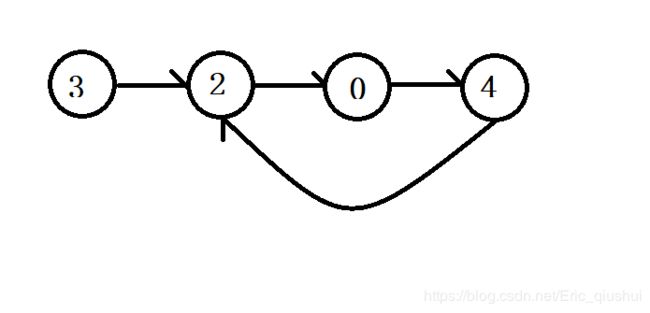
如果使用快慢指针,他们会在4的位置相遇,此时就可以返回了。
我们给出代码:
// 快慢指针
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head)
{
return false;
}
ListNode* fast = head;
ListNode* slow = head;
do
{
if(!fast || !fast->next)
return false;
slow = slow->next;
fast = fast->next->next;
}while(slow != fast);
return true;
}
};
复杂度分析:
- 时间复杂度:
O(n),n表示链表节点的个数- 链表不带环:快指针先到达链表结尾,其时间取决于链表的长度,时间复杂度
O(n) - 链表带环:我们将链表分为两个部分,非环部分和环形部分
- 慢指针在走完非环部分阶段后将进入环形部分:此时,快指针已经进入环中 迭代次数=非环部分长度 = N
- 两个指针都在环形区域中:考虑两个在环形赛道上的运动员 - 快跑者每次移动两步而慢跑者每次只移动一步。其速度的差值为1,因此需要经过 (两者之间距离)/(速度差值)次循环后,快跑者可以追上慢跑者。这个距离几乎就是 “环形部分长度 K” 且速度差值为 1,我们得出这样的结论 迭代次数=近似于 “环形部分长度 K”.
- 因此,在最糟糕的情况下,时间复杂度为
O(N+K), 也就是O(n)
- 空间复杂度
O(1)
- 链表不带环:快指针先到达链表结尾,其时间取决于链表的长度,时间复杂度
解法二:哈希表/map
我们遍历所有结点并在map中存储每个结点的引用(或内存地址)。如果当前结点为空结点 nullptr(即已检测到链表尾部的下一个结点),那么我们已经遍历完整个链表,并且该链表不是环形链表。如果当前结点的引用已经存在于map中,那么返回 true(即该链表为环形链表)。
// map
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head)
{
return false;
}
map key;
ListNode* pcur = head;
while(pcur)
{
if(key.find(pcur) != key.end())
{
return true;
}
else
{
++key[pcur];
}
pcur = pcur->next;
}
return false;
}
};
复杂度分析:
- 时间复杂度:底层基于红黑树的
map,在查找某个元素的时候,采用二分查找的办法,时间为O(lgn);链表n个节点,时间复杂度O(nlgn)。 - 空间复杂度:
O(n)
map可以解决,unordered_map当然也可以解决
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head)
{
return false;
}
unordered_map key;
ListNode* pcur = head;
while(pcur)
{
if(key.find(pcur) != key.end())
{
return true;
}
else
{
++key[pcur];
}
pcur = pcur->next;
}
return false;
}
};
至于set和unordered_set,自己试试就知道了。
复杂度分析:
- 时间复杂度:对于底层基于哈希表的
unordered_map,添加节点/查找节点的复杂度为O(1),遍历链表的n个元素需要时间O(n) - 空间复杂度:因为需要存储n个节点,空间复杂度
O(n)
解法三: 非常规做法
在浏览该题评论区的时候,发现一个骚操作:
堆地址从低到高,LeetCode的链表内存是顺序申请的,如果有环,
head->next一定小于head
附上代码:
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head)
{
return false;
}
ListNode* pcur = head;
while(pcur && pcur->next)
{
if(!less()(pcur, pcur->next))
{
return true;
}
pcur = pcur->next;
}
return false;
}
};
二、带环链表入口
1. 题目详情
环形链表II-力扣(LeetCode)
2. 题目解析
解法一:快慢指针
上一道题目,已经详细讲解了快慢指针判断链表带环,其实我们可以利用快慢指针相遇的节点,我们需要发觉一下这个点的魅力。
我们把节点增多几个,节点太少不好观察:

我们假设链表头结点到环入口位置距离为a,环的入口与相遇节点位置距离为b,环的长度为R,我们计算快慢指针所走过的距离:
d(fast) = a + b + n * R
d(slow) = a + b
快指针的速度是慢指针的两倍,相同时间,快指针所走过的路程应该是慢指针所走过路程的两倍,于是:
d(fast) = 2 * d(slow)
所以有:a = n * R - b
当n = 1时,也就是快指针走了一圈之后,在第二圈的时候遇见了慢指针,a = R - b
我们可以发现,a是链表的表头到环的入口点的位置,(R - b)是相遇点到环入口点的位置。
但是我们需要考虑一种特殊情况,链表是首尾相连的:

我们可以发现,如果链表的表头就是入口点,使用快慢指针的时候,因为快指针是慢指针的速度的2倍,所以它们一定是慢指针走了一圈,快指针走了两圈的时候相遇,就是在环的入口点相遇。
附上代码:
class Solution
{
public:
ListNode *detectCycle(ListNode *head)
{
if(!head)
{
return nullptr;
}
ListNode *slowptr = head;
ListNode *fastptr = head;
/*
* 快慢指针
* 如果快指针追上慢指针,说明链表带环
* 并且快慢指针相遇的点一定是换上的一点
*/
do
{
if(fastptr == nullptr || fastptr -> next == nullptr)
return nullptr;
slowptr = slowptr -> next;
fastptr = fastptr -> next -> next;
}while(slowptr != fastptr);
/*
* 让慢指针回到头节点位置
* 然后快慢指针一起走
* 再次相遇的地方必然是环的入口
* 原因:
*/
slowptr = head;
while(slowptr != fastptr)
{
slowptr = slowptr -> next;
fastptr = fastptr -> next;
}
return slowptr;
}
};
解法二:非常规做法
堆的地址从低到高,LeetCode的链表内存是顺序申请的,如果有环,head->next一定小于head
class Solution {
public:
ListNode *detectCycle(ListNode *head)
{
while(head)
{
if(!less()(head, head->next))
{
return head->next;
}
head = head->next;
}
return nullptr;
}
};
如有问题,欢迎指正,谢谢:)