MATLAB神经网络编程（十）——Hopfield网络结构与应用

《MATLAB神经网络编程》 化学工业出版社 读书笔记
第六章反馈型神经网络 6.1 Hopfield网络

本文是《MATLAB神经网络编程》书籍的阅读笔记，其中涉及的源码、公式、原理都来自此书，若有不理解之处请参阅原书

---

---

6.1.4 Hopfield网络结构

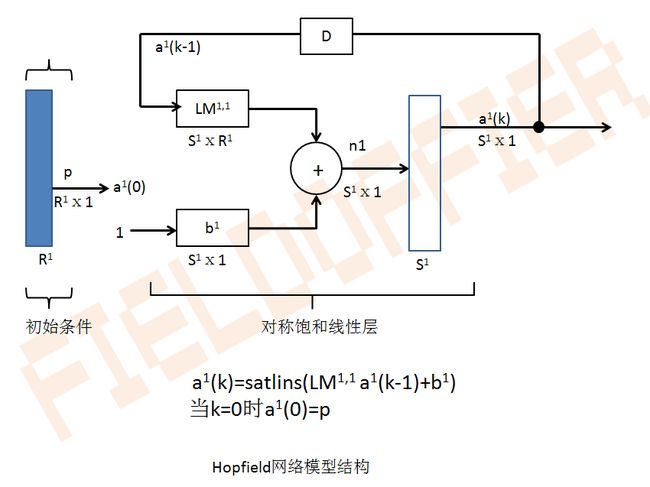
在MATLAB神经网络工具箱中，Hopfield网络为单层网络模型，其结构如下图：

输入p是Hopfield网络的初始条件，其隐层神经元为饱和线性传递函数satlins，如下图：

6.1.5 Hopfield网络模型学习过程

网络的学习过程实际上就是权值调整过程，Hopfield网络的学习目的就是调整连接权值，以使得网络的稳定平衡状态就是所要求的状态。
Hopfield网络常常采用的学习算法是Hebb学习规则，即权值调整规则为：若第i和第j个神经元同时处于兴奋状态，那么他们之间的连接应该增强，权值应该增大。如下所示：

newhop函数是设计Hopfield网络的一种方法。给出一系列平衡期望值矩阵T，newhop函数的输出是反馈网络的权值和阈值，之前需要保证网络对应期望值向量具有稳定的平衡点，但是通常会存在一些伪平衡点，设计方法是使伪平衡点数量越少越好。

newhop( )
功能 生成一个Hopfield回归网络。
格式 net = newhop(T)
说明 net为生成的神经网络，具有在T中的向量上稳定的点；T是具有Q个目标向量的R*Q矩阵（元素必须为-1或1）。Hopfield神经网络经常被应用于模式的联想记忆中。Hopfield神经网络仅有一层，其激活函数用satlins( )函数，层中的神经元有来自它自身的连接权和阈值。
注意：T是R*Q矩阵，表明生成的Hopfield网络有Q个稳定点，即T的列向量表示的点就是稳定点。关于这一点的具体含义可以参下面的例子。

6.1.6 几个重要的结论

1，联想记忆功能：由于网络可以收敛于稳定状态，因此可以用于联想记忆。若将稳态视为一个记忆，则由初始状态向稳态收敛的过程就是寻找记忆的过程，初始状态可认为是给定的部分信息，收敛过程可以认为是从部分信息找到了全部信息，则实现了联想记忆功能。(联想记忆是Hopfield及其重要的特征)
2，优化计算：若将稳态视为某一优化问题目标函数的极小点，则由初始状态向稳态收敛的过程就是优化计算过程。
3，网络渐进稳定的前提是Wij=Wji
4,网络的应用：Hopfield网络多用于在控制系统的设计中求解约束优化问题，另外在系统辨识中也有应用。

6.1.7 Hopfield网络的应用

【例6-2】设计一个三维空间中有两个稳定平衡点的网络，期望值向量为T。
分析：两个平衡点，说明矩阵T有两列，三维空间，表明每一个点需要三个分量表示，所以T的每一列有三个分量；故T是3*2的矩阵。

源码：

%T是网络的稳定点，由于没有输入，所以T也是Hopfield网络的输入
T=[-1 -1 1;1 -1 1]'
%构建一个Hopfield网络
net=newhop(T);

Ai=T;
[Y,Pf,Af]=sim(net,2,[],Ai);
Y

执行结果：

可见网络设计确实能够做到设计点稳定。

关于sim函数的参数含义：
doc里面查找到的帮助
sim simulates neural networks.
[Y,Pf,Af,E,perf] = sim(net,P,Pi,Ai,T) takes
net
Network
P
Network inputs
Pi
Initial input delay conditions (default = zeros)
Ai
Initial layer delay conditions (default = zeros)
T
Network targets (default = zeros)
and returns
Y
Network outputs
Pf
Final input delay conditions
Af
Final layer delay conditions
E
Network errors
perf
Network performance

Each matrix argument is found by storing the elements of
the corresponding cell array argument into a single matrix:
P - (sum of Ri)xQ matrix
Pi - (sum of Ri)x(ID*Q) matrix.
Ai - (sum of Si)x(LD*Q) matrix.
T - (sum of Vi)xQ matrix
Y - (sum of Ui)xQ matrix.
Xf - (sum of Ri)x(ID*Q) matrix.
Af - (sum of Si)x(LD*Q) matrix.
E - (sum of Vi)xQ matrix

[Y,Pf,Af] = SIM(net,{Q TS},Pi,Ai) is used for networks
which do not have an input, such as Hopfield networks
when cell array notation is used.

下面输入不同于设计点的其他初始值再来检验一下：

%下面输入不同于设计点的其他初始值再来检验一下
Ai={[-0.9;-0.8;0.7]};
[Y,Pf,Af]=sim(net,{1,5},{},Ai);
Y
%Y{1}
Y{3}

输出：

上面代码中输入是[-0.9;-0.8;0.7]，输出变成了稳点点[-1;-1;1]，这是因为Hopfield网络已经收敛，所以网络的输出只能是稳定点，本例中稳点只有两个，所以输出是与输入最接近的那一个点

---

【例6-3】含有两个神经元的Hopfield网络的设计。

PS：Hopfield网络是单层的，即隐层只有一层；含有两个神经元即指隐层有两个神经元；此时目标向量T的每一列都有两个分量，即T有两行；

网络所要存储的目标平衡点是一个列矢量T：T=[1,-1;-1,1];在二维平面内绘制出这两个稳定平衡点，如下图：

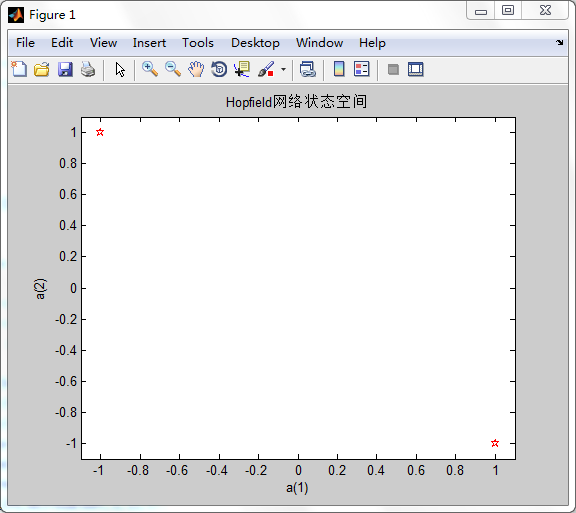
原则上所设计的Hopfield网络的所以可能状态都应包含在图上的区间内，所以称为Hopfield 网络状态空间。

 T=[1 -1; -1 1]
plot(T(1,:),T(2,:),'rp');
axis([-1.1 1.1 -1.1 1.1]);
title('Hopfield网络状态空间');
xlabel('a(1)');ylabel('a(2)');
 net=newhop(T);
 [Y,Pf,Af]=sim(net,2,[],T);
 Y

程序输出如下：

Y =
1 -1
-1 1

可见，网络输出能够稳定到期望值。
再随机选取初始点，然后应用sim函数进行仿真，其结果应该稳定到两个平衡点之一：

a={rands(2,1)};

%a这里作为输入，下面的格式与sim函数的格式有些不同，是为无输入网络的格式
[y,Pf,Af]=sim(net,{1 20},{},a);

 record=[cell2mat(a) cell2mat(y)];
start=cell2mat(a);
hold on;
plot(start(1,1),start(2,1),'bx',record(1,:),record(2,:))

执行结果：

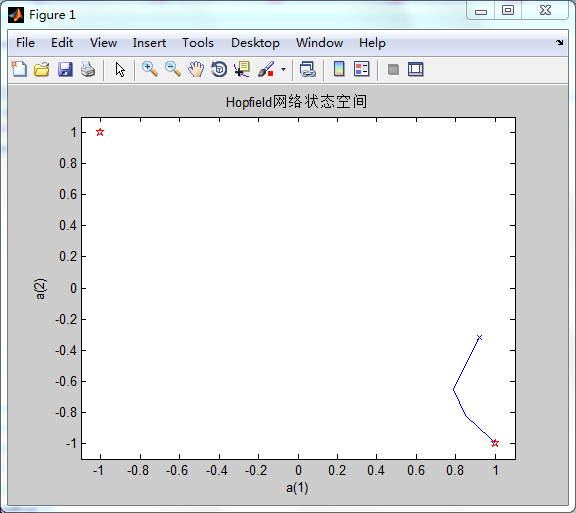
注意，根据随机矩阵a的不同会有不同的结果，但是每一个结果都会稳定到左上角或者右下角的稳定点上。
比如，随机选择25个初始点进行测试：

 color='rgbmy';
for i=1:25
    a={rands(2,1)};
    [y,Pf,Af]=sim(net,{1 20},{},a);
    record=[cell2mat(a) cell2mat(y)];
    start=cell2mat(a);
    plot(start(1,1),start(2,1),'kx',record(1,:),record(2,:),color(rem(i,5)+1));
end

执行结果：

从上图可以看出，所有的点最后都收敛于两个平衡点与左上角接近的点收敛于左上角，与右下角接近的点收敛于右下角。由此可见，Hopfield网络具有联想记忆功能。

---

【例6-4】含有三个神经元的Hopfield网络的设计。

PS：Hopfield网络是单层的，即隐层只有一层；含有三个神经元即指隐层有三个神经元；此时目标向量T的每一列都有三个分量，即T是三行；

本例设计一个由三个神经元的Hopfield网络并进行仿真验证，它具有两个稳定的平衡点。（即T有两列）
要求设计一个Hopfield网络，其期望矩阵是T：T=[1 1;-1 1;-1 -1];在三维空间绘制出这两个平衡点。
源码：

T=[1 1;-1 1;-1 -1];
axis([-1 1 -1 1 -1 1]);
set(gca,'box','on');
axis manual; hold on;
plot3(T(1,:),T(2,:),T(3,:),'rp');
title('含三个神经元的Hopfield网络状态空间');
xlabel('a(1)'); ylabel('a(2)');
zlabel('a(3)'); view([-36 30]);

设计Hopfield网络，随机选取初始点，应用sim函数进行仿真，其结果应该是稳定到两个平衡点之一：

%建立Hopfield网络，以满足期望值T的要求
net=newhop(T);

 a={rands(3,1)};
[y,Pf,Af]=sim(net,{1,10},{},a);
 record=[cell2mat(a) cell2mat(y)];
start=cell2mat(a);
hold on;
plot3(start(1,1),start(2,1),start(3,1),'bx',...
    record(1,:),record(2,:),record(3,:));
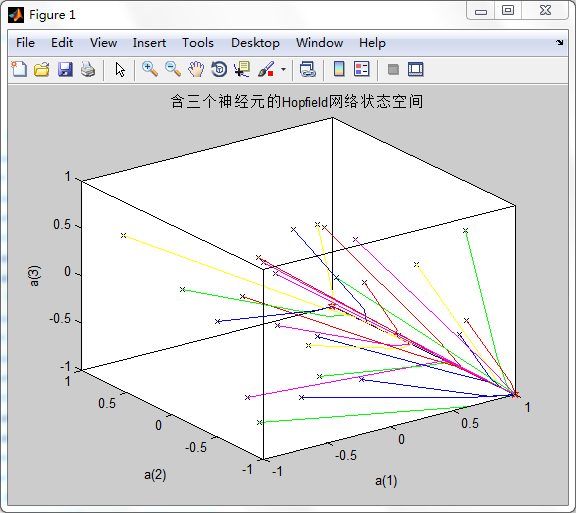
color='rgbmy';
for i=1:25
    a={rands(3,1)};
    [y,Pf,Af]=sim(net,{1 10},{},a);
    record=[cell2mat(a) cell2mat(y)];
    start=cell2mat(a);
    plot3(start(1,1),start(2,1),start(3,1),'kx',record(1,:),...
        record(2,:),record(3,:),color(rem(i,5)+1));
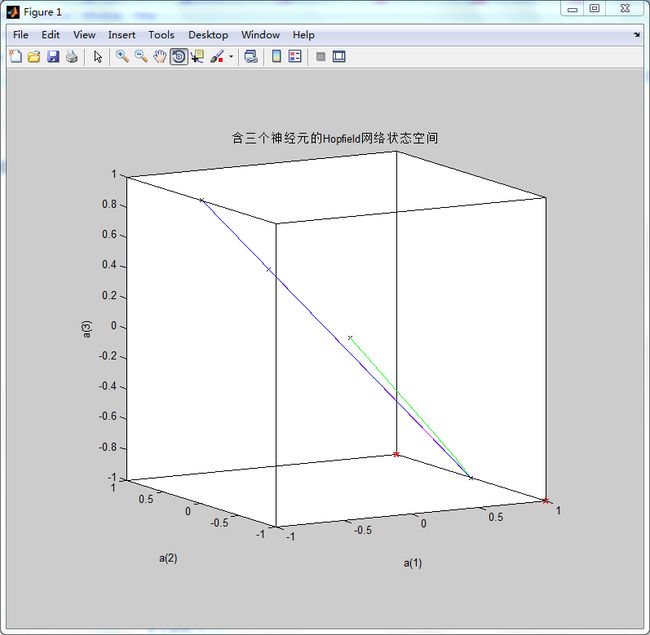
end

结果：

然后是比较有意思的情况，选取一些恰恰位于两个平衡点正中的位置上，然后绘制出这些点的走向：

%p是三行六列，表明有6个输入点
 P=[1.0 -1.0 -0.5 1.0 1.0 0.1;0.0 0.0 0.0 0.0 0.0 -0.0;-1.0 1.0 0.5 -1.0 -1.0 0.0];
cla
plot3(T(1,:),T(2,:),T(3,:),'rp');
clor='rgbmy';
for i=1:6
    a={P(:,i)};
    [y,Pf,Af]=sim(net,{1 10},{},a);
    record=[cell2mat(a),cell2mat(y)];
    start=cell2mat(a);
    plot3(start(1,1),start(2,1),start(3,1),'kx',record(1,:),...
        record(2,:),record(3,:),color(rem(i,5)+1));
end

程序结果：

从上图中可以看出，6个初始点最后都移动到了状态空间中心点位置，而这个点不是网络设计所设定的平衡点。此时，这个中心点就是设计中不希望出现的伪平衡点。

---

【例6-5】设计一个Hopfield网络，使其具有联想记忆功能，能正确识别阿拉伯数字，当数字被噪声污染后仍可以正确识别。
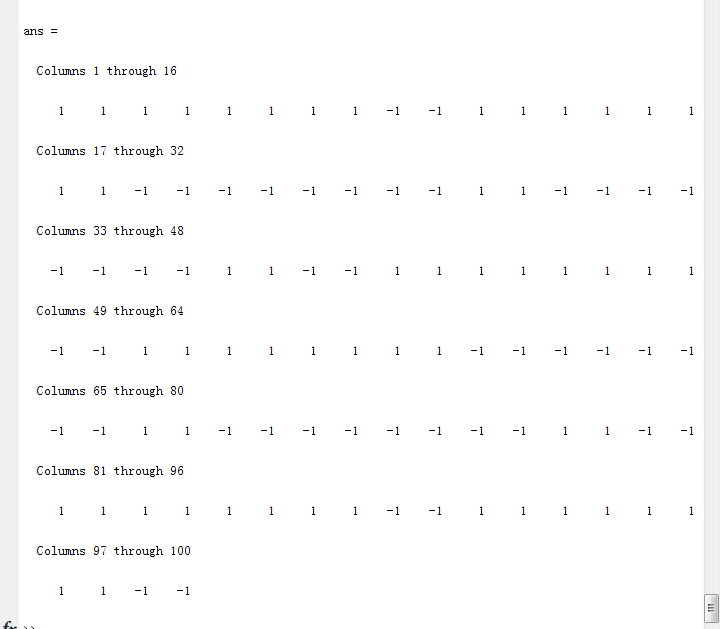
假设网络由10个初始稳态值0~9构成，即可以记忆10种数字。每个稳态由10*10的矩阵构成，该矩阵用于模拟阿拉伯数字点阵。这里把数字划分成一个10*10方阵，其中有数字的方块用1表示，空白用-1表示，如下图：

%数字1的点阵表示

one=[-1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1  -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1];

%数字2的点阵表示

two=[1 1 1 1 1 1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1];

%这里只列出1和2的点阵表示。利用这两个向量构成一个训练样本，由此构建一个Hopfield网络。

%设定网络的目标向量

T=[one;two]';

%创建一个Hopfield神经网络

net=newhop(T);

%给定一个受噪声污染的数字2的点阵，所谓噪声是指数字点阵中某些本应为1的方块变成了-1

no2={[1 1 1 -1 1 1 -1 1 -1 -1  1 1 1 1 1 1 1 1 -1 -1  -1 1 -1 1 -1 -1 1 1 -1 -1 -1 -1 1 -1 1 -1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1 1 1 1 1 1 1 1 1 -1 -1  1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 -1 1 1 1 1 -1 -1 1 1 -1 1 1 1 1 1 -1 -1]'};

%对网络进行仿真，网络的仿真步数为5

tu2 =sim(net,{1,5},{},no2)

%输出仿真结果向量矩阵中的第3列向量，并将其转置

tu2{3}’   %输出由新的输入产生的结果

输出结果：

结果和数字2的正常点阵是一致的，说明网络从受到污染的数字2的点阵中识别出了数字2，此网络是有效的。

---

【例6-6】演示Hopfield网络出现伪平衡点的情况。
假定需要设计一个Hopfield网络，具有两个稳定平衡点，其期望向量T如下：T=[1 -1;-1 1];在二维平面内绘制这两个稳定平衡点：

T=[1 -1;-1 1];
 plot(T(1,:),T(2,:),'rp');
axis([-1.1 1.1 -1.1 1.1]);
title('Hopfield网络状态空间');
xlabel('a(1)'); ylabel('a(2)');

%设计一个Hopfield网络，满足期望值T的要求
net=newhop(T);
 W=net.LW{1,1} %权值
 b=net.b{1,1} %阈值

结果如下：

W =

    0.6925   -0.4694
   -0.4694    0.6925


b =

  1.0e-015 *

   -0.0316
   -0.1754

注意上面结果中其实b=[0;0]

 Ai=T;%应用期望值作为输入，在用sim函数进行检测
[Y,Pf,Af]=sim(net,2,[],Ai);
Y

输出结果：

Y =

     1    -1
    -1     1

可见，网络输出能够稳定到期望值。
然后随机选取初始点，并用sim函数进行仿真，其结果应该稳定到两个平衡点之一：

a={rands(2,1)};
[y,Pf,Af]=sim(net,{1,50},{},a);
record=[cell2mat(a) cell2mat(y)];
start=cell2mat(a);
hold on;
plot(start(1,1),start(2,1),'bx',record(1,:),record(2,:));

程序结果：

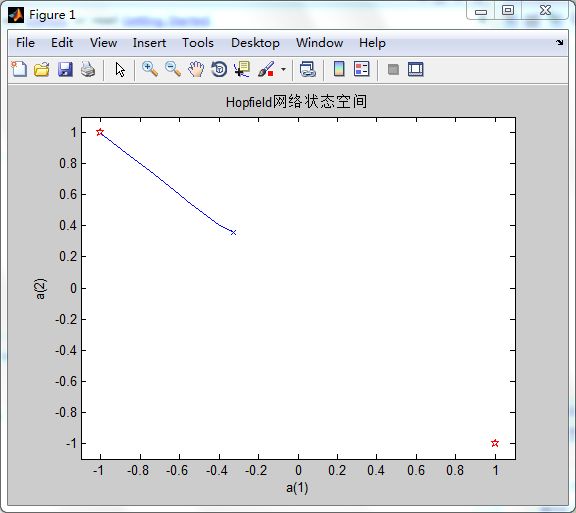
可见，随机选取的初始点最后稳定在左上角的平衡点；（当然，根据a随机到的不同值，也有可能是稳定在右下角）

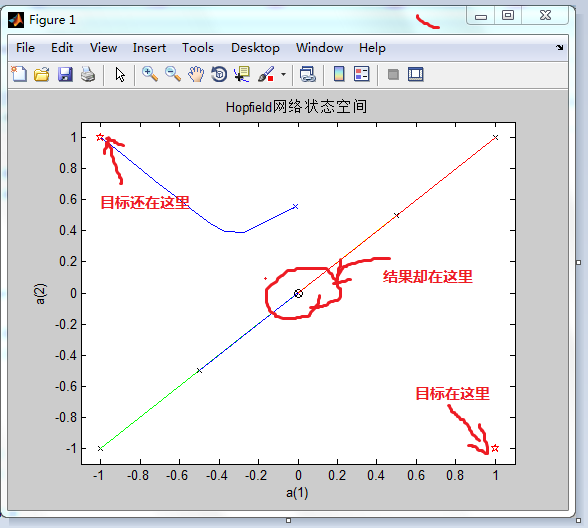
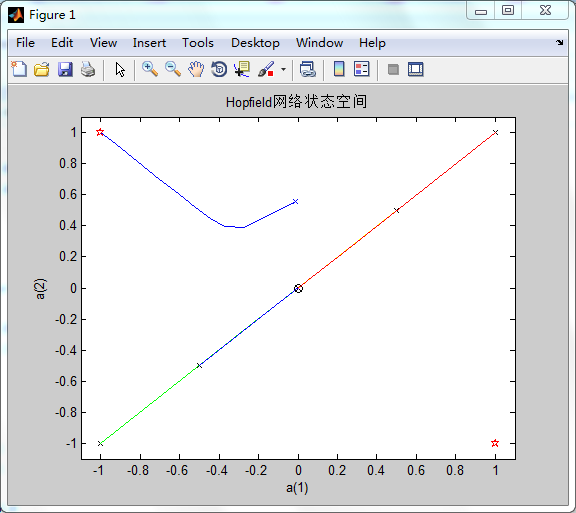
下面选取5个初始点来说明伪平衡点的情况，5个点在向量空间恰好位于两个期望稳定点正中的位置上：

plot(0,0,'ko');
P=[-1.0 -0.5 0.0 0.5 1.0;-1.0 -0.5 0.0 0.5 1.0];
color='rgbmy';
for i=1:5
    a={P(:,i)};
    [y,Pf,Af]=sim(net,{1 50},{},a);
    record=[cell2mat(a) cell2mat(y)];
    start=cell2mat(a);
    plot(start(1,1),start(2,1),'kx',...
        record(1,:),record(2,:),color(rem(i,5)+1));
end

结果：

从图上看出，5个初始点最后都移动到了状态空间中心的位置，而这个点不是网络设计之前设定的平衡点。此时状态空间中心点就是网络设计中不期望出现的伪平衡点。