扫描线算法讲解+例题
会遇到这种题:给你很多矩形,如果一个区域被多次覆盖,只计算一次,问总面积.
一直说是线段树,但是不知道是扫描线,写篇博客记录一下.
扫描线是这么个意思
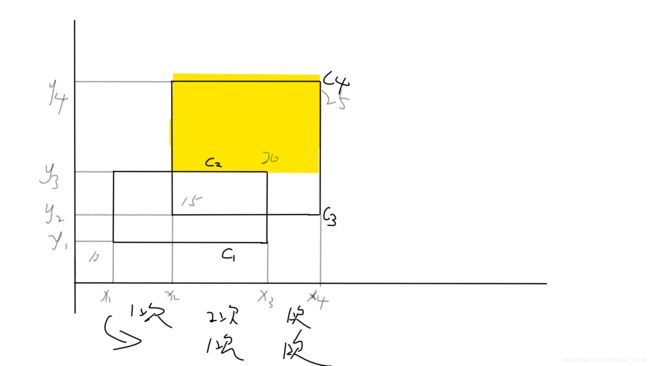
肯定需要离散化了,可以选择离散化x轴或者y轴的点,然后就分割成了几个区间,x1到x2,x2到x3,x3到x4,我们以xi代表以它为起点,以下一个离散化的点为终点的线段.
然后我们有四个高度,y1,y2,y3,y4,可以知道,面积等于(y2-y1)*(x3-x1)+.........这样面积实际上就可控了.
那么具体操作怎么办捏,以离散化x轴为栗子,我们在输入的时候可以找到一个上边和下边,我们把下边标记为1,上边标记-1,
排序之后,y1,2,3,4顺次排序,
现在开始处理:
这是第一次的情况,y1是下底边,[x1,x3)被标记为1,然后乘以这段的高.以HDU1542的样例为假设,
样例:
2
10 10 20 20
15 15 25 25.5
0则黄色部分就是(20-10)*(15-10) = 50;
第二次的情况:
现在我们扫描了y2,此时我们的对x2,x3进行了扫描,现在横轴长度变为[x1,x4),为什么捏,因为之前的图一,黄色部分覆盖了[x1,x3),现在[x2,x3)被扫描两次,[x1,x2)被扫描一次,所以,此时的面积是蓝色部分加上和蓝色部分平行的黄色部分,是(20-15(高))*(25-10(长)) = 75.
第三次扫描,是对y3进行扫描,之前都是下边界,现在遇到上边界-1的情况了.
下面的箭头就是这个上边界扫描完产生的变化,然后面积就是黄色部分加起来,再之后是y4的扫描,-1之后等于0,可扫可不扫.
//Atlantis HDU - 1542
#include
using namespace std;
const int maxn = 505;
int lazy[maxn<<2];
int add[maxn<<2];
double x[maxn<<2],sum[maxn<<2];
struct EDGE
{
int ss;//上下边
double l,r,h;//左右,高度
EDGE(double _x1=0,double _x2=0,double _y=0,int _up_or_down=0)
{
l = _x1;
r = _x2;
h = _y;
ss = _up_or_down;
}
bool operator<(const EDGE & a)
{
return h= r)
{
add[rt] += val;
pushUP(rt,l,r);
return;
}
mid = (l+r)>>1;
if(L<=mid)
update(rt<<1,L,R,val,l,mid);
if(R>mid)
update(rt<<1|1,L,R,val,mid+1,r);
pushUP(rt,l,r);
}
int main()
{
// freopen("in.txt","r",stdin);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n;
int kase = 1;
double x1,y1,x2,y2,ans;
while(cin>>n && n)
{
ans = 0;
int top = 0,l,r;
printf("Test case #%d\n",kase++);
printf("Total explored area: ");
for(int i=0; i>x1>>y1>>x2>>y2;
x[top] = x1;
dian[top++] = EDGE(x1,x2,y1,1);//下边界标记为1
x[top] = x2;
dian[top++] = EDGE(x1,x2,y2,-1);//上边界标记为-1
}
sort(x,x+top);
sort(dian,dian+top);
int k = 1;
for(int i=1; i 然后开始解析代码职能,sum需要统计的是add标记过的长度,add是标记现在当前段被几个下边界+1,我们的边需要按照高度从小到大排序,ss表示+1和-1,sum[1]就是被标记的有效长度,然后由于区间是[)的,所以r lower_bound之后需要-1,
关于去重:据说可去可不去,意义:把x轴离散化之后变成有序的,相当于打个映射.二分的时候直接是严格单调递增的,其他的没有影响.
变形题:
Rectangles Gym - 101982F
当时打死都不会,还以为是二维线段树,其实好像没这东西,全是自己瞎猜的.
现在要处理的问题比较狗了一点,还是那么扫描,但是负负得正,正正得负,记得一个运算,^运算,所以我们现在+val应该改成^1;
//【扫描线】Gym - 101982 - F - Rectangles
#include
using namespace std;
typedef long long LL;
const int maxn = 1e5+5;
int lazy[maxn<<3];
int add[maxn<<3];
int x[maxn<<2],sum[maxn<<3];
struct EDGE
{
int ss;//上下边
int l,r,h;//左右,高度
EDGE(int _x1=0,int _x2=0,int _y=0)
{
l = _x1;
r = _x2;
h = _y;
}
bool operator<(const EDGE & a)
{
return h>1;
cal(rt<<1,l,mid);//计算sum
cal(rt<<1|1,mid,r);
add[rt] = 0;
}
void update(int rt,int L,int R,int l,int r)//更新[L,R]区间
{
int mid;
if(L<=l && R >= r)//如果rt包含的区间完全被覆盖
{
add[rt] ^= 1;
cal(rt,l,r);
return;
}
pushDown(rt,l,r);//向下更新一次懒惰标记
mid = (l+r)>>1;
if(Lmid)
update(rt<<1|1,L,R,mid,r);
pushUP(rt);
}
int main()
{
int n;
scanf("%d",&n);
int x1,x2,y1,y2,all=0;
for(int i=1; i<=n; i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
e[2*i-1].l=min(x1,x2);//l严格小于r
e[2*i-1].r=max(x1,x2);
e[2*i-1].h=min(y1,y2);
e[2*i].l=min(x1,x2);
e[2*i].r=max(x1,x2);
e[2*i].h=max(y1,y2);
x[2*i-1]=x1,x[2*i]=x2;
}
sort(x+1,x+1+n*2);
all=unique(x+1,x+1+n*2)-x-1;
for(int i=1; i<=2*n; i++)//处理出来l和r在离散化之后的x轴上的区间
e[i].l=lower_bound(x+1,x+1+all,e[i].l)-x,e[i].r=lower_bound(x+1,x+1+all,e[i].r)-x;
sort(e+1,e+1+2*n);
LL ans=0;
for(int i=1; i<2*n; i++)
{
update(1,e[i].l,e[i].r,1,all);//更新这条线段
ans+=(LL)sum[1]*(e[i+1].h-e[i].h);
}
printf("%lld\n",ans);
}