Keras-Tutorial(三)
Keras-Tutorial(三)
在小数据集上使用K-fold validation为Regression Model寻找更好的超参数。
上两讲中,我们都是进行分类任务。
这一讲中,我们使用神经网络建立一个回归模型进行房价预测。
数据集介绍
这一讲中,使用的是Boston房价数据集,该数据集讲述的是1970的中期阶段的房价。
总共包含506个样本(404个训练样本,102个测试样本)。
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import boston_housing
from keras.models import Sequential
from keras.layers import Dense
# 导入数据集
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
# 查看数据集shape
print("The shape of train_data: ", train_data.shape)
print("The shape of train_targets: ", train_targets.shape)
print("The shape of test_data: ", test_data.shape)
print("The shape of test_targets: ", test_targets.shape)
# 从以上的shape中,可以看到,每个样本都是又13个特征组成的,例如犯罪率等这些特征。
# 而target则是一个值,一个连续值。
# 查看每个样本的值
print("The train_data[0]: ", train_data[0])
print("The train_targets[0]: ", train_targets[0])数据预处理
由于每个特征的量纲不同(即取值范围不同),例如,犯罪率(0.0-1.0),平均房间数量(>1)。
将不同量纲的特征一起input到同一个神经网络中进行训练,会使得训练变难,所以我们需要进行数据标准化(不了解标准化的,可以回头看看我之前写的特征工程系列)。
当然,你也可以选择不进行数据标准化,但这不是明智的选择。
# 获取平均值
mean = train_data.mean(axis=0)
print("The mean of features: ", mean)
train_data -= mean
# 获取标准差
std = train_data.std(axis=0)
print("The std of features:", std)
train_data /= std
# 当然,测试机也要进行同样的操作
test_data -= mean
test_data /= std建立模型
def bulid_network(optimizer='rmsprop', loss='mse', metrics='mae'):
# build
# 由于数据集的规模比较小,所以我们尽量使用比较浅的模型,比较深的模型对于小数据集来说容易过拟合
model = Sequential()
model.add(Dense(units=64, activation='relu', input_shape=(train_data.shape[1], )))
model.add(Dense(units=64, activation='relu',))
model.add(Dense(units=1))
# compile
# 这里使用mean square loss的loss function,因为这是个回归模型,而mse是回归模型中使用比较多的loss function
# 表示真实值与预测值的残差平方和
# metrics监控使用mean absolute error,平均绝对误差,和mse只是相差一个平方
model.compile(optimizer=optimizer, loss=loss, metrics=[metrics])
return modelK-fold cross validation
这里我们使用k-折叠交叉验证
* 由于我们的数据是一个小数据集,如果我们按照7:3的比例进行划分训练集和验证集,则验证机也只是几十个样本左右。
* 因为验证机的规模更小,很难全面包括整个数据集的真实分布,而模型的评价也要依靠验证集的评分,会造成很高的variance。
* 我们将训练集和划分为K份,然后进行1-k次的模型迭代,选择k-1份的作为训练集,剩余的为测试集,如图示:
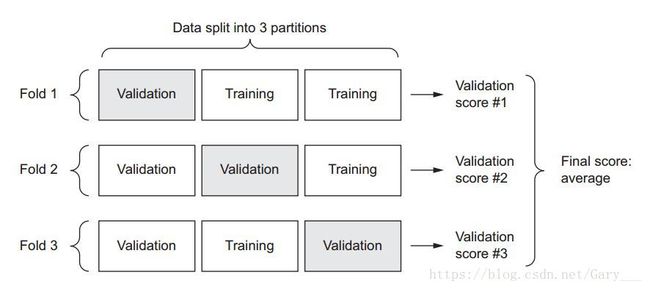
* 然后分数为每次的验证分数的平均值。
* 通过k次的交叉验证,可以很大的掌握数据集的分布。
# 我们使用numpy来进行划分
# 划为k份
k = 4
# val_set的的样本数目
num_val_samples = len(train_data) // k
epochs = 100
all_scores = [] # 用于保存k次validation的score
for i in range(k):
print('processing_fold #', i+1)
# 开始划分数据
val_data = train_data[i * num_val_samples : (i + 1) * num_val_samples]
val_tagets = train_targets[i * num_val_samples : (i + 1) * num_val_samples]
# 进行组合
partial_train_data = np.concatenate([train_data[0: i * num_val_samples ], train_data[( i + 1) * num_val_samples: ]], axis=0)
partial_train_targets = np.concatenate([train_targets[0: i * num_val_samples ], train_targets[( i + 1) * num_val_samples: ]], axis=0)
# 创建模型
model = bulid_network()
# verbose=0, 表示不输出训练信息
model.fit(partial_train_data, partial_train_targets, epochs=epochs, batch_size=16, verbose=0)
val_mse, val_mae = model.evaluate(val_data, val_tagets, verbose=0)
all_scores.append(val_mae)
# 查看分数
print('All scores: ', all_scores)
print('mean scores: ', np.mean(all_scores))
# All scores: [1.924640688565698, 2.4316208055703945, 2.514633008749178, 2.370800575407425]
# mean scores: 2.3104237695731737从结果中可以看到,每次的运行的分数都不一样(1.9-2.5),但平均分2.3看起来更加的可靠点。
保存验证集的训练日志
epochs = 500
all_mae_histogries = []
for i in range(k):
print('processing_fold #', i+1)
# 开始划分数据
val_data = train_data[i * num_val_samples : (i + 1) * num_val_samples]
val_tagets = train_targets[i * num_val_samples : (i + 1) * num_val_samples]
# 进行组合
partial_train_data = np.concatenate([train_data[0: i * num_val_samples ], train_data[( i + 1) * num_val_samples: ]], axis=0)
partial_train_targets = np.concatenate([train_targets[0: i * num_val_samples ], train_targets[( i + 1) * num_val_samples: ]], axis=0)
# 创建模型
model = bulid_network()
# verbose=0, 表示不输出训练信息
history = model.fit(partial_train_data, partial_train_targets, validation_data=(val_data, val_tagets),
epochs=epochs, batch_size=16, verbose=0)
# 记录
mae_history = history.history['val_mean_absolute_error']
all_mae_histogries.append(mae_history)
# 计算平均error,即每一个eoches,每个val_error的第epoches的平均值
average_mae_history = [np.mean([x[i] for x in all_mae_histogries]) for i in range(epochs)]将曲线绘制出来
plt.plot(range(1, epochs + 1), average_mae_history)
plt.title('The Average MAE logs\n')
plt.xlabel('Epoch #')
plt.ylabel('Validation MAE')
plt.legend()
plt.show()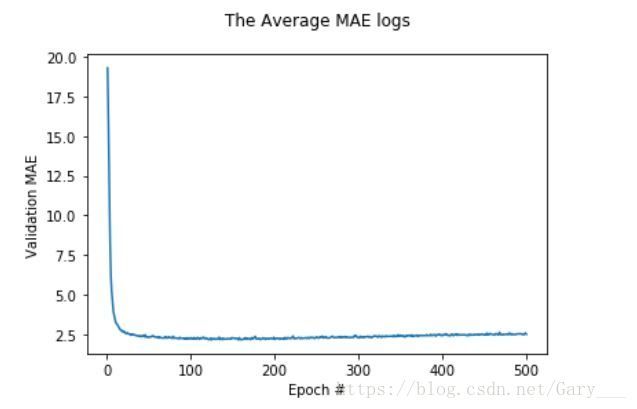
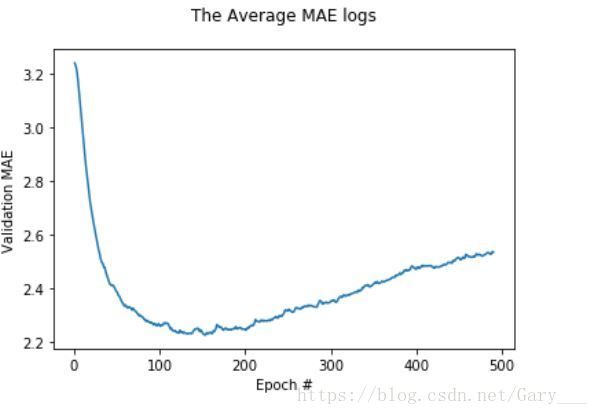
**但从以上这幅图,我们感觉应该是在epoch=120左右,模型就已经停止改善了,并且开始过拟合。
我们来证明这一点**
平滑数据
- 由上图中看出,前10个epoch的数据variance比较大,所以我们舍弃这10个点。
- 用剩余的点进行这样的操作:每个点替换为前面点的指数移动平均值,以获得平滑曲线。
- 那到底什么是指数移动平均(Exponential moving average, EMA, 它起到的效果是移动平均线能较好的反应时间序列的变化趋势,权重的大小不同起到的作用也是不同,时间比较久远的变量值的影响力相对较低,时间比较近的变量值的影响力相对较高*
- 这里不详细解释EMA,想更好地理解EMA,建议去看Andrew老师的Machine Learning课程哦*
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
# 已经存在数据,则用最后一个点的加权数据
if smoothed_points:
previous = smoothed_points[-1]
point = previous * factor + point * (1 - factor)
smoothed_points.append(point)
else:
# 第一个点
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.title('The Average MAE logs\n')
plt.xlabel('Epoch #')
plt.ylabel('Validation MAE')
plt.legend()
plt.show()# 重新训练
epochs = 120
model = bulid_network()
model.fit(partial_train_data, partial_train_targets,
epochs=epochs, batch_size=16, verbose=1)
# 评估模型
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
print('Test Mse score: ', test_mse_score)
print('Test Mae score: ', test_mae_score)当然,我们也可使用k-fold找到更多优秀的参数,如learning_rate, batch_size等超参数。
详细代码,请参考:https://github.com/Gary-Deeplearning/Keras-Tutorial