再谈数据结构(二)数和二叉树
1 - 引言
关于树和二叉树,我们需要达到的能力有:
- 熟悉树和二叉树的有关概念
- 熟悉二叉树的性质
- 熟练掌握遍历二叉树的递归算法,并灵活运用
- 递归遍历二叉树及其应用
本文着重在树和二叉树实际应用与代码实现基本操作,对概念就不再赘述
2 - 二叉树的存储结构
2.1 - 顺序储存结构
二叉树可以用数组存储,编号i的节点存放在[i-1]处,适合于存储完全二叉树
让我们看一道例题来感受一下用数组怎么使用二叉树。
例题2-1 小球下落(Dropping Balls, UVa 679)
有一棵二叉树,最大深度为D,且所有叶子的深度都相同。所有结点从上到下从左到右
编号为1, 2, 3,…, 2D-1。在结点1处放一个小球,它会往下落。每个内结点上都有一个开关,
初始全部关闭,当每次有小球落到一个开关上时,状态都会改变。当小球到达一个内结点
时,如果该结点上的开关关闭,则往左走,否则往右走,直到走到叶子结点,如图所
示。
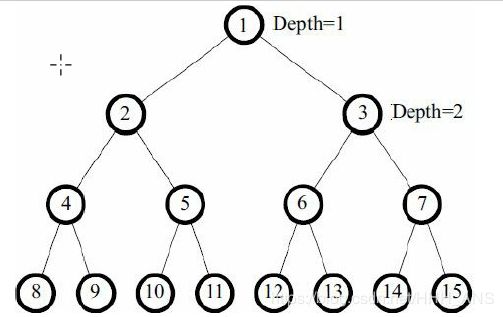
一些小球从结点1处依次开始下落,最后一个小球将会落到哪里呢?输入叶子深度D和
小球个数I,输出第I个小球最后所在的叶子编号。假设I不超过整棵树的叶子个数。D≤20。
输入最多包含1000组数据。
样例输入:
4 2
3 4
10 1
2 2
8 128
16 12345
样例输出:
12
7
512
3
255
36358
【分析】
这道题目是一道简单的构造二叉树的题目,然后只需加入开关判断是进入左子树还是右子树即可。
在使用数组构建二叉树的时候,我们要清楚的知道二叉树的基本性质
- 二叉树的第i层上至多有 2 i − 1 2^{i-1} 2i−1个结点。
- 深度为k的二叉树至多有 2 k − 1 2^k-1 2k−1个结点
- 叶子结点 n 0 n_0 n0,度为2的结点为 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
- n个结点的完全二叉树深度为 ⌊ l o g n ⌋ + 1 \left \lfloor logn \right \rfloor+1 ⌊logn⌋+1
- n个结点的完全二叉树,节点按层次编号
有:i的双亲是 ⌊ n / 2 ⌋ + 1 \left \lfloor n/2\right \rfloor+1 ⌊n/2⌋+1,如果i=1时为根(无双亲);
i的左孩子是2i,如果2i>n,则无左孩子
i的右孩子是2i+1,如果2i+1>n则无右孩子。
在知道这些性质之后,我们不难写出一个数组二叉树来模拟题目操作
#include
#include
const int maxd = 20;
int s[1 << maxd]; //最大节点个数为2^maxd-1
int main()
{
int D, I;
while(scanf_s("%d%d",&D,&I)==2){
memset(s, 0, sizeof(s)); //初始化开关
int k, n = (1 << D) - 1; //n是最大节点编号
for(int i = 0;i n) break; //已经落“出界了”
}
}
printf("%d\n", k / 2); //“出界”之前的叶子编号
}
return 0;
}
2.2 - 二叉树的链式结构
但是在实际操作中,我们用的更多的是链式结构来生成二叉树
首先让我们来看一下二叉树结点的链表结构定义:
typedef struct BTNode{
int data;
struct BTNode *lchild;
struct BTNode *rchild;
}BiTNode,*BiTree;
在定义了结点后,我们就可以使用这个结构来构建二叉树,并且对二叉树进行基本的操作和访问。
#include
#include
#include
using namespace std;
typedef struct BTNode{
int data;
struct BTNode *lchild;
struct BTNode *rchild;
}BiTNode,*BiTree;
int CreateBiTree(BiTree *T){
int ch;
cin >> ch;
if(ch == -1)
{
*T = NULL;
return 0;
}
else
{
*T = (BiTree)malloc(sizeof(BiTNode));
if(T == NULL)
{
printf("failed\n");
return 0;
}
else
{
(*T)->data = ch;
printf("输入%d的左子节点:",ch);
CreateBiTree(&((*T)->lchild));
printf("输入%d的右子节点:", ch);
CreateBiTree(&((*T)->rchild));
}
}
return true;
}
void PreOrderBiTree(BiTree T)
{
if (T == NULL)
{
return;
}
else
{
printf("%d ", T->data);
PreOrderBiTree(T->lchild);
PreOrderBiTree(T->rchild);
}
}
void MiddleOrderBiTree(BiTree T)
{
if (T == NULL)
{
return;
}
else
{
MiddleOrderBiTree(T->lchild);
printf("%d ", T->data);
MiddleOrderBiTree(T->rchild);
}
}
void PostOrderBiTree(BiTree T)
{
if (T == NULL)
{
return;
}
else
{
PostOrderBiTree(T->lchild);
PostOrderBiTree(T->rchild);
printf("%d ", T->data);
}
}
int main()
{
BiTree T;
cout << "请输入根节点:\n";
CreateBiTree(&T);
printf("先序遍历二叉树:");
PreOrderBiTree(T);
printf("\n");
printf("中序遍历二叉树:");
MiddleOrderBiTree(T);
printf("\n");
printf("后序遍历二叉树:");
PostOrderBiTree(T);
printf("\n");
return 0;
}
让我们将上图的二叉树输入这个程序观察输出结果(输入时,当结点没有子节点则输入-1)
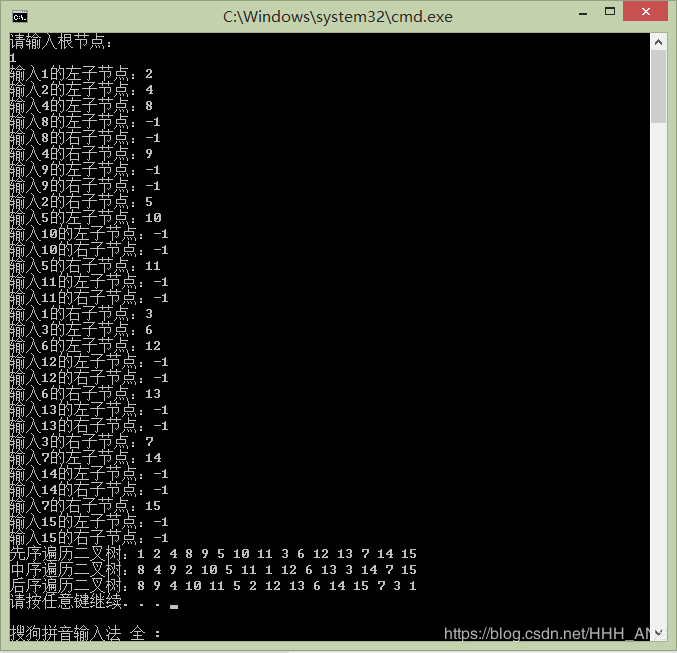
下面让我们看一道例题如何使用层遍历
树的层次遍历(Trees on the level, Duke 1993, UVa 122)
输入一棵二叉树,你的任务是按从上到下、从左到右的顺序输出各个结点的值。每个结
点都按照从根结点到它的移动序列给出(L表示左,R表示右)。在输入中,每个结点的左
括号和右括号之间没有空格,相邻结点之间用一个空格隔开。每棵树的输入用一对空括
号“()”结束(这对括号本身不代表一个结点),如图所示。
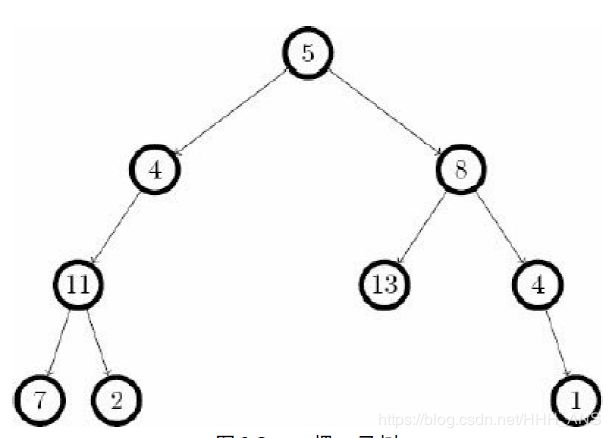
注意,如果从根到某个叶结点的路径上有的结点没有在输入中给出,或者给出超过一
次,应当输出-1。结点个数不超过256。
样例输入:
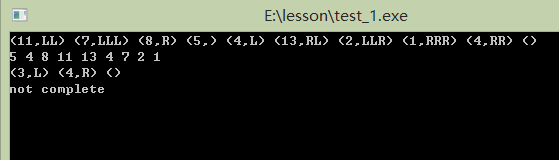
(11,LL) (7,LLL) (8,R) (5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()
样例输出:
5 4 8 11 13 4 7 2 1
-1
【分析】
-
1.用结构链表来建树
-
2.用队列来实现层次遍历,当遍历到根节点时,将其子节点压入队列
#include
#include
#include
#include
#include
#include
using namespace std;
//树结点
struct Node{
int v ;
Node* left,*right ;
int have_value ;
Node():have_value(false),left(NULL),right(NULL){} ;
} ;
Node* root ;//根节点
Node* newnode(){
return new Node() ; //返回一个新结点
}
bool failed ;
void addnode(int v,char* s){//添加新结点
int n = strlen(s);
Node* u = root ;
for(int i = 0;i < n;i++)//找到要加入的位置
{
if(s[i] == 'L'){
if(u->left == NULL) u->left = newnode();
u = u->left;
}
else if(s[i] == 'R'){
if(u->right == NULL) u->right= newnode();
u = u->right ;
}
}
if(u->have_value) failed = true ;//是否已经被访问过;
u->v = v;
u->have_value = true;
}
void freetree(Node* u){ //释放内存
if(u == NULL) return ;
freetree(u->left);
freetree(u->right);
delete u;
}
char s[1005];
bool read_input(){
failed = false ;
freetree(root) ;
root = newnode();
while(true){
if(scanf("%s", s) != 1) return false;
if(!strcmp(s,"()")) break;
int v ;
sscanf(&s[1],"%d",&v);
addnode(v,strchr(s,',')+1);
}
return true ;
}
bool bfs(vector& ans){//搜索
queue q;
ans.clear();
q.push(root);
while(!q.empty()){
Node *u = q.front();q.pop();
if(!u->have_value) return false;
ans.push_back(u->v);
if(u->left != NULL) q.push(u->left);
if(u->right != NULL) q.push(u->right);
}
return true ;
}
int main(int argc, char *argv[])
{
vector ans;
while(read_input()){
if(!bfs(ans)) failed = 1;
if(failed) printf("not complete\n");
else{
for(int i = 0;i < ans.size();i++)
{
if(i != 0) cout << " " ;
cout << ans[i];
}
cout << endl ;
}
}
return 0;
}