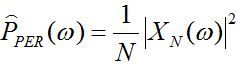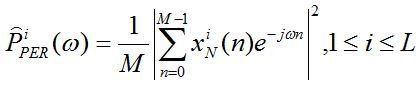几种常用的经典频谱估计方法原理介绍及Matlab算法实现
在信号的谱分析中，由于经典的谱分析方法物理意义比较明确，能够处理的信号信噪比可以很低（相对于现代的谱估计来说），而且处理算法简单稳定；因此在大多数的情况下都是使用经典的谱分析方法对信号进行谱分析。
经典的谱分析方法有：直接法、间接法、Bartlett法和Welch法。下面就来分别讨论这几种方法的特点。
直接法
直接法又称周期图法，它是把随机信号x(n)的N点观察数据
视为一个能量有限的信号，直接取的傅里叶变换，得
，然后再取其幅值的平方，并除以N，作为对x(n)真实的功率谱
的估计。以
表示用周期图法估计出的功率谱，则有
间接法
此方法又称自相关法或者BT法，此方法的理论基础是维纳-辛钦定理，即先由估计出自相关函数
求傅里叶变换得到的功率谱，记之为
，并以此作为对
的估计，即
Bartlett法
由概率论可知，对L个具有相同的均值
和方差
的独立随机变量
,新的随机变量
的均值也是，但方差是
为原来的1/L。由此我们可以得到改善
方差特性的一个有效的方法，即Bartlett法。Bartlett法将采样数据分成L段，每段长度都是M，即N=LM，第i段数据加矩形窗后，变为
式中
是长度为M的矩形窗口。分别计算每一段的功率谱
，即
把对应相加，再取平均，得到平均周期图
，即
Welch法
Welch法是对Bartlett法的改进。改进之一是，在对分段时，可允许每一段的数据有部分的交叠。改进之二是，每一段的数据窗口可以不是矩形窗口，例如使用汉宁窗或汉明窗。这样可以改善由于矩形窗旁瓣较大所产生的谱失真。然后按Bartlett法求每一段的功率谱。
Matalb仿真
为了对比这几种方法的优缺点，在仿真的程序中保持分析的信号不变，分别利用上述的方法进行分析。
生成两种不同频率的正弦信号频率分别为150KHz、140KHz。采样率为750KHz，采样点数为512个点，信噪比为20dB。
Matlab程序如下：
clear all;
close all;
clc;
f0 = 150e3; %定义信号的频率
f1 = 140e3;
fs = 5*f0; %定义采样率
points = 512; %采样点数
signal_points = 512; %信号的长度
SNR = 20; %信噪比
nTs = (0:points-1)/fs;
Delta_f = (0:points-1)*fs/points;
signal = sin(2*pi*f0*nTs)+sin(2*pi*f1*nTs);
signal(signal_points:points) = 0;
signal_noise = signal + 10^(-SNR/20)*randn(1,points);直接法的Matlab程序
首先计算截断的信号的离散傅里叶变换，然后取模值的平方并归一化，最后取以10为底的对数然后乘以10，绘制归一化后的功率谱图。
fft_signal_noise = fft(signal_noise);
squar_fft_signal_noise = fft_signal_noise.*conj(fft_signal_noise);
Periodogram_method_Spectrum = squar_fft_signal_noise/points;
max_Periodogram_method_Spectrum = max(Periodogram_method_Spectrum); %求行最大值
Periodogram_method_Spectrum = Periodogram_method_Spectrum/max_Periodogram_method_Spectrum;
log10_Periodogram_method_Spectrum = 10*log10(Periodogram_method_Spectrum);
figure;
plot(Delta_f(1:points/2)/1000,log10_Periodogram_method_Spectrum(1:points/2));
xlabel('KHz');
ylabel('归一化功率谱P(k)/dB');
string = ['直接法（周期图法）信号点数=',num2str(signal_points),',采样点数=',num2str(points),...
',信号频率=',num2str(f0/1000),'KHz,采样率=',num2str(fs/1000),'KHz,信噪比SNR=',...
num2str(SNR),'dB'];
title(string);BT法的Matlab程序
首先计算截断信号的线性自相关，然后求其离散傅里叶变换，取其模值，归一化，并取以10为底的对数然后乘以10，绘制归一化后的功率谱图。
autocorr_signal_noise = xcorr(signal_noise); %求线性自相关
fft_autocorr_signal_noise = fft(autocorr_signal_noise); %求自相关的fft
abs_fft_autocorr_signal_noise = abs(fft_autocorr_signal_noise)/(2*points-1); %求幅值
max_abs_fft_autocorr_signal_noise = max(abs_fft_autocorr_signal_noise);
abs_fft_autocorr_signal_noise = abs_fft_autocorr_signal_noise/max_abs_fft_autocorr_signal_noise;
log10_abs_fft_autocorr_signal_noise = 10*log10(abs_fft_autocorr_signal_noise);
Delta_f1 = (0:2*points-2)*fs/(2*points-1);
figure;
plot(Delta_f1(1:points)/1000,log10_abs_fft_autocorr_signal_noise(1:points));
xlabel('KHz');
ylabel('归一化功率谱P(k)/dB');
string = ['间接法（自相关法BT）信号点数=',num2str(signal_points),',采样点数=',num2str(points),...
',信号频率=',num2str(f0/1000),'KHz,采样率=',num2str(fs/1000),'KHz,信噪比SNR=',...
num2str(SNR),'dB'];
title(string);Bartlett法的Matlab程序
首先将截断的信号分成等长的不重叠的若干段，然后计算每一段的离散傅里叶变换，并取模值的平方，然后对应点求和。所有段计算并求和完成后，归一化处理，并取以10为底的对数然后乘以10，绘制归一化后的功率谱图。
M = 128; %每段的点数
L = points/M; %段数
Bartlett_Spectrum = zeros(1,points);
for i=1:L
temp_signal = zeros(1,points); %清零
start_point = (i-1)*M;
temp_signal(1:M) = signal_noise((start_point+1):(start_point+M)); %截取第i段信号
fft_temp_signal = fft(temp_signal);
squar_fft_temp_signal = fft_temp_signal.*conj(fft_temp_signal); %求当前段的功率谱
Bartlett_Spectrum = Bartlett_Spectrum + squar_fft_temp_signal; %累加
end
max_Bartlett_Spectrum = max(Bartlett_Spectrum);
Bartlett_Spectrum = Bartlett_Spectrum/max_Bartlett_Spectrum; %归一化
log10_Bartlett_Spectrum = 10*log10(Bartlett_Spectrum); %求对数
Delta_f2 = (0:points-1)*fs/points;
figure;
plot(Delta_f2(1:points/2)/1000,log10_Bartlett_Spectrum(1:points/2));
xlabel('KHz');
ylabel('归一化功率谱P(k)/dB');
string = ['Bartlett法,信号点数=',num2str(signal_points),',采样点数=',num2str(points),...
',信号频率=',num2str(f0/1000),'KHz,采样率=',num2str(fs/1000),'KHz,信噪比SNR=',...
num2str(SNR),'dB,段数L=',num2str(L),',每段点数M=',num2str(M)];
title(string);Welch法的Matlab程序
首先将截断的信号分成等长的有重叠的若干段，然后计算每一段的离散傅里叶变换，并取模值的平方，然后对应点求和。所有段计算并求和完成后，归一化处理，并取以10为底的对数然后乘以10，绘制归一化后的功率谱图。
M = 128; %每段的点数
Overlap = M-M/16; %重叠点数
L = (points - Overlap)/(M-Overlap); %段数
Welch_Spectrum = zeros(1,points);
for i=1:L
temp_signal = zeros(1,points); %清零
start_point = (i-1)*(M-Overlap);
temp_signal(1:M) = signal_noise((start_point+1):(start_point+M)); %截取第i段信号
fft_temp_signal = fft(temp_signal);
squar_fft_temp_signal = fft_temp_signal.*conj(fft_temp_signal); %求当前段的功率谱
Welch_Spectrum = Welch_Spectrum + squar_fft_temp_signal; %累加
end
max_Welch_Spectrum = max(Welch_Spectrum);
Welch_Spectrum = Welch_Spectrum/max_Welch_Spectrum; %归一化
log10_Welch_Spectrum = 10*log10(Welch_Spectrum); %求对数
Delta_f3 = (0:points-1)*fs/points;
figure;
plot(Delta_f3(1:points/2)/1000,log10_Welch_Spectrum(1:points/2));
xlabel('KHz');
ylabel('归一化功率谱P(k)/dB');
string = ['Welch法,信号点数=',num2str(signal_points),',采样点数=',num2str(points),...
',信号频率=',num2str(f0/1000),'KHz,采样率=',num2str(fs/1000),'KHz,信噪比SNR=',...
num2str(SNR),'dB,段数L=',num2str(L),',每段点数M=',num2str(M),',重叠点数=',...
num2str(Overlap)];
title(string);Matlab运行结果及分析
设置相应参数运行上述程序得到如下图：
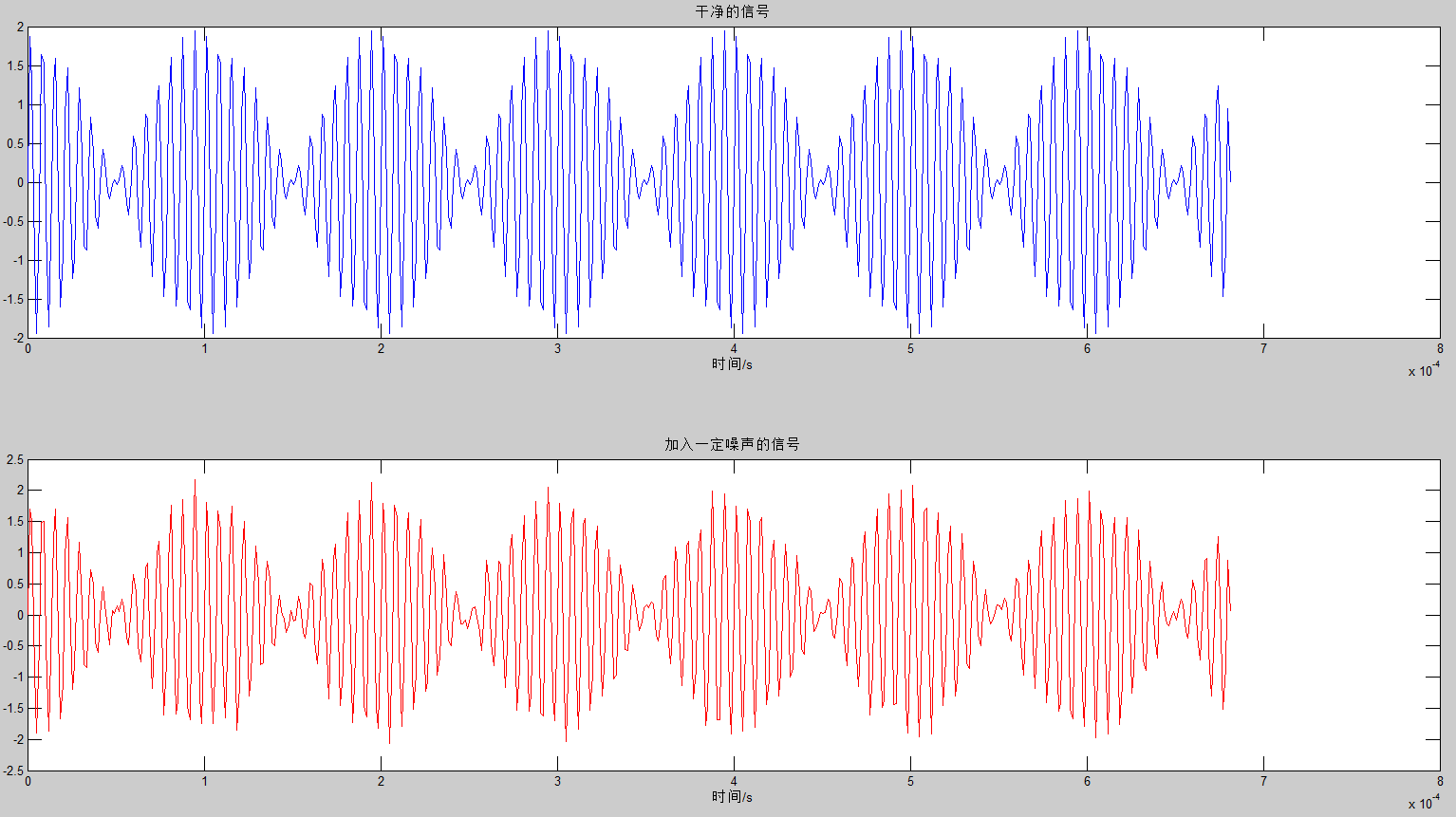
图1信号的时域图
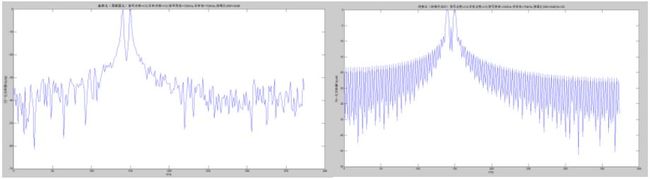
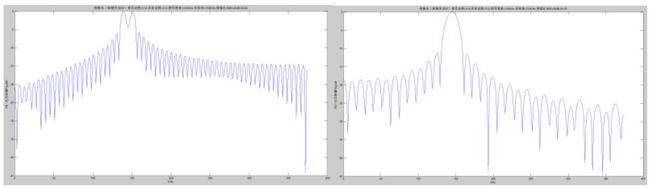
图2周期图法得到的功率谱图 图3 BT法得到的功率谱(M=128)
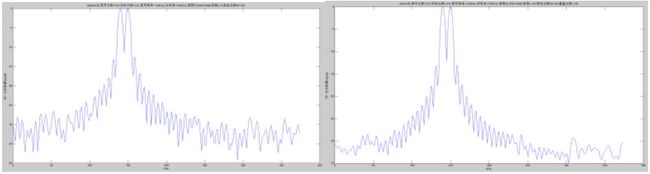
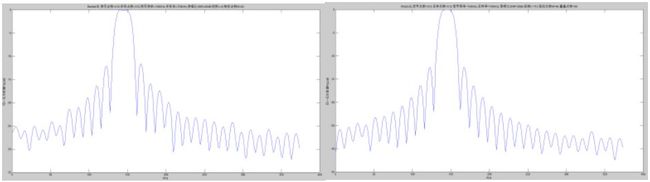
图4 Batlett法得到的功率谱（4段） 图5 Welch法得到的功率谱(128点)
图6 BT法得到的功率谱(M=64) 图7 BT法得到的功率谱(M=32)
图8 Batlett法得到的功率谱（8段） 图9 Welch法得到的功率谱(64点)
图1为生成的仿真信号，一共512个点。
图2为用周期图法对数据直接求出功率谱。由于主瓣宽度B = 2/512 = 0.003906 < (150-140)/750 = 0.013所以f0与f1能够分开。
图3是利用BT法求出的功率谱，M=128,依然能将f0与f1分开；对于与图2其主瓣更宽了。当M=64时，如图6 f0与f1不能完全分开，只是在波形的顶部看出是两个频率的分量。当M=32,如图7 f0与f1就已经无法分开了。
图4是利用Batlett法求出的功率谱，共分4段，每段128个点，可以看到f0与f1能够被分开，相对于图2其更加平滑，但是主瓣的宽度比图2的要宽。当分为8段，每段64个点时，如图8其变的更加平滑但f0与f1已经不能完全分开了。
图5是利用Welch方法求出的平均周期图，每段128个点，重合120个点，谱变得更加的平滑，效果与图4基本一致。若每段64个点，重合60个点，如图9 f0与f1已不能分开，效果与图8基本一致。
结论
综合上述讨论，可以得到对经典谱估计如下总结：
1．经典谱估计可以用FFT快速计算，且物理概念明确，因而仍是目前很常用的谱估计方法。
2. 谱的分辨率较低，它正比于，N是所使用的数据长度。
3. 由于不可避免的窗函数的影响，使得真正谱在窗口主瓣内的功率向旁瓣部分“泄露”，降低了分辨率。较大旁瓣有可能掩盖中较弱的成分，或是产生假的峰值。当分析的数据较短时，这些影响更为突出。
4. 方差性能不好，不是的一致估计，且N增大时谱线起伏加剧。
5.周期图的平滑和平均是和窗函数的使用紧紧相关联的。平滑和平均主要是用来改善周期图的方差性能，但往往又降低了分辨率和增大了偏差。没有一个窗函数能使估计的谱在方差、偏差和分辨率这几个方面都得到改善。因此，使用窗函数只是改进估计质量的一个技巧问题，而不是根本的解决办法。