【机器学习降维】拉普拉斯矩阵与谱聚类
文章目录
- 1.拉普拉斯矩阵
- 1.1 简介
- 1.2 性质
- 2. 瑞利熵
- 3.广义瑞利熵
- 4.谱聚类
- 4. Laplacian Eigenmaps
1.拉普拉斯矩阵
1.1 简介
拉普拉斯矩阵(Laplacian matrix),也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图G=(V,E),其拉普拉斯矩阵定义为:
L = D − W L=D-W L=D−W
其中W为图G的邻接矩阵,一个 N × N N \times N N×N的矩阵,记录每个点与其他点是否相邻,相邻则对应的位置置1。D为图G的度矩阵,将W矩阵的每一列相加后放在对角上,就得到了度矩阵D,它只有对角线上的值非0。拉普拉斯矩阵定义为L=D-W,若 W = [ 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 ] W=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0\end{bmatrix} W=⎣⎢⎢⎡0100101001010010⎦⎥⎥⎤,则 D = [ 1 0 0 0 0 2 0 0 0 0 2 0 0 0 0 1 ] D=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} D=⎣⎢⎢⎡1000020000200001⎦⎥⎥⎤,其拉普拉斯矩阵 L = [ 1 − 1 0 0 − 1 2 − 1 0 0 − 1 2 − 1 0 0 − 1 1 ] L=\begin{bmatrix} 1 & -1 & 0 & 0 \\ -1 & 2 & -1 & 0 \\ 0 & -1 & 2 & -1 \\ 0 & 0 & -1 & 1\end{bmatrix} L=⎣⎢⎢⎡1−100−12−100−12−100−11⎦⎥⎥⎤。
1.2 性质
拉普拉斯矩阵L的性质如下:
- L是对称半正定矩阵
- L的最小特征值为0,对应的特征向量为 1 ⃗ \vec 1 1(对L做初等行变化易知矩阵L不满秩,从而存在特征值0,将每一行相加得到0,从而特征向量为全1向量)
- L有n个非负实特征值。
- 对任何一个实向量f,有 f ′ L f = 1 2 ∑ i , j = 1 N w i j ( f i − f j ) 2 f'Lf=\frac{1}{2}\sum_{i,j=1}^Nw_{ij}(f_i-f_j)^2 f′Lf=21∑i,j=1Nwij(fi−fj)2成立。
性质4的证明如下:
f ′ L f = f ′ D f − f ′ W f = ∑ i = 1 N d i f i 2 − ∑ i , j = 1 N f i f j w i j = 1 2 ( ∑ i = 1 N d i f i 2 + ∑ j = 1 N d j f j 2 − 2 ∑ i , j = 1 N f i f j w i j ) = 1 2 ∑ i , j = 1 N w i j ( f i − f j ) 2 \begin{aligned} f'Lf &=f'Df-f'Wf=\sum_{i=1}^Nd_if_i^2-\sum_{i,j=1}^Nf_if_jw_{ij}\\ &=\frac{1}{2}\left(\sum_{i=1}^Nd_if_i^2+\sum_{j=1}^Nd_jf_j^2-2\sum_{i,j=1}^Nf_if_jw_{ij}\right)\\ &=\frac{1}{2}\sum_{i,j=1}^Nw_{ij}(f_i-f_j)^2 \end{aligned} f′Lf=f′Df−f′Wf=i=1∑Ndifi2−i,j=1∑Nfifjwij=21(i=1∑Ndifi2+j=1∑Ndjfj2−2i,j=1∑Nfifjwij)=21i,j=1∑Nwij(fi−fj)2
2. 瑞利熵
R ( A , x ) = x T A x x T x R(A,x)=\frac{x^TAx}{x^Tx} R(A,x)=xTxxTAx
x是一个向量,A是一个共轭对称矩阵,有 A i j = A j i ∗ A_{ij}=A_{ji}^* Aij=Aji∗,如果A是实矩阵,则 A T = A A^T=A AT=A。该式子的特点是最大值和最小值分别等于矩阵A最大和最小的特征值。即
λ m i n ≤ R ( A , x ) ≤ λ m a x \lambda_{min} \le R(A,x) \le \lambda_{max} λmin≤R(A,x)≤λmax
由于 x T x x^Tx xTx是一个数,若要求R(A,x)的最大值,可以看成是
max R ( A , x ) = max x T A x s . t . x T x = c \max {R(A,x)}=\max x^TAx \quad s.t. \quad x^Tx=c maxR(A,x)=maxxTAxs.t.xTx=c
用拉格朗日乘子法求得极值,其过程如下:
J ( x ) = x T A x − λ ( x T x − c ) ∂ J ( x ) ∂ x = 0 → A x = λ x R ( A , x ) = x T A x x T x = x T λ x x T x = λ J(x)=x^TAx-\lambda(x^Tx-c) \\ \frac{\partial J(x)}{\partial x}=0 →Ax=\lambda x \\ R(A,x)=\frac{x^TAx}{x^Tx}=\frac{x^T\lambda x}{x^Tx}=\lambda J(x)=xTAx−λ(xTx−c)∂x∂J(x)=0→Ax=λxR(A,x)=xTxxTAx=xTxxTλx=λ
此时x为矩阵A的特征值 λ \lambda λ对应的特征向量,根据上述推导可知R(A,x)的最大值就是A的最大特征值,最小值就是A的最小特征值,对应的解就是对应的特征向量。
3.广义瑞利熵
R ( A , B , x ) = x T A x x T B x R(A,B,x)=\frac{x^TAx}{x^TBx} R(A,B,x)=xTBxxTAx
x是一个向量,A,B分别是共轭对称矩阵。同瑞利熵的推导,用拉格朗日乘子法求得极值,其过程如下:
J ( x ) = x T A x − λ ( x T B x − c ) ∂ J ( x ) ∂ x = 0 → A x = λ B x J(x)=x^TAx-\lambda(x^TBx-c) \\ \frac{\partial J(x)}{\partial x}=0 →Ax=\lambda Bx \\ J(x)=xTAx−λ(xTBx−c)∂x∂J(x)=0→Ax=λBx
令 x = B − 1 / 2 f x=B^{-1/2}f x=B−1/2f
有
A B − 1 / 2 f = λ B 1 / 2 f ⟺ B − 1 / 2 A B − 1 / 2 f = λ f AB^{-1/2}f=\lambda B^{1/2}f \iff B^{-1/2}AB^{-1/2}f=\lambda f AB−1/2f=λB1/2f⟺B−1/2AB−1/2f=λf
于是,经过一步转换后,广义瑞利熵又可以转换为瑞利熵的形式
R ( A , B , x ) = x T A x x T B x = f T ( B − 1 / 2 A B − 1 / 2 ) f f T f = f T λ f f T f = λ R(A,B,x)=\frac{x^TAx}{x^TBx}=\frac{f^T(B^{-1/2}AB^{-1/2})f}{f^Tf}=\frac{f^T\lambda f}{f^Tf}=\lambda R(A,B,x)=xTBxxTAx=fTffT(B−1/2AB−1/2)f=fTffTλf=λ
4.谱聚类
聚类就是要将一堆没有标签的样本进行合理的划分。在图论的角度上,聚类就是对图进行分割,而谱聚类就是要找到一个合理的切割方法,使得分割后的不同子图内部,权重之和要尽可能地高,而不同子图之间的权重尽可能低。如何切割才能得到最好的结果呢?
我们知道邻接矩阵W代表了点和点之间的连接状态,而上面我们只是简单地令1表示连接,0表示没有边相连。但这样的数字并不能够作为权重。我们可以对其做一点改造,使用一个相似性函数 s i m ( i , j ) sim(i,j) sim(i,j)来衡量点i和点j之间的相似程度,我们可以使用RBF(高斯核函数)来定义相似度,它的定义为 s ( x i , x j ) = e x p ( − γ ∣ ∣ x i − x j ∣ ∣ 2 ) s(x_i,x_j)=exp(-\gamma||x_i-x_j||^2) s(xi,xj)=exp(−γ∣∣xi−xj∣∣2),只有当 x i , x j x_i,x_j xi,xj距离很近时,相似度会比较大,如果稍微远一点, x i , x j x_i,x_j xi,xj的相似度下降的比较快。因此只有非常靠近的点会相连。
令 A 1 , A 2 , . . . A K A_1,A_2,...A_K A1,A2,...AK表示图的几个不相交子集, A ˉ i \bar A_i Aˉi表示 A i A_i Ai的补集, W ( A i , A ˉ i ) W(A_i,\bar A_i) W(Ai,Aˉi)表示 A i A_i Ai和 A ˉ i \bar A_i Aˉi之间所有边的权重之和。为了让分割的Cut值最小,谱聚类的目标函数定义如下:
C u t ( A 1 , . . . , A K ) = 1 2 ∑ i = 1 K W ( A i , A ˉ i ) Cut(A_1,...,A_K)=\frac{1}{2}\sum_{i=1}^KW(A_i,\bar A_i) Cut(A1,...,AK)=21i=1∑KW(Ai,Aˉi)
然而最小化这个目标函数并不一定能够得到最佳的结果,比如下面这种情况,最小化上面的目标函数往往会得到一个较为偏斜的结果。
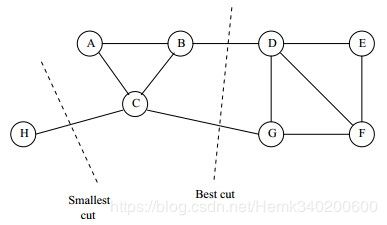
为了让每个类尽量合理,让 A 1 , A 2 , . . . A K A_1,A_2,...A_K A1,A2,...AK都尽量大,改进后的目标函数为( ∣ A i ∣ |A_i| ∣Ai∣表示i类里包含的定点个数):
R a t i o C u t ( A 1 , . . . , A K ) = 1 2 ∑ i = 1 K c u t ( A 1 , . . . , A K ) ∣ A i ∣ RatioCut(A_1,...,A_K)=\frac{1}{2}\sum_{i=1}^K\frac{cut(A_1,...,A_K)}{|A_i|} RatioCut(A1,...,AK)=21i=1∑K∣Ai∣cut(A1,...,AK)
也有另外一种优化方式如下:
N c u t ( A 1 , . . . , A K ) = 1 2 W ( A i , A ˉ i ) ∑ i ∈ A i w i j Ncut(A_1,...,A_K)=\frac{1}{2}\frac{W(A_i,\bar A_i)}{\sum_{i \in A_i}w_{ij}} Ncut(A1,...,AK)=21∑i∈AiwijW(Ai,Aˉi)
定义向量 f = ( f 1 , . . . , f n ) ∈ R n f=(f_1,...,f_n) \in R^n f=(f1,...,fn)∈Rn,且 f i = { ∣ A ˉ ∣ ∣ A ∣ v i ∈ A − ∣ A ∣ ∣ A ˉ ∣ v i ∈ A ˉ f_i=\begin{cases}\sqrt{\frac{|\bar A|}{|A|}} & v_i \in A \\ -\sqrt{\frac{|A|}{|\bar A|}} & v_i \in \bar A \end{cases} fi=⎩⎨⎧∣A∣∣Aˉ∣−∣Aˉ∣∣A∣vi∈Avi∈Aˉ,根据拉普拉斯矩阵性质4,有
f ′ L f = 1 2 ∑ i , j = 1 N w i j ( f i − f j ) 2 = 1 2 ∑ i ∈ A , j ∈ A ˉ w i j ( ∣ A ˉ ∣ ∣ A ∣ + ∣ A ∣ ∣ A ˉ ∣ ) 2 + 1 2 ∑ i ∈ A , j ∈ A ˉ w i j ( − ∣ A ˉ ∣ ∣ A ∣ − ∣ A ∣ ∣ A ˉ ∣ ) 2 = 1 2 ∑ i ∈ A , j ∈ A ˉ w i j ( ∣ A ˉ ∣ ∣ A ∣ + ∣ A ∣ ∣ A ˉ ∣ ) 2 + 1 2 ∑ i ∈ A , j ∈ A ˉ w i j ( − ∣ A ˉ ∣ ∣ A ∣ − ∣ A ∣ ∣ A ˉ ∣ ) 2 = c u r ( A , A ˉ ) ( ∣ A ˉ ∣ ∣ A ∣ + ∣ A ∣ ∣ A ˉ ∣ + 2 ) = c u r ( A , A ˉ ) ( ∣ A ˉ ∣ + ∣ A ∣ ∣ A ∣ + ∣ A ∣ + ∣ A ˉ ∣ ∣ A ˉ ∣ ) = c u r ( A , A ˉ ) ( ∣ V ∣ ∣ A ∣ + ∣ V ∣ ∣ A ˉ ∣ ) = ∣ V ∣ c u r ( A , A ˉ ) ( 1 ∣ A ∣ + 1 ∣ A ˉ ∣ ) = n × R a t i o C u t ( A , A ˉ ) \begin{aligned} f'Lf &=\frac{1}{2}\sum_{i,j=1}^Nw_{ij}(f_i-f_j)^2 \\ &=\frac{1}{2}\sum_{i \in A,j \in \bar A}w_{ij}(\sqrt{\frac{|\bar A|}{|A|}}+\sqrt{\frac{|A|}{|\bar A|}})^2+\frac{1}{2}\sum_{i \in A,j \in \bar A}w_{ij}(-\sqrt{\frac{|\bar A|}{|A|}}-\sqrt{\frac{|A|}{|\bar A|}})^2 \\ &=\frac{1}{2}\sum_{i \in A,j \in \bar A}w_{ij}(\sqrt{\frac{|\bar A|}{|A|}}+\sqrt{\frac{|A|}{|\bar A|}})^2+\frac{1}{2}\sum_{i \in A,j \in \bar A}w_{ij}(-\sqrt{\frac{|\bar A|}{|A|}}-\sqrt{\frac{|A|}{|\bar A|}})^2 \\ &=cur(A,\bar A)(\frac{|\bar A|}{|A|}+\frac{|A|}{|\bar A|}+2) \\ &=cur(A,\bar A)(\frac{|\bar A|+|A|}{|A|}+\frac{|A|+|\bar A|}{|\bar A|}) \\ &=cur(A,\bar A)(\frac{|V|}{|A|}+\frac{|V|}{|\bar A|}) \\ &=|V|cur(A,\bar A)(\frac{1}{|A|}+\frac{1}{|\bar A|}) \\ &=n\times RatioCut(A,\bar A) \\ \end{aligned} f′Lf=21i,j=1∑Nwij(fi−fj)2=21i∈A,j∈Aˉ∑wij(∣A∣∣Aˉ∣+∣Aˉ∣∣A∣)2+21i∈A,j∈Aˉ∑wij(−∣A∣∣Aˉ∣−∣Aˉ∣∣A∣)2=21i∈A,j∈Aˉ∑wij(∣A∣∣Aˉ∣+∣Aˉ∣∣A∣)2+21i∈A,j∈Aˉ∑wij(−∣A∣∣Aˉ∣−∣Aˉ∣∣A∣)2=cur(A,Aˉ)(∣A∣∣Aˉ∣+∣Aˉ∣∣A∣+2)=cur(A,Aˉ)(∣A∣∣Aˉ∣+∣A∣+∣Aˉ∣∣A∣+∣Aˉ∣)=cur(A,Aˉ)(∣A∣∣V∣+∣Aˉ∣∣V∣)=∣V∣cur(A,Aˉ)(∣A∣1+∣Aˉ∣1)=n×RatioCut(A,Aˉ)
由于 f i = { ∣ A ˉ ∣ ∣ A ∣ v i ∈ A − ∣ A ∣ ∣ A ˉ ∣ v i ∈ A ˉ f_i=\begin{cases}\sqrt{\frac{|\bar A|}{|A|}} & v_i \in A \\ -\sqrt{\frac{|A|}{|\bar A|}} & v_i \in \bar A \end{cases} fi=⎩⎨⎧∣A∣∣Aˉ∣−∣Aˉ∣∣A∣vi∈Avi∈Aˉ,有
∑ i = 1 n f i = ∣ A ∣ ∣ A ˉ ∣ ∣ A ∣ − ∣ A ˉ ∣ ∣ A ∣ ∣ A ˉ ∣ = 0 ∣ ∣ f ∣ ∣ 2 = ∑ i = 1 n f i 2 = ∣ A ∣ ∣ A ˉ ∣ ∣ A ∣ + ∣ A ˉ ∣ ∣ A ∣ ∣ A ˉ ∣ = ∣ A ˉ ∣ + ∣ A ∣ = n \sum_{i=1}^nf_i=|A|\sqrt{\frac{|\bar A|}{|A|}}-|\bar A|\sqrt{\frac{|A|}{|\bar A|}}=0\\ ||f||^2=\sum_{i=1}^nf_i^2=|A|\frac{|\bar A|}{|A|}+|\bar A|\frac{|A|}{|\bar A|}=|\bar A|+|A|=n i=1∑nfi=∣A∣∣A∣∣Aˉ∣−∣Aˉ∣∣Aˉ∣∣A∣=0∣∣f∣∣2=i=1∑nfi2=∣A∣∣A∣∣Aˉ∣+∣Aˉ∣∣Aˉ∣∣A∣=∣Aˉ∣+∣A∣=n
至此,目标函数变为
min f ∈ R n f ′ L f , ∑ i = 1 n f i = 0 , ∣ ∣ f ∣ ∣ 2 = n \min _{f \in R^n} f'Lf ,\sum_{i=1}^nf_i=0,||f||^2=n f∈Rnminf′Lf,i=1∑nfi=0,∣∣f∣∣2=n
由于 f i f_i fi有两种取值,所以f就有 2 n 2^n 2n种取值,因此找到符合条件的f是一个NP难的问题。为了使问题变得简单,方便求解,我们考虑f为拉普拉斯矩阵L的特征向量的情况。如果 L f = λ f Lf=\lambda f Lf=λf,则有 f ′ L f = λ f ′ f = λ ∣ ∣ f ∣ ∣ 2 = λ n f'Lf=\lambda f'f=\lambda ||f||^2=\lambda n f′Lf=λf′f=λ∣∣f∣∣2=λn,因为n为定值,所以要求最小的 f ′ L f f'Lf f′Lf,只需要找到最小的 λ \lambda λ即可。
由瑞利熵理论可以知道,R(A,x)的最小值为A的最小特征值。不过拉普拉斯矩阵L中,最小的特征值为0对应的特征向量为 1 ⃗ \vec 1 1,不满足 ∑ i = 1 n f i = 0 \sum_{i=1}^nf_i=0 ∑i=1nfi=0,因此我们取第二小的特征值及其对应的特征向量v来作为我们目标函数的解。
由于一开始我们便限制了 f i f_i fi只能有两个取值,而我们得到的特征向量实际上取值为任意实数。一个简单的方法是根据特征向量每个值大于0还是小于0来讲起映射到 f i f_i fi的两个值上,或者用k-means对特征向量v的每一个值进行聚类,相当于做一次1维的聚类,从而将n个点分成二类。
推广到多分类的情况,我们只需要取前k个最小的特征值,将对应的特征向量排列起来( N × K N \times K N×K),在按行进行k-means聚类即可。
4. Laplacian Eigenmaps
上面的推导过程实际上还存在着另外一个应用,那就是Laplacian Eigenmaps,它是一种基于相似度矩阵的降维方法。
Laplacian Eigenmaps 是用局部的角度去构建数据之间的关系。如果两个数据实例i和j很相似,那么i和j在降维后目标子空间中应该尽量接近。它的直观思想是希望相互间有关系的点(在图中相连的点)在降维后的空间中尽可能的靠近。利用上面的推导,我们得到了一个结论:通过找出拉普拉斯矩阵L的最小k个特征值及其对应的特征向量,就可以让切割出来的K个区域内部尽可能地相似,而K个区域之间尽可能地不相似。
Laplacian Eigenmaps的流程其实非常简单,总结如下:
- 使用某种方法将所有点构建成图,如KNN算法。
- 点与点之间的权重点与点之间的权重利用相似度函数来确定。
- 根据得到的图G生成拉普拉斯矩阵L。
- 使用L最小的m个非零特征值对应的特征向量作为降维后的结果输出。