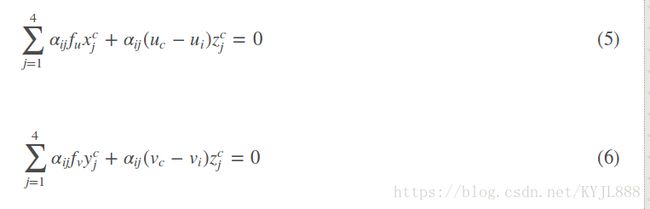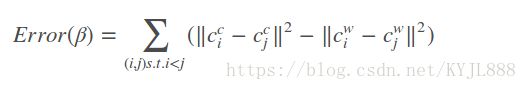Opencv 3.4 的solvepnp中的P3P与EPnp位姿估计算法解析

https://www.cnblogs.com/shang-slam/p/6481344.html

EPnP在ORB-SLAM中主要用于Tracking线程中的重定位Relocalization模块，需要通过当前关键帧Bow与候选帧匹配上的3D地图点，迅速建立当前相机的初始姿态。

PnP问题解决了已知世界参考系下地图点以及相机参考系下投影点位置时3D-2D相机位姿估计问题，不需要使用对极约束（存在初始化，纯旋转和尺度问题，且一般需要8对点），可以在较少的匹配点（最少3对点，P3P方法）中获得较好的运动估计，是最重要的一种姿态估计方法。最后，如果知道世界参考系下的地图点，同时知道相机参考系下的地图点，可以通过ICP的方法去求解姿态。

这样就构成了立体视觉中最重要的对极几何，PnP和ICP三种最常用的姿态估计方法。

---

求解PnP问题目前主要有直接线性变换（DLT），P3P，EPnP，UPnP以及非线性优化方法。

DLT

直接构建一个12个未知数的[R|t]增广矩阵（先不考虑旋转矩阵的自由度只有3），取六个点对，去求解12个未知数（每一个3D点到归一化平面的映射给出两个约束），最后将[R|t]左侧3*3矩阵块进行QR分解，用一个旋转矩阵去近似（将3*3矩阵空间投影到SE(3)流形上）。

P3P

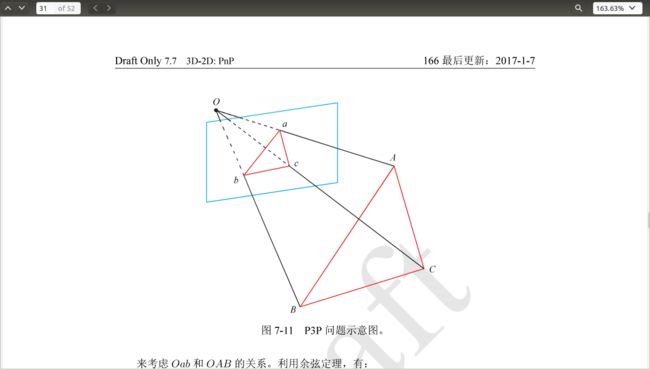
P3P方法是通过3对3D/2D匹配点，求解出四种可能的姿态，在OpenCV calib3d模块中有实现，但是对于相机远离3D平面（low parallax）或者视角垂直于3D平面的情况下效果不佳，不知道最近有没有更新过。论文Complete Solution Classification for the Perspective-Three-Point Problem中提到了一种改进的方法，可以消除这种退化的情况。

将世界坐标系下的ABC三点和图像坐标系下的abc三点匹配，其中AB，BC，AC的长度已知，，，也是已知，通过余弦定理可以求出A，B，C在相机参考系中的坐标，然后使用类似ICP的坐标系对齐，就可以求得当前相机薇姿。

通过余弦定理构建二元二次方程组【2】可以求解出OA，OB，OC之间的长度比例，从而确定世界坐标系下的相机位姿。可以想象一下为什么会出现四个解，在空间中的位置是什么样的，以及为什么在远离3D点平面或者视角垂直3D点平面时，会出现退化情况。

EPnP  需要4对不共面的（对于共面的情况只需要3对）3D-2D匹配点，是目前最有效的PnP求解方法。

The aim of the Perspective-n-Point problem—PnP in short—is to determine the position and orientation of a camera given its intrinsic parameters and a set of n correspondences between 3D points and their 2D projections. It has many applications in Computer Vision, Robotics, Augmented Re- ality and has receivedmuch attention in both the Photogrammetry and Computer Vision communities. In particular, applications such as feature point-based camera tracking require dealing with hundreds of noisy feature points in real-time, which requires computationally efficient methods.

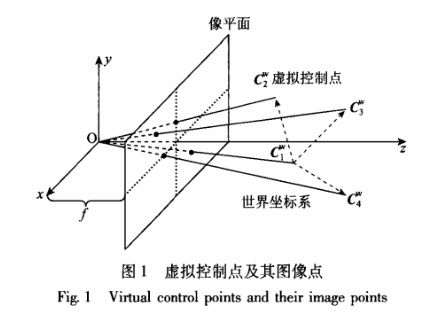
空间中任意3D点的坐标可以用4个不共面的3D点坐标的权重表示

通常选取世界坐标下的四个控制点坐标为Cw=[0,0,0,1]T, [1,0,0,1]T,[0,1,0,1]T,[0,0,1,1]T；通过n个3D点在相机平面的投影关系，以及与这四个控制点的权重关系，构建一个12*12方阵，求得其零空间特征向量，可以得到虚拟控制点的相机平面坐标，然后使用POSIT算法即可求出相机位姿。

通常在用EPnP求得四对点下的封闭解后，可以将该解作为非线性优化的初值，优化提高精度。

主要参考：

1. EPnP:An Accurate O(n) Solution to the PnP problem

2. 高翔，视觉SLAM十四讲

3. http://iplimage.com/blog/p3p-perspective-point-overview/

4. 摄像机位姿的高精度快速求解 

EPnP算法

参考 https://www.cnblogs.com/jian-li/p/5689122.html

EPnP算法

相机坐标系用Fc

，世界坐标系用Fw表示，任何一点可以用四个控制点pwi表示

(1)

对于相机坐标系同样成立

(2)

对于上面的公式，首先需要说明的是αij确实存在。因为cwj或ccj构成的方程组是欠定的，所以一定存在解。
理论上来说，控制点可以随便选择，这里选择控制点为参考点的中心，其他的点在PCA得到的主轴上单位长度处，从而提高算法的稳定性。

控制点在相机坐标系的坐标

根据投影方程得到世界坐标系中参考点坐标和相机坐标系中参考点的约束关系：

 

(3)

写成矩阵的形式为：

(4)

将等式的第三列代入第一二列，得到

因此，可以得到下面的线性方程组：

(7)

上面的方程中，四个控制点总共12个未知变量，M为2n×12的矩阵。因此，x属于M的右零空间，vi为矩阵M的右奇异向量，可以通过求解MTM的零空间特征值得到。

( 8)

[说明]使用MTM比使用M计算量更少，因为MTM是求解是常数复杂度，而M是O(n3)的复杂度，但是计算MTM的复杂度是O(n)

的。

选择合适的线性组合

上面求解的x

中，需要确定βi，也就是确定合适的线性组合。根据参考点的位置不同，矩阵MTM的零空间维数可能为N=1→4维。求解β的策略是控制点在坐标系w和c中，两两之间的距离是相同，而x的3k+1−3k分量表示分别表示不同的控制点在相机坐标系中的坐标，总共有C24=6个约束。
如果N=1，则根据约束有

其中L是由v1和v2构成的6×3的矩阵。
上面的方程可以通过β=(LTL)−1LTρ得到，然后通过选择合适的符号从β21,β1β2,β22使得所有的pci有正的z坐标。

如果N=3 则和N=2差不多，唯一的区别在于使用的是L的逆，而不是伪逆，此时的L为6×6的矩阵。

G-N优化

前面的步骤可以得到目标点在相机坐标系中的闭式解，作为G-N优化的初始值，优化的变量为β=[β1,⋯,βN]T

，目标函数为

(12)

该优化过程和参考点的数目无关，优化步骤和时间是常数。

计算R，t

前面的两步计算不同维数的零空间的误差，选择误差最小维数对应的β

，从而得到x，恢复出控制点在相机坐标系中的坐标并根据质心坐标系数得到参考点在相机坐标系的坐标。剩下的工作就是已知一组点云在两个坐标系中的坐标，求两个坐标系的位姿变换。
步骤如下：

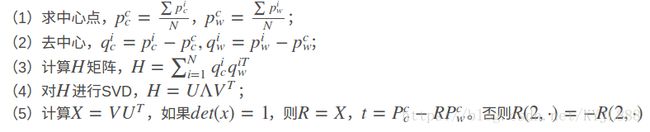
（1）求中心点，pcc=∑picN，pcw=∑piwN；
（2）去中心，qic=pic−pcc,qiw=piw−pcw；
（3）计算H矩阵，H=∑Ni=1qicqiTw
（4）对H进行SVD，H=UΛVT；
（5）计算X=VUT，如果det(x)=1，则R=X，t=Pcc−RPcw。否则R(2,⋅)=−R(2,⋅)

 

这里只介绍opencv3.4 中Epnp算法的头文件，具体内容可以参考论文《EPnP: An Accurate O(n) Solution to the PnP Problem》+opencv3.4 源代码。

参考 https://blog.csdn.net/xuelangwin/article/details/80828762

#ifndef epnp_h
#define epnp_h
 
#include "precomp.hpp"
#include "opencv2/core/core_c.h"
 
namespace cv
{
 
class epnp {
 public:
  /*  max 注释
  *   函数功能：ePnP算法的初始化构造函数，ePnP求解最少需要4对点，而且是相机内参已知
  *             
  *   参数：
  *   [in]    cameraMatrix            相机内参
  *   [in]    opoints                 参考点在世界坐标系中的点，至少4个点-------float or double
  *   [in]    ipoints                 参考点在相机图像上的投影点坐标，至少4个点-------float or double
  *    返回值：
  *           
  */
  epnp(const cv::Mat& cameraMatrix, const cv::Mat& opoints, const cv::Mat& ipoints);
  ~epnp();
 
  // 此函数没有实现---没有使用
  void add_correspondence(const double X, const double Y, const double Z,
              const double u, const double v);
 
  /*  max 注释
  *   函数功能：ePnP算法的初始化构造函数，ePnP求解最少需要4对点，而且是相机内参已知
  *
  *   参数：
  *   [out]    R                 旋转矩阵3x3，世界坐标系到相机坐标系
  *   [out]    t                 平移向量，世界坐标系到相机坐标系
  *    返回值：
  *
  */
  void compute_pose(cv::Mat& R, cv::Mat& t);
 
 
 
 private:
  epnp(const epnp &); // copy disabled
  epnp& operator=(const epnp &); // assign disabled
 
  // 初始化相机内参
  template 
  void init_camera_parameters(const cv::Mat& cameraMatrix)
  {
    uc = cameraMatrix.at (0, 2);
    vc = cameraMatrix.at (1, 2);
    fu = cameraMatrix.at (0, 0);
    fv = cameraMatrix.at (1, 1);
  }
 
 
  // 将输入的世界坐标系的参考点和图像坐标系中的点转化到成员变量存储
  template 
  void init_points(const cv::Mat& opoints, const cv::Mat& ipoints)
  {
      for(int i = 0; i < number_of_correspondences; i++)
      {
          pws[3 * i    ] = opoints.at(i).x;
          pws[3 * i + 1] = opoints.at(i).y;
          pws[3 * i + 2] = opoints.at(i).z;
 
          us[2 * i    ] = ipoints.at(i).x*fu + uc;
          us[2 * i + 1] = ipoints.at(i).y*fv + vc;
      }
  }
 
 
  // 计算世界坐标系的参考点在相机图像坐标系下的投影误差
  double reprojection_error(const double R[3][3], const double t[3]);
 
  // 选择参考坐标系中的控制点，第一个点为质心，第2-4个点PCA中的3个主成分方向上的点
  void choose_control_points(void);
 
  // 计算出论文中的alpha， 灰度质心齐次坐标
  void compute_barycentric_coordinates(void);
 
  // 填充M矩阵，MX=0;
  void fill_M(CvMat * M, const int row, const double * alphas, const double u, const double v);
 
 
  // 根据计算的betas值和对应的特征向量，计算相机坐标系中的控制点
  void compute_ccs(const double * betas, const double * ut);
  // 通过相机坐标系下的控制点，计算所有参考点在相机坐标系下的坐标；
  void compute_pcs(void);
  // 检测参考点在相机坐标系下的z轴坐标是否大于零，大于零不做修改。如果小于零，需要按照相机光心（原点）中心对称一下。
  void solve_for_sign(void);
 
 
  // 假设N=4，就是有4组特征向量的组合来表示解
  void find_betas_approx_1(const CvMat * L_6x10, const CvMat * Rho, double * betas);
  // 假设N=2，就是有2组特征向量的组合来表示解
  void find_betas_approx_2(const CvMat * L_6x10, const CvMat * Rho, double * betas);
  // 假设N=3，就是有3组特征向量的组合来表示解
  void find_betas_approx_3(const CvMat * L_6x10, const CvMat * Rho, double * betas);
  void qr_solve(CvMat * A, CvMat * b, CvMat * X);
 
  double dot(const double * v1, const double * v2);
  double dist2(const double * p1, const double * p2);
 
 
  // 求beta时的rho向量，L*beta=rho
  void compute_rho(double * rho);
 
  // 求beta时的L矩阵（就是论文中N=4时，由最小的四个奇异值所对应的右特征向量所组成) l_6x10 为输出的L矩阵
  void compute_L_6x10(const double * ut, double * l_6x10);
 
  // 高斯牛顿迭代求解，只迭代5次。
  void gauss_newton(const CvMat * L_6x10, const CvMat * Rho, double current_betas[4]);
  // 高斯牛顿中的梯度
  void compute_A_and_b_gauss_newton(const double * l_6x10, const double * rho,
                    const double cb[4], CvMat * A, CvMat * b);
 
  // 计算相机坐标系和世界坐标系之间的变换
  double compute_R_and_t(const double * ut, const double * betas,
             double R[3][3], double t[3]);
 
  // horn 的绝对定向算法
  void estimate_R_and_t(double R[3][3], double t[3]);
 
  void copy_R_and_t(const double R_dst[3][3], const double t_dst[3],
            double R_src[3][3], double t_src[3]);
 
 
  double uc, vc, fu, fv;                              // 相机内参
 
  std::vector pws, us, alphas, pcs;          // pws 参考点在世界坐标系中的坐标； us 对应世界点在图像坐标系上的投影；  alphas 与论文中的一样；pcs 参考点在相机坐标系中的坐标
  int number_of_correspondences;                    // 对应点的个数
 
  double cws[4][3], ccs[4][3];                       //cws 参考坐标系中4个3D参考点；     ccs 相机坐标系中4个3D 参考点
  int max_nr;
  double * A1, * A2;                                // 高斯牛顿使用的量
};
 
}
 
#endif

 

Opencv 3.4 中P3P位姿估计算法解析

来源与  https://blog.csdn.net/xuelangwin/article/details/80769564

先上图，Opencv3.4中用两种算法实现P3P位姿估计问题。一种是基于距离P3P算法问题（算法1：P3P），一种是基于矩阵P3P算法问题（算法2：aP3P），具体推导细节可以参看论文还以整理的本地关键技术文档。此处只对程序进行分析注释，方便以后使用。注意：此处只注释算法2，因为算法1没有完全搞明白（主要是高小山用wu-ritt算法推导我看不太懂）。

外部调用接口函数：

/*  max 注释
*   函数功能：P3P位姿估计的接口函数，此函数可以利用不用的flags值，选择不同的算法。
*             输入3个对应点，返回最多4组有效解
*   参数：
*   [in]    objectPoints                参考坐标系（或世界坐标系）中的3D点，需要3个即可，不要多也不要少。float和double都可以    
*   [in]    imagePoints                 对应3D点在相机相平面上的投影点的图像坐标。需要3个即可，不要多也不要少。注意这个是2D的。float和double都可以
*   [in]    cameraMatrix                相机内参矩阵
*   [in]    distCoeffs                  相机畸变矩阵
*   [out]   rvecs                       输出旋转矩阵,不用声明是多大矩阵-----输出是最多是4个解----每个解的旋转是用旋转向量表示的。------从参考坐标中的点到相机坐标系的点的变换
*   [out]   tvecs                       输出平移矩阵，不用声明多大矩阵------输出最多是4个解。
*   [in]    flags                       选择不同的结算位姿算法，SOLVEPNP_P3P是算法1，采用基于距离PnP算法。SOLVEPNP_AP3P算法2，采用基于矩阵PnP算法。
*
*    返回值：
*            返回解的个数，最大不会超过4个。
*/
int solveP3P(InputArray objectPoints, InputArray imagePoints,	InputArray cameraMatrix, InputArray distCoeffs,	OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs,int flags);

 

测试例子:

#include "test_precomp.hpp"
 
void generate3DPointCloud(std::vector& points, cv::Point3f pmin = cv::Point3f(-1, -1, 5), cv::Point3f pmax = cv::Point3f(1, 1, 10))
{
	cv::RNG rng = cv::theRNG(); // fix the seed to use "fixed" input 3D points
 
	for (size_t i = 0; i < points.size(); i++)
	{
		float _x = rng.uniform(pmin.x, pmax.x);
		float _y = rng.uniform(pmin.y, pmax.y);
		float _z = rng.uniform(pmin.z, pmax.z);
		points[i] = cv::Point3f(_x, _y, _z);
	}
}
 
void generateCameraMatrix(cv::Mat& cameraMatrix, cv::RNG& rng)
{
	const double fcMinVal = 1e-3;
	const double fcMaxVal = 100;
	cameraMatrix.create(3, 3, CV_64FC1);
	cameraMatrix.setTo(cv::Scalar(0));
	cameraMatrix.at(0, 0) = rng.uniform(fcMinVal, fcMaxVal);
	cameraMatrix.at(1, 1) = rng.uniform(fcMinVal, fcMaxVal);
	cameraMatrix.at(0, 2) = rng.uniform(fcMinVal, fcMaxVal);
	cameraMatrix.at(1, 2) = rng.uniform(fcMinVal, fcMaxVal);
	cameraMatrix.at(2, 2) = 1;
}
 
void generateDistCoeffs(cv::Mat& distCoeffs, cv::RNG& rng)
{
	distCoeffs = cv::Mat::zeros(4, 1, CV_64FC1);
	for (int i = 0; i < 3; i++)
		distCoeffs.at(i, 0) = rng.uniform(0.0, 1.0e-6);
}
 
void generatePose(cv::Mat& rvec, cv::Mat& tvec, cv::RNG& rng)
{
	const double minVal = 1.0e-3;
	const double maxVal = 1.0;
	rvec.create(3, 1, CV_64FC1);
	tvec.create(3, 1, CV_64FC1);
	for (int i = 0; i < 3; i++)
	{
		rvec.at(i, 0) = rng.uniform(minVal, maxVal);
		tvec.at(i, 0) = rng.uniform(minVal, maxVal / 10);
	}
}
 
 
int main()
{
	std::vector points;
	points.resize(500);
	generate3DPointCloud(points);
 
 
	std::vector rvecs, tvecs;
	cv::Mat trueRvec, trueTvec;
	cv::Mat intrinsics, distCoeffs;
 
	generateCameraMatrix(intrinsics, cv::RNG());	
	generateDistCoeffs(distCoeffs, cv::RNG());
 
	generatePose(trueRvec, trueTvec, cv::RNG());
 
	std::vector opoints;
	opoints = std::vector(points.begin(), points.begin() + 3);
 
	std::vector projectedPoints;
	projectedPoints.resize(opoints.size());
	projectPoints(cv::Mat(opoints), trueRvec, trueTvec, intrinsics, distCoeffs, projectedPoints);
 
	std::cout << "intrinsics: " << intrinsics << std::endl;
	std::cout << "distcoeffs: " << distCoeffs << std::endl;
	std::cout << "trueRvec: " << trueRvec << std::endl;
	std::cout << "trueTvec: " << trueTvec << std::endl;
 
	std::cout << "oPoint: " << opoints << std::endl;
	std::cout << "projectedPoints: " << projectedPoints << std::endl;
 
 
 
	std::cout<<"result numbers A: :"<

 

算法2中代码描述，下面所描述的不是Opencv外部提供的接口，属于算法的内部实现。---代码在ap3p.h头文件中。

#ifndef P3P_P3P_H
#define P3P_P3P_H
 
#include "precomp.hpp"
 
namespace cv {
class ap3p {
private:
    template
    void init_camera_parameters(const cv::Mat &cameraMatrix) {
        cx = cameraMatrix.at(0, 2);
        cy = cameraMatrix.at(1, 2);
        fx = cameraMatrix.at(0, 0);
        fy = cameraMatrix.at(1, 1);
    }
 
    template
    void extract_points(const cv::Mat &opoints, const cv::Mat &ipoints, std::vector &points) {
        points.clear();
        int npoints = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F));
        points.resize(5*npoints);
        for (int i = 0; i < npoints; i++) {
            points[i * 5] = ipoints.at(i).x * fx + cx;
            points[i * 5 + 1] = ipoints.at(i).y * fy + cy;
            points[i * 5 + 2] = opoints.at(i).x;
            points[i * 5 + 3] = opoints.at(i).y;
            points[i * 5 + 4] = opoints.at(i).z;
        }
    }
 
    void init_inverse_parameters();
 
    double fx, fy, cx, cy;
    double inv_fx, inv_fy, cx_fx, cy_fy;
public:
	// 3个初始化构造函数的目的是获取相机内参数，并且计算相机内参矩阵的逆。---------用于求解论文中的bearing measurement
    ap3p() : fx(0), fy(0), cx(0), cy(0), inv_fx(0), inv_fy(0), cx_fx(0), cy_fy(0) {}
 
    ap3p(double fx, double fy, double cx, double cy);
 
    ap3p(cv::Mat cameraMatrix);
 
 
 
	/*  max 注释
	*   函数功能：此处的位姿估计只返回一个解，并且此处输入的是4个点---注意并不是solveP3P所调用。调用顺序为①-->④-->③
	*   参数：
	*   [out]   R                输出单个旋转矩阵
	*   [out]   tvec             输出单个平移向量
	*   [in]    opoints          输入3D点---4个
	*   [in]    ipoints          输入2D点---4个
	*
	*    返回值：
	*            成功返回true，失败返回false
	*/
    ① bool solve(cv::Mat &R, cv::Mat &tvec, const cv::Mat &opoints, const cv::Mat &ipoints);
 
	/*  max 注释
	*   函数功能：此处的位姿估计只返回最多4个解，是solveP3P所调用。调用顺序为②-->③
	*   参数：
	*   [out]   R                输出最多4个旋转矩阵
	*   [out]   tvec             输出最多4平移向量
	*   [in]    opoints          输入3D点---3个
	*   [in]    ipoints          输入2D点---3个
	*
	*    返回值：
	*            成功返回true，失败返回false
	*/
    ② int solve(std::vector &Rs, std::vector &tvecs, const cv::Mat &opoints, const cv::Mat &ipoints);
 
    ③ int solve(double R[4][3][3], double t[4][3],
              double mu0, double mv0, double X0, double Y0, double Z0,
              double mu1, double mv1, double X1, double Y1, double Z1,
              double mu2, double mv2, double X2, double Y2, double Z2);
 
    ④ bool solve(double R[3][3], double t[3],
               double mu0, double mv0, double X0, double Y0, double Z0,
               double mu1, double mv1, double X1, double Y1, double Z1,
               double mu2, double mv2, double X2, double Y2, double Z2,
               double mu3, double mv3, double X3, double Y3, double Z3);
 
 
	// 此处完全按照论文的计算步骤来的，程序非常清晰，可以参考论文
    // This algorithm is from "Tong Ke, Stergios Roumeliotis, An Efficient Algebraic Solution to the Perspective-Three-Point Problem" (Accepted by CVPR 2017)
    // See https://arxiv.org/pdf/1701.08237.pdf
    // featureVectors: 3 bearing measurements (normalized) stored as column vectors
    // worldPoints: Positions of the 3 feature points stored as column vectors
    // solutionsR: 4 possible solutions of rotation matrix of the world w.r.t the camera frame
    // solutionsT: 4 possible solutions of translation of the world origin w.r.t the camera frame
    int computePoses(const double featureVectors[3][3], const double worldPoints[3][3], double solutionsR[4][3][3],
                     double solutionsT[4][3]);
 
};
}
#endif //P3P_P3P_H