NOIP2013 提高组复赛解题报告
NOIP2013 提高组复赛
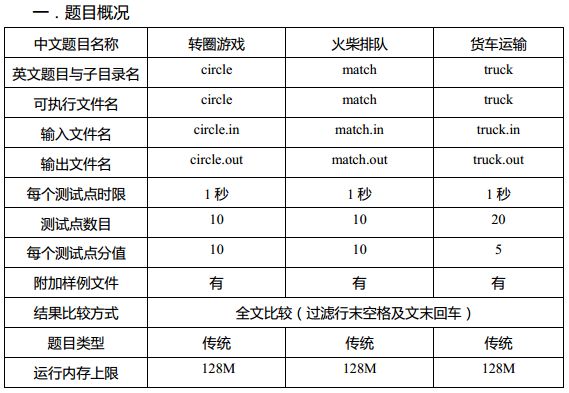
1002. 火柴排队
- 贪心+数据结构/归并排序
这个“相邻交换”让我联想到了NOIP2012_day1_task2_game那题的
恶心做法,于是就专注推导相邻两个元素交换对解的影响。然后根据以前经验知道一定有一个序列可以完全不动,而另一个序列只需要以第一列作为标准移动(所以样例解释反而给的误导很大)。于是很快就确信正解了。现在想起来还有一点小激动,自己居然能找出规律来。
首先,一定可以只对某一组的元素进行交换,能以给定的最少步数,得到另外一组的结果。显然当前序列还缺少k步就和另外一个序列相同时,另外一个序列一定也只需要k步就可以和当前序列相同。
其次,由于只能相邻交换,对于每一次的操作,它对于解的影响一定只与这一对元素有关。于是我们对相邻元素的数量关系进行推导:
假设有两组元素 ai,ai+1 和 bi,bi+1 ,如果有
则说明有 {bi,bi+1} 的顺序比 {bi+1,bi} 更优。对上述式子推导有:
显然上式满足的唯一情况就是 ai>ai+1,bi>bi+1 或 ai<ai+1,bi<bi+1 。也就是说,要求两个序列的元素大小单调且对应。于是我们只要依次配对 a 序列最大,次大…的位置和 b 序列最大,次大…的位置即可。
我们对于 a 序列中元素,在 b 序列中找到它应当对应的元素在 b 序列的位置。也就是对于 a 序列中1,2,3,4…的顺序,到 b 序列中就成了1~n的全排列。于是问题就转化成要将 b 序列的这个排列有序的最少相邻交换次数。
于是我们想到了冒泡排序和逆序对,随便求求逆序对的个数就可以了。采用归并排序完成的方法和数据结构统计的方法都是可以的。
Code:
#include
inline void Rd(temp &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<3)+(res<<1)+(c^48);
while(c=getchar(),c>47);
}
int n,a[M],b[M],p[M],q[M];
long long cnt=0;
bool cmp(int a1,int a2){return b[a1]int p1,int p2){return a[p1]int L,int R){
if(L==R)return;
int mid=L+R>>1;
Merge(L,mid),Merge(mid+1,R);
int low=L,high=mid+1,tot=L;
while(low<=mid&&high<=R)
if(b[low]else{
cnt+=mid-low+1;
p[tot++]=b[high++];
}
while(low<=mid)p[tot++]=b[low++];
while(high<=R)p[tot++]=b[high++];
for(int i=L;i<=R;i++)b[i]=p[i];
}
int main(){
Rd(n);
for(int i=1;i<=n;i++)Rd(a[i]),q[i]=i;
for(int i=1;i<=n;i++)Rd(b[i]),p[i]=i;
sort(q+1,q+n+1,_cmp);
sort(p+1,p+n+1,cmp);
for(int i=1;i<=n;i++)b[p[i]]=q[i];
Merge(1,n);
cnt%=P;
printf("%d\n",(int)cnt);
} 1003. 火车运输
- 并查集+启发式合并
- 生成树+LCA
- 离线+整体二分
现在遇到这种走路径限值的题目就非常害怕。因为标程几乎与Dijkstra那种图论算法根本搭不上边……写这种题目的时候应当将每个点作为集合,或者说集合中的元素来看,然后再采用合并集合的思想进行考虑。
根据本题还要总结一个教训:对于任何图论题,一定要尽可能将其转化为树论题。因为树的性质和可行操作远远比图要多,处在一个图为树的环境下,显然思路会更加广阔。
无论如何,这题都是一道大写的好题。
可能考虑对于每一个询问,我们都跑一遍单源最短路算法,并且要求从经过边权尽可能大的点来转移。在此基础上进行少许优化,期望得分只有30分。
之后由于要求路径上“最小值最大”,于是我们考虑二分的做法。保留所有不小于枚举的最小值的边,再判断需要的路径是否连通即可。复杂度来说,对于 q 个询问,每次都需要 O(logm) 的二分,然后判断图连通需要 O(n) ,最后总时间复杂度为 O(nqlogm) 。显然有待改进。
撇开这种做法不谈,我们可以参照NOIP2012_day2_task2_classroom的二分转线性思路,按边权从大到小枚举这个边权。于是接下来只需要在不断合并的过程中,询问的路径由于边的不断加入而趋向连通。当它第一次连通的时候,加入的边权值就是这个询问的答案了。合并操作我们一般采用并查集去完成。如果判定是否询问的两点连通采用直接for过来的方法,时间复杂度为 O(mq×α(n)) ,期望得分60分。
实际上加入了一条边就是将两个端点所在的集合进行合并,我们可以在进行合并操作的时候顺便处理掉询问,然后再把没有处理掉的两个集合的询问合并起来。显然在极端情况下,如果我们把大集合向小集合进行合并,那么大集合内挂的询问被访问的次数就是 O(m) 的,时间复杂度仍然为 O(mq×α(n)) 。
显然我们可以改变这个合并的顺序,使得每一个询问的访问次数都稳定在 O(logm) 。这就是所谓的启发式合并了,它的操作就只是将小集合向大集合合并,但是这样可以保证每个点被询问到的复杂度在 log 级别。于是时间复杂度就降到 O(qlogm×α(n))≈O(qlogm) 。对于启发式合并的证明和做法亦可以参考题目IOI2011_Race。
/* 启发式合并做法 */
#include if(~ans[now.id])continue;
now.u=getfa(now.u),now.v=getfa(now.v);
if(now.u==now.v)ans[now.id]=dist;
else Mp[v].push_back(now);
}
Mp[u].clear();
}
void solve(){
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u=getfa(Edges[i].u),v=getfa(Edges[i].v);
if(u!=v){
if(Mp[u].size()>Mp[v].size())Merge(v,u,Edges[i].w);
else Merge(u,v,Edges[i].w);
}
}
for(int i=1;i<=q;i++)Pn(ans[i]);
}
int main(){
Rd(n),Rd(m);
for(int i=1,u,v,w;i<=m;i++){
Rd(u),Rd(v),Rd(w);
Edges[i]=(edge){u,v,w};
}
sort(Edges+1,Edges+m+1);
Rd(q);
memset(ans,-1,sizeof(ans));
for(int i=1,u,v;i<=q;i++){
Rd(u),Rd(v);
query now=(query){u,v,i};
Mp[u].push_back(now);
Mp[v].push_back(now);
}
solve();
} 事实上这并不是大众标准解法。
我们接下来是对这些边进行考虑:如果在排除了所有不在同一连通块的询问,那么在统一连通块的询问与加入的边权有什么性质?显然,上述按照边权从大到小加入边的方案,当这部分连通块已经是一棵树的时候,内部的点就已经构成连通了,剩下的边是没有任何用处的。仔细分析这棵树,我们发现它是最大生成树MST(Maximal,滑稽)。于是询问需要在这些最大生成树林上跳跃,所以再套用LCA这个树上的关键点即可,时间复杂度为 O(mlogm×α(n)+(n+q)logn)≈O(mlogm) (sort的锅2333)。
/* 最大生成树做法 */
#include if(now.to!=pre){
dis[now.to]=now.dist;
dfs(now.to,u,d+1,c);
}
}
}
int up(int u,int v){
if(col[u]!=col[v])return -1;
int dist=inf;
while(u!=v){
if(dep[u]return dist;
}
int main(){
Rd(n),Rd(m);
for(int i=1,u,v,w;i<=m;i++){
Rd(u),Rd(v),Rd(w);
Edges[i]=(edge){u,v,w};
}
Kruskal();
for(int i=1;i<=n;i++)
if(!dep[i])dfs(i,0,1,++color);
Rd(q);
for(int i=1,u,v;i<=q;i++)Rd(u),Rd(v),Pn(up(u,v));
} 回到开头那个 O(nqlogm) 的二分。难道本题就真的不能采用二分做法了么?观察这个二分做法,我们发现复杂度堆积在判断边的联通上,显然对于每个询问,都有许多边被重复删除、重构。于是我们考虑在加入边的时候也同时处理掉每个询问,这个做法也就是所谓的在线改离线算法。
对于每一个询问,我们都视作相对独立的一个个小二分块。接下来为了在当前询问前已经合并完所有边权值大于枚举权值的边,我们按照边权值对询问和边混在一起进行排序。遇到边就进行合并,遇到询问就二分,这是非常典型的离线操作的写法。时间复杂度为 O((m+q)logz×α(n)) 。
/* 二分+离线(整体二分)算法 */
#include

1004. 积木大赛
- 暴力模拟
- 贪心
一看到这题,首先想到的是每次暴力找到每一段连续区间内的最小值,然后再减去这个基底,这样就不断劈断区间了。但是考虑到那种一直递增的极端情况,感觉它的时间复杂度是 O(n×h) ,太暴力过不掉。
于是继续考虑那些可以一次就被删除光的区间,最后发现它的性质是不出现 hi−1>hi 且 hi<hi+1 的波谷即可。于是在判断的时候还多判断了上述这一点,结果反而只有80分。最后发现它TM有一段很长的相同高度的“波谷”。所以将上述判定改为 hi−1≥hi 且 hi≤hi+1 就过了。
本题唯一的感觉还是贪心玄学吧。并没有想到 O(n) 的解法。甚至也没有想清这个复杂度并不会像快速排序一样退化得那么严重。但是重点还是在没有进行对拍吧,如果考试的时候试一个“5 3 2 2 4”的数据或许就可以查出来了。只要能拍出一个我就会意识到错误……
本题的暴力做法:
- 每次找到并删去一段连续区间内的最小值,接下来就不断缩小问题规模进行求解。
极限数据是可以卡掉本暴力做法的,只是因为数据比较水40ms都可以过。时间复杂度约为 O(n×h) 。
接下来为了为了进一步优化,我们可以找出那种没有出现“波谷”的情况,即对于这一段区间,无论怎么减去值,都不会劈出新的区间。所以找出“波谷”就可以判掉这种情况。但是这个波谷并不是只有一个点的,它也有可能是一段区间。所以这里处理还会比较麻烦qvq,而且官方数据还会卡这个点。
实际上正解贪心浓缩了上述算法:
- 我们假设每一次搭建操作都是一条删除线,那么答案就是最少的删除线条数。
- 当 hi<hi+1 时,显然必须增加删除线,去补充多出来的 hi+1−hi 部分;
- 当 hi>hi+1 时,有些删除线就必须要终止,接下来只有 hi+1 条删除线可以存在。
于是只需要计算增加的删除线总数即可,时间复杂度为 O(n) 。
Code:
#include
int main(){
int n,pre=0,cnt=0;
scanf("%d",&n);
for(int i=1,val;i<=n;i++){
scanf("%d",&val);
if(pre<val)cnt+=val-pre;
pre=val;
}
printf("%d\n",cnt);
} 1005. 花匠
- 动态规划+数据结构优化
- 贪心
题意其实就是这样一句话:要求构成“波浪形”的序列,求这个最长序列,且这个长度至少为一。那么我们定义 dp[0][i] 表示这个点作为波谷时的最小值, dp[1][i] 对应表示作为波峰的最小值。于是有转移方程式:
我们按照顺序依次处理可以省掉 [1,i) 这一维,接下来再将权值扔进数据结构就可以维护了。如果我们不离散权值,根据NOIP2002_day2_Task2那题的经验,在数据过大的情况下,一定要避免使用线段树。我们发现这个查询是前后缀查询,于是我们可以采用树状数组进行判断,常数会小很多。
正解 O(n) 做法基于贪心中的“回撤”思路:
- 假设当前最优地取到了 g[k] ,并且下一个是波峰,则对于下一个元素 k+1 :
- 若 g[k]<g[k+1] ,说明符合题意,可以继续贪心下去。
- 若 g[k]>g[k+1] ,说明之前若选择 g[k+1] ,则可以取为波峰的情况就更多,于是我们就将最优序列中的 g[k] 替换成 g[k+1] 。
同时根据上述贪心,有以下推论:第一个元素是必须要取的。这也是一种很常见的贪心策略。
- 证明:如果不取第一个元素,就必须有取第k个元素,使得最后得到的解最优(假设下一个要去的元素下标为j)。假设从波谷开始,那么有 g[k]<g[j] :
- 若 g[1]≤g[j] ,则不必考虑从 g[k] 转移,因为 [2,k] 之间可能会产生更多转移;
- 若 g[1]>g[j] ,那么我们就可以从波峰开始,最后结果必然是 g[j] 的最优解 +1 。
同理可证波峰开始的情况。
在缩进了所有相邻元素相同的情况下,不但一定要取最后一个数的贪心可以证明,而且最后的数据整体也就是大波浪形,于是我们在每一个大波浪的谷峰谷底取一下即可。
Code:
#include a[i+1])||
(a[i-1]>a[i]&&a[i]1]);
printf("%d\n",cnt);
} 1006. 华容道
- 广搜 → 最短路
一不小心就敲成dfs了……大概我是受了Spy贪吃蛇那题的刺激,或者没吃早饭饿的眼冒金花的时候一不小心把bfs敲成dfs了吧。qvq
但是如果没有敲dfs我估计也想不到bfs的正解。只可惜暴力的bfs有80分,逼近正解的dfs只有50分,我也是呵呵。以后写图上的搜索题尽量不要写dfs吧,否则今天这一题还是有一搏之力的……
基础搜索算法的选择:深搜dfs or 广搜bfs?
- 如果这道题目两者方法都通用倒是没什么关系……但是如果作者设计的时候就已经尽可能减少了某一种搜索的剪枝,那没改回来就会浪费起码半小时了……
- 这道题目采用bfs的理由是:
- bfs的实现更加简单,并且在时间系数上要比dfs小(当然需要手写队列实现)(大神才会用dfs魔性剪枝,蒟蒻还是乖乖敲简单的bfs就好了)。
- 本题除了dis值以外,我们只需要存储空白点和目标移动点的坐标。显然本题有非常多的重复情况,用bfs在判重上更为方便。(dfs在判重方面简直NPC)
判重部分
- 注意本题的状态只有两个点的坐标,且坐标范围都很小。对于所有判重方案(mark,Hash+map,set)中,我们可以直接采用四维的mark数组进行标记。这样判重就不带复杂度了。
- 判断是否到达最终位置的时候不要在扩展节点后再判断,因为bfs的性质,向外扩展更新的时候已经是目前最优解了。那么当它扩展到最终位置后必然最优。充分利用bfs的最优性(相对的,dfs则是保证字典序一定最优)。
算法实现的不同
- 此处思路可以参见国家集训队2008论文集_肖汉骏例题2-2,与本题华容道是一样的。
- 我们如果以空白点作为基准,搜索它的移动,那么就是标准的暴力bfs,只需要判断空白点下一步是否为目标点即可。期望得分80分。
- 如果我们以目标节点作为基准,搜索它的移动,那么就会发现性质:首先根据华容道游戏本身的性质,当起始棋子开始移动后,空白点与它相邻;其次,在起始棋子开始移动后,在它接下来的移动中,四周空白点如何实现这一移动的次数是固定的。根据上述性质,我们将这个实现次数转化成边权起始棋子移动的边权。因为边权不为1不能跑bfs,所以我们跑最短路。
四周空白点处理的时候,我的处理方法是:保存空白点坐标+起始棋子的相对方向+目标位置相对于起始棋子的方向的四维组。
代码一交,发现WA在大数据上。后来灵光一现觉得可能是溢出的问题,接着也发现是溢出在预处理的地方,于是改大一点范围就过了。
讲真代码实现的比较恶心,mark数组和Dijkstra部分还能再优化的。但是再调下去我就是只废铅了qvq。
Code:
#include return false;
a=b;return true;
}
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};
#define fi first
#define se second
//-----------------------------
typedef pair<int,int> pii;
pii goal;
int pic[N][N],n,m,kase;
bool judge(int x,int y){
return x<=n&&x&&y<=m&&y&&pic[x][y];
}
bool mark[N][N][N][N];
int dp[N][N][4][4];
struct node{
int x1,y1;//起始棋子位置
int x2,y2;//空白点的位置
int dis;
bool operator < (const node &cmp)const{
return dis>cmp.dis;
}
};
//-----------------------------
int dist[N][N];
int direction(int x1,int y1,int x2,int y2){//node1->node2
//node 2 相对于node 1所在位置
int xd=x2-x1,yd=y2-y1;
int d;
for(d=0;d<4;d++)
if(dx[d]==xd&&dy[d]==yd)return d;
assert(d<4);
}
pii que[M];
void bfs(node st){//先让白色棋子与起始棋子相邻(白色棋子走向起始棋子)
pic[st.x1][st.y1]=0;
clear(dist,-1);
dist[st.x2][st.y2]=0;
int L=0,R=-1;
que[++R]=pii(st.x2,st.y2);
while(L<=R){
pii now=que[L++];
for(int d=0;d<4;d++){
pii nxt=pii(now.fi+dx[d],now.se+dy[d]);
if(!judge(nxt.fi,nxt.se)||~dist[nxt.fi][nxt.se])continue;
dist[nxt.fi][nxt.se]=dist[now.fi][now.se]+1;
que[++R]=nxt;
}
}
pic[st.x1][st.y1]=1;
}
void init(){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)//枚举blank点
if(pic[i][j])for(int d=0;d<4;d++){//枚举起始棋子点
pii nxt=pii(i+dx[d],j+dy[d]);
if(!judge(nxt.fi,nxt.se))continue;
bfs((node){nxt.fi,nxt.se,i,j,0});
for(int k=0;k<4;k++)//枚举下一个转移点
if(!~dist[nxt.fi+dx[k]][nxt.se+dy[k]])dp[i][j][d][k]=-1;
else dp[i][j][d][k]=dist[nxt.fi+dx[k]][nxt.se+dy[k]]+1;
}
}
int Dijkstra(node st){
if(st.x1==goal.fi&&st.y1==goal.se)return st.dis;
priority_queueq;
bfs(st);
for(int d=0;d<4;d++){
int x=st.x1+dx[d],y=st.y1+dy[d];
if(~dist[x][y])q.push((node){st.x1,st.y1,x,y,dist[x][y]});
}
while(!q.empty()){
node now=q.top();q.pop();
if(now.x1==goal.fi&&now.y1==goal.se)return now.dis;
if(mark[now.x1][now.y1][now.x2][now.y2])continue;
mark[now.x1][now.y1][now.x2][now.y2]=true;
int k=direction(now.x2,now.y2,now.x1,now.y1);
for(int d=0;d<4;d++){
int x=now.x1+dx[d],y=now.y1+dy[d];
assert(d==direction(now.x1,now.y1,x,y));
if(!judge(x,y)||!~dp[now.x2][now.y2][k][d])continue;
q.push((node){x,y,now.x1,now.y1,now.dis+dp[now.x2][now.y2][k][d]});
}
}return -1;
}
int main(){
Rd(n),Rd(m),Rd(kase);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)Rd(pic[i][j]);
clear(dp,-1);
init();
while(kase--){
clear(mark,0);
node st;
Rd(st.x2),Rd(st.y2),Rd(st.x1),Rd(st.y1);st.dis=0;
Rd(goal.fi),Rd(goal.se);
printf("%d\n",Dijkstra(st));
}
}