数据结构之哈弗曼编码的（Huffman Coding）加密解密压缩

　　Huffman树又叫最优二叉树，它的特点是带权路径最短。
　　Huffman树的一个重要应用是Huffman编码，Huffman编码是长度最短的前缀编码。即给定要传送的字符的权值，根据权值求出Huffman编码，它一定是前缀编码（指任意字符的编码都不是另一个字符编码的前缀），并且在传送过程由字符组成的文字时，编码长度最小。
　　因此Huffman编码可以对文字进行加密解密还有压缩。加密的工作就是将文字转换为编码，解密工作是将编码转换为文字，如何转换本文不做详解（严蔚敏的《数据结构》书中有代码）。那么如何进行压缩？当字符转变为编码，如果数字编码用char数组存储，则size并未减少。因此我们考虑用位操作。
　　由于编码完成后，码的形式是0和1组成的串，因此按位存储比原来将节省空间，假设平均编码长度为5位(若平均编码长度超过8位则没有压缩效果了，毕竟char是一个字节，但不可能超过8位，因为根据Huffman编码性质编码长的出现频率低，编码短的出现频率高，后面结果也得到了验证)，则64位8个字节可以存储12.8个字符，而char只能存储8个字符。因此文字得到了压缩。
　　整个程序执行过程如图所示：
　　
　　其中最难的是writeFile，利用位操作将编码组合在一起并写入文件，这里我们定义一个Unit单元，它包含64位数据，每次编码塞满64位数据，则写入文件。
　　按照上面的思想，写成的代码如下：

// HuffmanCode.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef unsigned __int64 Dcode;
//Aesop_Fables.txt  graph.txt
char *readFileName = "graph.txt";  //读的文件名称
char *writeFileName = "graph_compress.dat";  //写的文件名称

typedef struct  HCBinary
{
    Dcode binaryCode;  //哈弗曼编码的二进制表示方法
    int length;  //编码长度
}HCBinary;


typedef struct Unit
{
    Dcode content;
    int remain;
}Unit;

Unit tempUnit;

typedef struct
{
    long long int weight;
    int parent, lchild, rchild;
    char ch;
}HTNode, *HuffmanTree;

map<char, long long int> frequencyMap;
map<char, HCBinary> codeMap;

void select(HuffmanTree &HT, int dest, int &s1, int &s2)//选择两个最小的元素，获得它们的位置
{
    long long int min1 = 9999999999;   //先让min1，min2为一个足够大的数
    long long int min2 = 9999999999;
    int tempS1 = 0;    //用来记录位置
    int tempS2 = 0;
    for (int i = 1; i <= dest; i++)
    {
        if (HT[i].parent != 0)   //说明已经被用过，则直接跳到下一个
        {
            continue;
        }
        else
        {
            if (HT[i].weight <= min2)
            {
                if (HT[i].weight <= min1)
                {
                    min2 = min1;
                    tempS2 = tempS1;
                    min1 = HT[i].weight;
                    tempS1 = i;
                }
                else
                {
                    min2 = HT[i].weight;
                    tempS2 = i;
                }
            }
        }
    }
    s1 = tempS1;
    s2 = tempS2;
}

int select2(HuffmanTree &HT, int dest)
{
    long long int min = 9999999999;
    int pos=0;
    for (int i = 1; i <= dest; i++)
    {
        if (HT[i].parent != 0)   //说明已经被用过，则直接跳到下一个
        {
            continue;
        }
        else if(HT[i].weight < min)
        {
            min = HT[i].weight;
            pos = i;
        }
    }
    return pos;
}

void HuffmanCoding(HuffmanTree &HT, char** &HC)  //哈弗曼编码，其实就是填表的过程
{
    int c, f, m, i;
    int start;
    int s1, s2;
    HuffmanTree p;
    char * cd;
    int n = frequencyMap.size();
    if (n <= 1)
    {
        exit(0);
    }
    m = 2 * n - 1;    //根据哈弗曼树的性质，可得总结点数m=2n-1
    HT = new HTNode[m + 1];   //0号元素不用
    map<char, long long int>::iterator iter = frequencyMap.begin();
    for (p = HT + 1, i = 1; i <= n; i++, ++p) //先初始化所有叶子节点
    {
        p->ch = iter->first;
        p->weight = iter->second;   //由于0号元素是不用的所以要加1
        p->lchild = 0;
        p->rchild = 0;
        p->parent = 0;
        iter++;
    }
    for (; i <= m; ++i, ++p)   //初始化其他节点
    {
        p->ch = NULL;
        p->weight = 0;
        p->lchild = 0;
        p->rchild = 0;
        p->parent = 0;
    }
    for (i = n + 1; i <= m; ++i)
    {
        select(HT, i - 1, s2, s1);  //选择两个最小的元素，获得它们的位置
        /*s1 = select2(HT, i - 1);
        s2 = select2(HT, i - 1);*/
        HT[s1].parent = i;
        HT[s2].parent = i;
        HT[i].lchild = s1;
        HT[i].rchild = s2;
        HT[i].weight = HT[s1].weight + HT[s2].weight;
    }
    HC = new char*[n + 1];
    cd = new char[n];
    cd[n - 1] = '\0';
    for (i = 1; i <= n; ++i)
    {
        start = n - 1;
        for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
        {
            if (HT[f].lchild == c)
                cd[--start] = '0';
            else
                cd[--start] = '1';
        }
        HC[i] = new char[n - start];
        strcpy_s(HC[i], n - start, &cd[start]);
    }
    delete cd;
}

void getBinaryCode(char** HC)   //获取56种哈弗曼编码的二进制，存储在code中
{
    int i;
    int j;
    Dcode ZERO = 0;
    Dcode ONE = 1;
    map<char, long long int>::iterator iter = frequencyMap.begin();
    HCBinary tmpCode;
    for (i = 1; i <= frequencyMap.size(); i++)
    {
        tmpCode.binaryCode = 0;
        tmpCode.length = 0;
        for (j = 0; HC[i][j] != '\0'; j++)
        {
            if (HC[i][j] == '1')
            {
                tmpCode.binaryCode <<= 1;                      //必须要先移动再或
                tmpCode.binaryCode = ONE | tmpCode.binaryCode;

            }
            if (HC[i][j] == '0')
            {
                tmpCode.binaryCode <<= 1;
            }
            tmpCode.length++;
        }
        codeMap[iter->first] = tmpCode;
        iter++;
    }
}

void init()  //初始化
{
    tempUnit.content = 0;
    tempUnit.remain = 64;
}

void computeFrequent()  //计算字符出现的频率
{
    int i;
    fstream fp(readFileName, ios::in);
    if (!fp)
    {
        cout << "can't open the file." << endl;
        exit(0);
    }
    char ch;
    while (ch = fp.get(), !fp.eof())
    {
        frequencyMap[ch] += 1;
    }
    fp.close();
}


void writeFile()
{
    int i;
    fstream readFp(readFileName, ios::in);
    fstream writeFp(writeFileName, ios::out | ios::binary);
    if (!readFp || !writeFp)
    {
        cout << "can not open the file!" << endl;
        exit(0);
    }
    char ch;
    HCBinary tempCode;
    while (ch = readFp.get(), !readFp.eof())
    {
        tempCode = codeMap[ch];
        if (tempUnit.remain == tempCode.length)  //若单元中剩余位置大小等于code长度
        {
            tempUnit.content <<= tempCode.length;
            tempUnit.content |= tempCode.binaryCode;
            writeFp.write((char*)(&tempUnit.content), sizeof(tempUnit.content));  //将单元整个写入

            tempUnit.remain = 64;         //初始化该单元
            tempUnit.content = 0;

        }
        else if (tempUnit.remain>tempCode.length)  //若单元中剩余位置大小大于code长度，将code放入单元中
        {
            tempUnit.content <<= tempCode.length;
            tempUnit.content |= tempCode.binaryCode;
            tempUnit.remain = tempUnit.remain - tempCode.length;
        }
        else    //若单元中剩余位置大小小于code长度，将部分code放入单元，则要先将部分code写入单元，在将单元写入文件后，将其余code写入单元
        {
            Dcode temp = 0;
            tempUnit.content <<= tempUnit.remain;
            temp = tempCode.binaryCode >> (tempCode.length - tempUnit.remain);
            tempUnit.content |= temp;
            writeFp.write((char*)(&tempUnit.content), sizeof(tempUnit.content));

            tempUnit.content = 0;
            temp = 0xFFFFFFFFFFFFFFFF;  //不用数了，16个F
            temp <<= (tempCode.length - tempUnit.remain);
            temp = ~temp;//求反
            temp &= tempCode.binaryCode;
            tempUnit.content |= temp;
            tempUnit.remain = 64 - (tempCode.length - tempUnit.remain);
        }
    }
    if (tempUnit.remain != 64)   //说明，还有一个单元没有被写入，将剩余的写入
    {
        //FIXME:这样会导致多写入0，那么如果有哈弗曼编码位00..,就会出错
        tempUnit.content <<= tempUnit.remain;
        writeFp.write((char*)(&tempUnit.content), sizeof(tempUnit.content));
    }
    readFp.close();
    writeFp.close();
}

void Decode(HuffmanTree &HT)  //解码过程
{
    int len = frequencyMap.size();
    int f = 2 * len - 1;
    int c = 0;
    int i;
    fstream readFp(writeFileName, ios::in | ios::binary);
    if (!readFp)
    {
        cout << "can not open the file." << endl;
        exit(0);
    }
    Dcode one = 0;
    Dcode temp = 0;
    Dcode temp2 = 0;
    one = 0x8000000000000000;
    while (!readFp.eof())
    {
        readFp.read((char*)(&temp2), sizeof(Dcode));
        if (readFp.fail())
        {
            break;
        }
        for (i = 0; i<64; i++)     //根据得到的0,1从根节点往下，直到叶子节点输出相应字符
        {
            temp = temp2&one;
            if (temp == 0)
            {
                c = HT[f].lchild;
            }
            else
            {
                c = HT[f].rchild;
            }
            f = c;
            temp2 <<= 1;
            if (HT[c].lchild == 0 && HT[c].rchild == 0)
            {
                cout << HT[c].ch;
                f = 2 * len - 1;
                c = 0;
            }
        }
    }
    readFp.close();
}

int main()
{
    init();
    computeFrequent();
    HuffmanTree HT;
    char** HC;
    HuffmanCoding(HT, HC);
    cout << "字符" << setw(20) << "出现频率" << setw(25) << "哈弗曼编码" << endl;
    map<char, long long int>::iterator iter = frequencyMap.begin();
    for (int i = 1; i <= frequencyMap.size(); i++)
    {
        cout << iter->first << setw(20) << iter->second << setw(25) << HC[i] << endl;
        iter++;
    }
    getBinaryCode(HC);
    writeFile();
    cout << "压缩完成" << endl;

    cout << "开始解码：" << endl;
    Decode(HT);
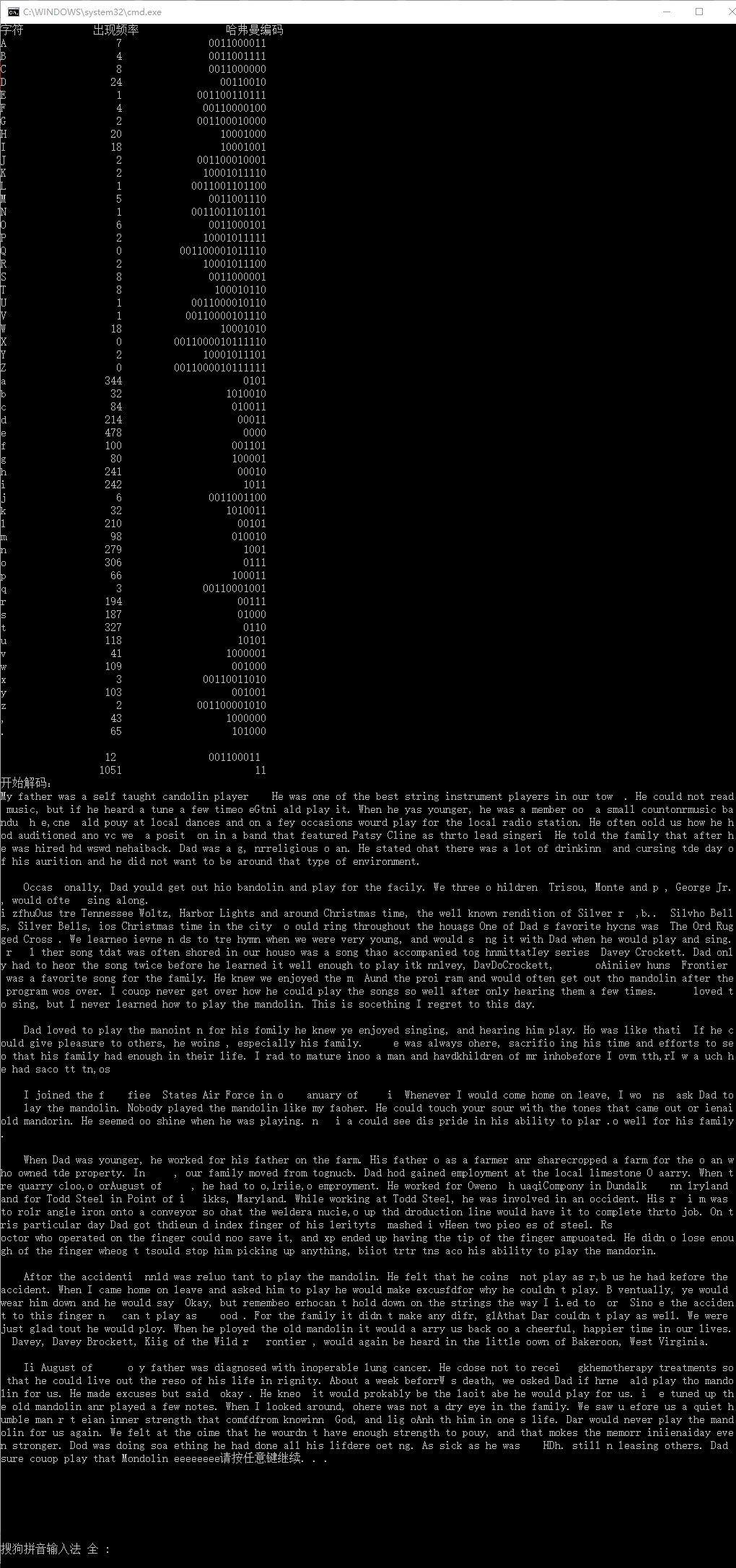
    return 0;
}

　　程序的执行结果如下图：
　　
　　
　　可以看到整篇文章的确进行了压缩（从6KB->3KB）。这里出现了一个小问题，最后多输出了eeeeeeee。由于我们是以64位为一个单元进行写入的，当最后一个单元不满64时，我们以0进行填充，而e的编码为0000，所以最后一个单元剩余的内容都被解析成了e。
　　解决方法可以在增加一个字符“截止符”，并和其他字符一起计算Huffman码，当写完最后一个单元的时候将截止符也写入，解码过程中若碰到“截止符”则跳出函数，不再解码。