单调栈、单调队列、线段树、LCA、二维树状数组、Bitset讲解
一、单调栈
1.问题引入
考虑这样一个问题,给出一个数字序列,一段连续的子序列的权值定义为这个子序列中最小的权值乘以子序列的长度,求最大的子序列权值,数据范围O(n)可过。
2.问题转化
稍加思索我们可以得到一个O(n^2)的算法,但是显然是太慢,我们想办法换一种枚举方式,假如我们枚举每一个数作为最小值,计算这个序列最大能扩张多长,那么这样就优化成了O(n)个数进行比较,于是只要能快速算出一个数作为最小的数最多能向左向右扩张多少就可以了,这里我们开始介绍单调栈算法。
3.单调栈
顾名思义,单调栈,首先是一个栈,且栈内元素有单调性,单调栈的维护也很简单,只要在加入元素的时候暴力弹栈维护单调性即可。
下面为了让大家理解,我模拟一下单调栈的过程。
这是一个数字序列
1 6 4 8 9 2 3
我们开始模拟一个单调递增单调栈的过程
加入1:1
加入6:1 6
加入4:1 4(弹掉6)
加入8:1 4 8
加入9:1 4 8 9
加入2:1 2(弹掉4 8 9)
加入3:1 2 3
由于每个元素至多进栈一次出栈一次,所以总时间复杂度是O(n)的。
那我们开始看单调栈如何优化上面的问题吧
我们首先观察到当后面的数弹掉前面的数的时候后面的数也一定是前面的数向右扩张时碰到的第一堵“墙”,那么在弹掉元素的时候我们就可以更新一下被弹掉数向右扩张的边界,最后栈内剩下的的数向右扩张不会遇到障碍,所以剩下的元素都可以扩张到最后的位置。
那么向左扩张的边界呢?有两种解决办法,一种就是将这个数组反过来做一遍,简单易懂。另一种就是我们观察这个单调栈,每次加入元素之后其左面的数也一定是第一个比它小的数,所以在将元素入栈的时候即可更新其向左扩张的边界。
由于只用到了单调栈,所以算一个数向左向右的边界时间复杂度就优化成了O(n),最后对每一个数计算一下答案,总时间复杂度也是O(n)。
4.单调栈能解决什么问题?
好像就能解决上面的问题QAQ
例题:
bzoj1660

题目解析:
很明显的一个思路,我们可以算出每一头牛右面第一个比它高的牛在哪里,然后答案加上see[i]-i即可,还有另一种算法更为简单,我们可以换一个考虑角度,计算每一头牛能被多少头牛看到,那么我们维护一个单调递减的单调栈,加入元素时弹完栈后栈内元素个数即为这头牛可以被多少头牛看到。
代码:
#includereturn 0;
} 二、单调队列
1.单调队列
有了单调栈,单调队列就不用铺垫了,单调队列与单调栈唯一的区别也就是队列与栈的区别,单调队列只要维护一个首指针支持前端删除就行了。
2.单调队列的应用
(1).得到每一个连续长度为k区间的最大(最小)值
单调队列的基础应用,例如我们要求最大值我们只要维护一个单调递减的队列,当队首的下标与新加入元素的下标差超过K就弹掉队首即可。
(2).优化DP
假设有这么一个DP: F[i]=(max F[j]+…),i−j≤k ,我们就可以用上面的原理来优化这个DP。
(3).其它应用
本质上都是第一个应用的扩展。
例题
http://caioj.cn/problem.php?id=1173
代码
#includeq[t-1]]) t--;
q[t++]=i;
}
cout<return 0;
} 三、线段树
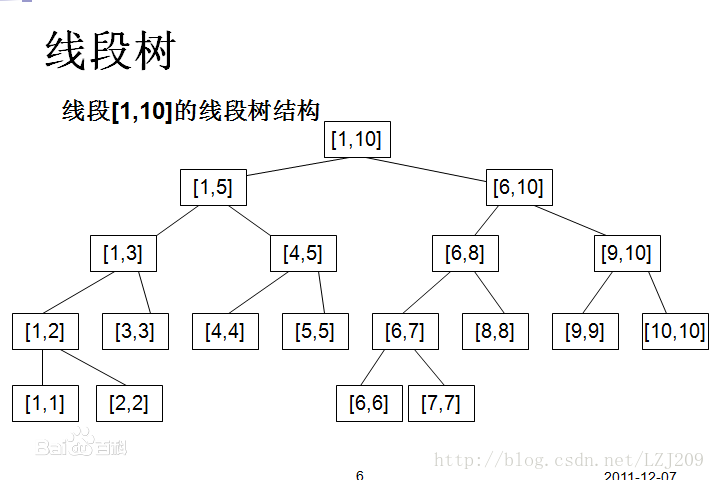
1.什么是线段树
2.线段树的写法
首先线段树会有左右儿子,用数组的话很方便的一个做法就是o节点的左儿子为2*o,o节点的右儿子为2*o+1,我们可以开一个结构体存每一个节点的信息,需要维护什么就维护什么。
3.模板例题
给出一个序列,查询[x,y]的最大值。
代码:
#includer) return -2147483647;
if(a[o].l>=l && a[o].r<=r) return a[o].maxx;
return max(query(2*o,l,r),query(2*o+1,l,r));
} 就是给大家看看板子QAQ
4.标记
当我们进行单点修改的时候显然可以直接找到叶子节点进行修改然后在回溯的过程中更新节点信息,但是当我们进行区间修改的时候我们就需要一个新的帮手:懒标记。
当我们修改一段区间的时候,在线段树上找到对应的若干个小区间,对每一个区间打上一个标记,当再次修改或者查询的时自上向下将标记推下去,实现区间修改O(logn),这个相信大家都有听过,这里不再赘述,如果有不会的同学,在课下问我。
5.标记永久化
这个在普通线段树中一般用处不大,但是也有这样的题,标记永久化在二维线段树中就尤为重要,有些标记是可以永久化的,就比如说加标记,所谓标记永久化,就是在修改的时候在对应节点上加上这么一个标记,然后此标记不下推,但是要更新父亲节点的信息,在查询一个节点的权值时候从上到下加起来每一个父亲节点的标记,从而推出该节点正确的权值。
6.常见标记
赋值标记、加标记、乘标记、等差数列标记、翻转标记(01翻转,左右翻转)
7.线段树分治
当我们有n个物品,要求不使用某个物品用剩下的物品所能组合成的balabala时,就可以使用线段树分治,具体实现就是往左儿子走就将右儿子代表的物品全加进去,往右儿子走就把做儿子代表的物品全加进去,最后遍历到每一个叶子就是不选这个物品的方案,每个物品会被加入logn次,线段树的节点个数是O(n)级别,所以总时间复杂度就是nlogn.
(这个我可能写的不清楚,听我讲吧QAQ
例题:
BZOJ1699线段树裸题,练板子
BZOJ1798
老师交给小可可一个维护数列的任务,现在小可可希望你来帮他完成。 有长为N的数列,不妨设为a1,a2,…,aN 。有如下三种操作形式: (1)把数列中的一段数全部乘一个值; (2)把数列中的一段数全部加一个值; (3)询问数列中的一段数的和,由于答案可能很大,你只需输出这个数模P的值。
解析:
线段树懒标记裸题,记得在推乘标记的时候要把加标记也乘上乘标记,而且要先推乘标记,再推加标记。
GSS系列题
BZOJ3211
BZOJ1018
BZOJ4653
TYVJ4751(http://www.tyvj.cn/p/4751)
四、LCA
1.前言
LCA是算法竞赛中树上问题很重要的部分,掌握LCA基本上算是学会树上问题的第一步
2.LCA的主要算法
(1).倍增法
预处理出每个点向上爬2^i的祖先是谁,先让深度深的点爬到和深度浅的点同一高度,然后两个点同时向上爬,直到两个点爬到LCA,因为我们预处理出了2^i的祖先,所以向上爬的过程可以优化成O(logn)的,预处理时间复杂度O(nlogn),单次查询LCA时间复杂度O(logn)
int deep[200000];
int fa[200000][18];
void dfs(int u,int fro)
{
deep[u]=deep[fro]+1;
fa[u][0]=fro;
for(int o=fir[u];o;o=nex[o]) if(a[o].r!=fro) dfs(a[o].r,u);
}
void init()
{
dfs(1,0);
for(int i=1;i<=17;i++)
for(int j=1;j<=200000;j++) fa[j][i]=fa[fa[j][i-1]][i-1];
}
int lca(int x,int y)
{
if(deep[x]for(int i=17;i>=0;i--) if(deep[fa[x][i]]>=deep[y]) x=fa[x][i];
if(x==y) return x;
for(int i=17;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
return fa[x][0];
} (2).ST表
首先我们引入欧拉遍历序,首先我们来区分一下欧拉遍历序和入栈出栈序。
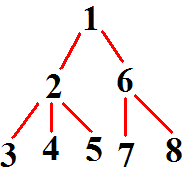
这颗树的入栈出栈序为:1 2 3 3 4 4 5 5 2 6 7 7 8 8 6 1
这棵树的欧拉遍历序为:1 2 3 2 4 2 5 2 1 6 7 6 8 6 1
可以很清楚地看出两种序列的不同之处。
对于入栈出栈序我们在dfs的时候每个点入栈时加入一遍出栈时加入一边,总点数显然是2*n的。
对于欧拉遍历序我们则是完全模拟dfs的过程,到一个点加入一个点,由于每条边会被走两遍,再加上第一个点,总点数为2*n-1。
这两种遍历序各有各的优势,但是在求LCA的时候我们要用到的是欧拉遍历序,不难看出,我们要是想求两个点的LCA,只要随便在欧拉遍历序上找到这两个点(相同的任取一个),两个点之间深度最浅的一定是两个点的LCA,维护一段序列的最小值,我们显然可以用线段树,但是线段树常数又大又不好写,所以这里我推荐大家写ST表,首先时间复杂度优越,而且常数小,当询问LCA次数特别多时ST表有巨大的优势。
我们预处理出一个点向后扩张2^i格深度最小值是多少以及是哪个点,这样在求两个点之的LCA时只要这么一步: LCA=deep[minn[i][j]]<deep[minn[i−(1<<j)+1][j]]?minn[i][j]:minn[i−(1<<j)+1][j]
这样的话预处理时间复杂度是O(nlogn)的,单次求LCA时间复杂度为O(1)
(3).树链剖分
这个后天有人会讲,今天我就不再赘述,但是我可以先告诉大家树链剖分的预处理时间复杂度为O(n),单次询问为O(logn)而且这个logn很难跑满,是所有单次查询O(logn)的算法中均摊效果最好的一种算法。
(4).随机数据
如果一颗树是随机的,那么这棵树期望是logn层的,找lca暴力就可以了。。
3.总结
LCA的算法很多,但我觉得这三种就已经够用了,倍增的优势是方便实现,ST表适合处理询问LCA次数特别多的题目,而树剖则是一个常数很小1的算法,适合询问LCA次数较少的题目,大家具体问题具体分析。
例题
NOIP2013货车运输
https://www.luogu.org/problem/show?pid=1967
五、二维树状数组
1.树状数组
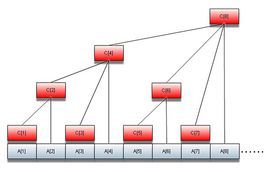
这就是树状数组的结构,每一个数加上它的lowbit值对应的节点就是它在树状数组中的父亲,它可以实现区间加减单点求值,也可以实现单点修改区间查值,其他操作则需要一点转化,由于我们这里主要讲二维的树状数组,所以这里不再赘述。
2.如何理解二维数据结构
二维数据结构的特点是每一个二维节点中都包含着一个一维的数据结构,而二维数据结构中的一维数据结构则是该二维数据结构所包含的一位数据结构信息的整合,我知道这样说会比较绕,所以我们来举一个栗子。
我们用二维线段树来理解二维数据结构(二维线段树只是好理解,但是很难写)
(这个没有办法用文字来写,我现场讲)
3.二维树状数组和一维树状数组的区别
没啥区别,除了多写一维,注意下标也要从1开始
代码
//在点x,y上加一个v
void add(int x,int y,int v)
{
for(int i=x;i<=n;i+=i&(-i))
for(int j=y;j<=n;j+=j&(-j))
c[i][j]+=v;
}
//查询以(1,1)为左下角,(x,y)为右上角的子矩形的权值和
int get_val(int x,int y)
{
int re=0;
for(int i=x;i;i-=i&(-i))
for(int j=y;j;j-=j&(-j))
re+=c[i][j]
return re;
}六、Bitset
(前天YihAN_Z讲STL的时候忘了讲了,今天我来填上这个坑
当我们需要二进制运算的时候,每一个二进制位都存在一个int里显然太慢了,我们考虑到int是32位的,那么我们就可以将30位二进制压成一个int,这样总的时间复杂度就可以除以一个32,(一般100000的数据常数小的话,n^2/32是没有什么压力的)
但是这个东西手写还是太麻烦了,C++就非常人性的给大家提供了一个非常厉害的工具:Bitset。
Bitset怎么用呢,请大家打开今天下发的C-free,然后听我讲。
bitset的应用
正常如果有一种运算只涉及01并且性质和左移右移与或非相近,那么我们就可以使用bitset来优化这个运算。
例题
BZOJ3687