Sift特征详解

摘自—here—- and here
高斯模糊

1.概述

全称：Scale Invariant Feature Transform（尺度不变特征变换）
对旋转，尺度缩放，亮度变化等保持不变性，是一种非常稳定的局部特征。

1.1 sift算法具有的特点

1.图像的局部特征，对旋转，尺度缩放，亮度变化保持不变，对视角变化，仿射变换，噪声也保持一定程度的稳定性。
2.独特性好，信息量丰富，适用于海量特征库进行快速、准确的匹配；
3.多量性，即使是很少的几个物体也可以产生大量的sift特征；
4.高速性，经优化的sift匹配算法甚至可以达到实时性
5.扩招性，可以很方便的与其他的特征向量进行联合

1.2 特征检测的步骤——4步

1.尺度空间的极值检测：搜索所有尺度空间上的图像，通过高斯微分函数来识别潜在的对尺度和选择不变的兴趣点。
2.特征点定位：在每个候选的位置上，通过一个拟合精细模型来确定位置尺度，关键点的选取依据他们的稳定程度；
3.特征方向赋值：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向，后续的所有操作都是对于关键点的方向，尺度和位置进行变换，从而提供这些特征的不变性。
4.特征点描述：在每个特征点周围的邻域内，在选定的尺度上测量图像的局部梯度，这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变换。

2.尺度空间

参考
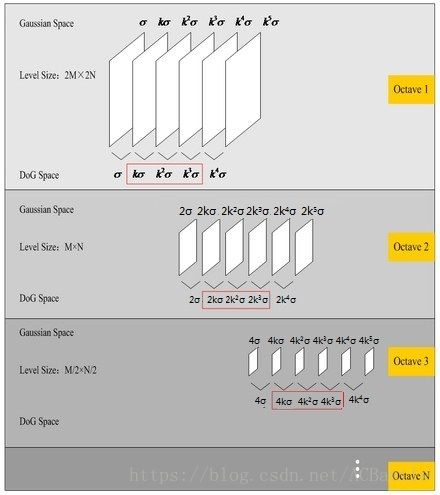
2kσ中的2是必须的，尺度空间是连续的，将第0层的初始尺度定为1.6，图片的初始尺度定为0.5（最清晰）,在检测极值点前对原始图像的高斯平滑以致图像丢失高频信息，所以Lowe建议在建立尺度空间前首先对原始图像长宽扩展一倍，以保留原始图像信息，增加特征点数量，尺度越大图像越模糊。

算法描述

1.构建尺度空间

这是初始化操作：尺度空间理论目的是模拟图像数据的多尺度特征
高斯卷积核是实现尺度变换的唯一线性核，于是二维图像的尺度空间定义为：

L(x,y,σ)=G(x,y,σ)∗I(x,y) L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y )

G(x,y,σ)=12\PIσ2e−(x2+y2)/2σ2 G ( x , y , σ ) = 1 2 \PI σ 2 e − ( x 2 + y 2 ) / 2 σ 2

其中 G(x,y,σ) G ( x , y , σ ) 是尺度可变高斯函数：
（x,y）是空间坐标，是尺度坐标，σ大小决定图像的平滑程度，大尺度对应图像的概貌特征，小尺度对应图像的细节特征。大的σ值对应粗糙尺度(低分辨率)，反之，对应精细尺度(高分辨率)。为了有效的在尺度空间检测到稳定的关键点，提出了 高斯差分尺度空间（DOG scale-space = Difference of Gaussian scale-space）。利用不同尺度的高斯差分核与图像卷积生成。

D(x,y,σ)=（G(x,y,kσ)−G(x,y,σ))∗I(x,y)=L(x,y,kσ)−L(x,y,σ) D ( x , y , σ ) = （ G ( x , y , k σ ) − G ( x , y , σ ) ) ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ )

图像金字塔的建立， 后面每个octave为上一个octave降采样的结果，即原图的1/4（长宽各减半）

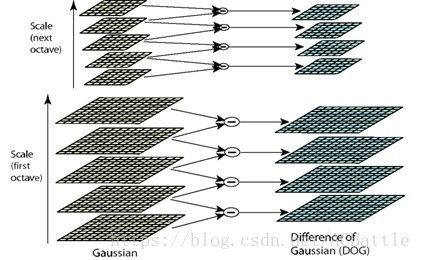
2i−1(σ，kσ，k2σ,...,kn−1σ),k=21/s 2 i − 1 ( σ ， k σ ， k 2 σ , . . . , k n − 1 σ ) , k = 2 1 / s i为octave的塔数，s为每塔层数

2.Log近似Dog找到关键点<检测DOG尺度空间极值点>

为了寻找尺度空间的极值点，每一个采样点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小，如图所示，中间的检测点和它同尺度的8个相邻点和上下尺度对应的9×2个点，共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。一个点如果在DOG尺度空间本层以及上下两层的26个邻域中是最大或者最小值时，就认为该点是图像在该尺度下的一个特征点。


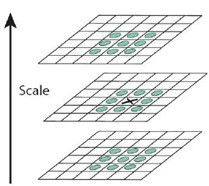
在极值的比较过程中，每一组图像的首末两层是无法进行极值比较的，为了满足尺度变化的连续性，为了每组检测s个尺度的极值点，则DOG金字塔有S+2层图像（因为是相邻的两个很找极值点），所以高斯金字塔有每组s+3层图像（为了生成s+2个DOG金字塔）。

3.除去不好的特征点

这一步本质上要去掉DOG局部曲率非常不对称的像素。(不懂)
以上检测到的极值点是离散空间的极值点，需要我们通过拟合三维二次函数来精确确定关键点的位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点（因为DOG算子会产生较强的边缘相应），以提高抗噪声能力。
3.1 精确定位

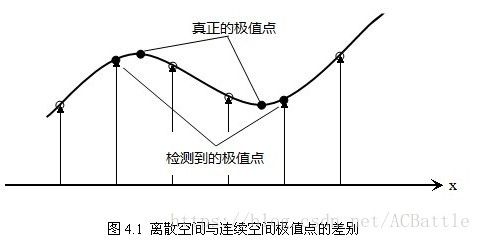
离散空间的极值点并不是真正的极值点（上图可看出，并不一致）
利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值（Sub-pixel Interpolation）。
为了提高关键点的稳定性，需要对尺度空间DoG函数进行曲线拟合。
3.2消除边缘响应
一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。DOG算子会产生较强的边缘响应，需要剔除不稳定的边缘响应点。获取特征点处的Hessian矩阵，主曲率通过一个2x2 的Hessian矩阵H求出。

4.给特征点赋值一个128维方向参数

上一步中确定了每幅图中的特征点，为每个特征点计算一个方向，依照这个方向做进一步的计算，利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性。

m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2

θ(x,y)=atan2(L(x+1,y)−L(x−1,y))/(L(x,y+1)−L(x,y−1)) θ ( x , y ) = a t a n 2 ( L ( x + 1 , y ) − L ( x − 1 , y ) ) / ( L ( x , y + 1 ) − L ( x , y − 1 ) )

为（x,y）处梯度的模值和方向公式，其中L所用的尺度为每个关键点各自所在的尺度。至此，图像的关键点已经检测完毕，每个关键点有三个信息： 位置，所处尺度，方向，可以确定一个sift特征区域。
梯度直方图的范围是0~360，其中每10个度一个柱，总共36个柱。

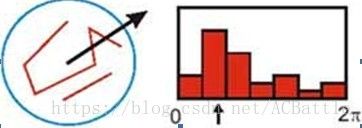
Lowe指出使用高斯函数对直方图进行平滑，减少突变的影响 直方图的峰值代表了该关键点处邻域梯度的主方向，即作为该关键点的方向

通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。

5.关键点描述子的生成

接下来就是为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

利用公式求得每个像素的梯度幅值与梯度方向，然后用gaussian窗口(不懂)对其进行加权运算。

6.根据sift进行Match