MATLAB通信系统建模与仿真
第二部分:随机信号分析
1.平稳随机过程的自相关函数和功率谱密度
例.产生100个N=2000的独立同分布的均值为0,方差为1的高斯分布随机的离散时间序列,计算序列的自相关估值和功率谱密度的平均值。
程序如下:
clear all
N1=2000;
N2=100;
x=randn(N2,N1); %生成N2行N1列,每一行表示一个序列
for ii=1:N2
[Rx(ii,:),lags]=xcorr(x(ii,:),50,'coeff'); %计算自相关函数,
% 第一个参数表示计算自相关值的序列
% 第二个参数表示自相关值的最大偏移
% 'coeff'使序列规范化
Sf(ii,:)=fftshift(abs(fft(Rx(ii,:)))); %求傅里叶变换,并将得到的图形关于y轴对称
end
Rx_av=sum(Rx)/N2; %自相关估值
Sf_av=sum(Sf)/N2; %功率谱密度的平均值
subplot(2,1,1);plot(lags,Rx_av);title('自相关函数')
subplot(2,1,2);plot(lags,Sf_av);title('功率谱密度')
axis([-50 50 0 2]) 2.带通随机过程
例.已知一噪声的自相关函数为,R(x)=sinc(2Bx)cos(2πf0x),其中B=20,f0=100,求该随机过程的功率谱密度。
程序如下:
clear all
ts=0.002; %设定抽样间隔
tao=-1:ts:1;
B=20;
f0=100;
R=sinc(2*B*tao).*cos(2*pi*f0*tao); %计算自相关函数的值
fs=1/ts;%抽样频率
df=fs/length(tao); %计算频率分辨率
f=-fs/2:df:fs/2-df; %生成频率矢量
S=fft(R)/fs; %计算功率谱密度
subplot(2,1,1);plot(tao,R);title('自相关函数');xlabel('tao');ylabel('R')
subplot(2,1,2);plot(f,fftshift(abs(S)));title('功率谱密度');xlabel('f');ylabel('S')3.随机过程通过线性系统
例.考虑一个白噪声序列Xn通过一个滤波器产生的序列,滤波器的脉冲响应为
f(n) =
{0.6n,0,n>=0n<0
输入序列均值为0,方差为1的高斯分布随机变量的一个独立同分布,求输出过程的自相关函数和功率谱密度。
程序如下:
clear all
N1=2000;
N2=100;
x=randn(N2,N1);
for ii=1:N2 %计算输入序列经过滤波器后的输出序列
y(ii,1)=x(ii,1);
for jj=2:N1
y(ii,jj)=0.6*y(ii,jj-1)+x(ii,jj);
end
[Ry(ii,:),lags]=xcorr(y(ii,:),50,'coeff');
Sf(ii,:)=fftshift(abs(fft(Ry(ii,:))));
end
Ry_av=sum(Ry)/N2;
Sf_av=sum(Sf)/N2;
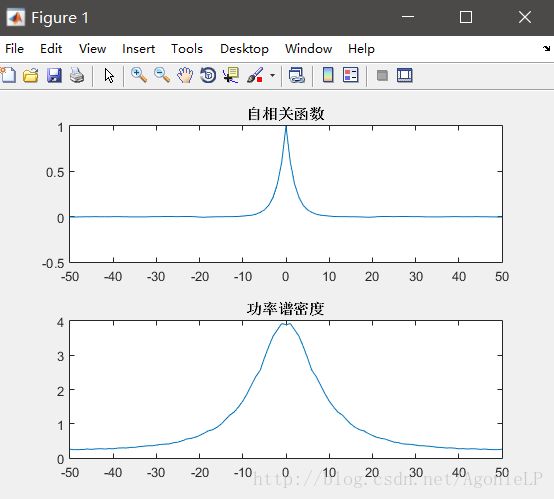
subplot(2,1,1);plot(lags,Ry_av);title('自相关函数')
subplot(2,1,2);plot(lags,Sf_av);title('功率谱密度')