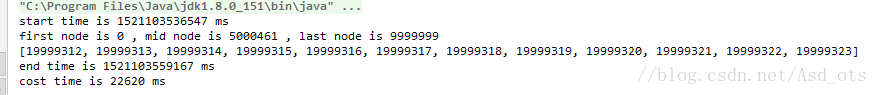插入排序，归并排序，快速排序的实现和速度比较（包含二分法查找所有匹配元素）

最近在学习排序算法，实现后比较了花费时间情况，现在总结一下

插入排序的时间复杂度是O(n²)，是一种很直观的排序方式。归并排序为O（nlogn），实现起来也比较简单。快速排序平均时间复杂度也是O(nlogn），实现起来比归并复杂一些。经过比较发现快速排序比归并排序要快一些，大概一倍的时间，数据越大，效果越明显。我尝试用5000万长度的随机数组成的数组进行排序，归并排序大概用了50s左右，期间出现过oom，比较消耗堆栈的空间，而快速排序则很稳定，实现的时候的不会额外创建数组，全是在原数组之上的操作，主要是swap操作，多次测试大概只用了20s左右的时间，也是5000万长度的数据。然后做了简单的二分查找，实现了对排序数组的指定的相等元素全部查找出来。

这是归并排序花费的时间：

这是快速排序花费的时间

下面是具体代码实现：

import java.util.ArrayList;
import java.util.List;
import java.util.Random;

public class MergeSort {

    private static > void mergeSort(T [] arr){

       // T [] tempArr= (T []) new Comparable[arr.length];

        mergeSort(arr, 0, arr.length - 1);

    }

    private static > void mergeSort(T[] arr, int left, int right) {

        if (left < right){
            int mid = (left + right) / 2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }




    }

    private static > void merge(T[] arr, int left, int mid, int rightEnd) {

        T [] temp = (T []) new Comparable[rightEnd - left + 1];
      //  System.out.println(temp);

        int leftEnd = mid;
        int right = mid + 1;
        int tempPos = 0;
        int numOfObj = rightEnd - left + 1;

        while(left <= leftEnd && right <= rightEnd){
            if (arr[left].compareTo(arr[right]) <= 0){
                temp[tempPos ++] = arr[left ++];
            }else {
                temp[tempPos ++] = arr[right ++];
            }
        }

        while (left <= leftEnd) {
            temp[tempPos++] = arr[left++];
        }

        while (right <= rightEnd) {
            temp[tempPos++] = arr[right++];
        }
       for (int i = numOfObj - 1; i >= 0;){
            arr[rightEnd--] = temp[i--];
        }
    }


    private static > void quickSort(T [] arr){
        quickSort(arr, 0, arr.length - 1);
    }

    private static > void quickSort(T[] arr, int start, int end) {
        if (end - start < 8) {
            insertSort(arr, start, end);
        } else {

            T key = prepQuickSort(arr, start, end);
            int leftIndex = start;
            int rightIndex = end - 1;
            for ( ; ;) {
                while (arr[++leftIndex].compareTo(key) < 0) { }
                while (arr[--rightIndex].compareTo(key) > 0) { }

                if (leftIndex > rightIndex) {
                    break;
                } else {
                    swapByReference(arr, leftIndex, rightIndex);
                }
            }
            swapByReference(arr, leftIndex, end - 1);

            quickSort(arr, start, leftIndex - 1);
            quickSort(arr, leftIndex + 1, end);
        }
    }

    private static > T prepQuickSort(T[] arr, int left, int right) {

        int mid = (left + right) / 2;
        if (arr[left].compareTo(arr[mid]) > 0)
            swapByReference(arr, left, mid);
        if (arr[left].compareTo(arr[right]) > 0)
            swapByReference(arr, left, right);
        if (arr[mid].compareTo(arr[right]) > 0)
            swapByReference(arr, mid, right);

        swapByReference(arr, mid, right - 1);
        return arr[right -1];
    }

    private static  > void insertSort(T[] arr) {
        insertSort(arr, 0, arr.length);
    }

    private static > void insertSort(T[] arr, int start, int end) {
        T min;
        int index;
        for (int i = start; i < end -1; i ++){
            min = arr[i];
            index = i;
            for (int j = i + 1; j < end; j++){
                if (min.compareTo(arr[j]) > 0){
                    min = arr[j];
                    index = j;
                }
            }
            swapByReference(arr, i, index);
        }

    }

    private static > void swapByReference(T[] arr, int before, int after) {
        if (before == after)
            return;
        else {
            T tmp;
            tmp = arr[before];
            arr[before] = arr[after];
            arr[after] = tmp;
        }

    }

    public static > List binarySearch(T [] arr, T goal){

        if (arr == null || arr.length < 1 )
            return null;

        int left = 0;
        int right = arr.length -1;
        if (arr[left].compareTo(goal) > 0 || arr[right].compareTo(goal) < 0)
            return null;
        int mid = right / 2;

        while(left < right){
            if (arr[mid].compareTo(goal) == 0){
                List list = new ArrayList();

                int eqLeft = getEqualsBound(arr, mid, false);
                int eqRight = getEqualsBound(arr, mid, true);

                for (int index = eqLeft; index <= eqRight; index ++){
                    list.add(index);
                }
                return list;

            } else if (arr[mid].compareTo(goal) > 0)
                right = mid - 1;
            else
                left = mid + 1;
            mid = (left + right) / 2;
        }
        return  null;
    }

    private static > int getEqualsBound(T[] arr, int location, boolean sequence) {
        int result = location;
        if (sequence){
            while(arr[location].compareTo(arr[++result]) == 0){ }
            return result - 1;
        }else {
            while(arr[location].compareTo(arr[--result]) == 0){ }
            return result + 1;
        }
    }


    public static void main(String[] args) {

        Integer[] arr = {16,2,4,3,1,5,6,0,2,4,3,11,14,16,12,9,8,11,13,15,18,20,19,11,22,23,9,6,3,4,5,1,1,0,7,4,3,4,5,1,14,16};
        Integer[] arr1 = {2,2,2,2,2,2,2,2,2,2};

        List list = new ArrayList();
        Random random = new Random();
        for (int i= 0; i< 50000000; i++){
            list.add(random.nextInt(10000000));
        }
        Integer [] mkArr = list.toArray(new Integer[0]);

        long startTime = System.currentTimeMillis();
        System.out.println("start time is " + startTime + " ms");

        quickSort(mkArr);
        System.out.println("first node is " + mkArr[0] + " , mid node is " + mkArr[mkArr.length/2] + " , last node is " + mkArr[mkArr.length -1]);
        System.out.println(binarySearch(mkArr, 4000000));
        long stopTime = System.currentTimeMillis();
        System.out.println("end time is " + stopTime + " ms");
        System.out.println("cost time is " + (stopTime - startTime) + " ms");

    }