参考
白话经典贝塞尔曲线及其在 Android 中的应用
Path从懵逼到精通(2)——贝塞尔曲线
干货!设计师必须掌握的贝塞尔曲线的秘密
使用 Adobe Illustrator 绘制复杂光滑曲线的一种策略
一、前言
谈到贝塞尔曲线可能不少人会浮现它高大上的数学公式。然而,在实际应用中,并不需要我们去完全理解或者推导出公式才能应用得上。实际情况是,即使真的只是一个学渣,我们应该也能很轻松的掌握贝塞尔曲线的大致原理及其在开发中的实际应用。
二、二阶贝塞尔曲线的原理
贝塞尔曲线有一阶、二阶、三阶....一直到 N 阶。实际应用中我们常用的是二阶、三阶,高阶可以由低阶来实现。咱们这里以二阶为例来讲解一下贝塞尔曲线的基本原理。
二阶贝塞尔曲线三要素
1 个起点,1 个终点,1 个控制点
这个是我们要知道的第一个知识点,而三阶的话就是 2 个控制点,四阶的话就是 3 个,以此类推,N 阶的话就是 N - 1 个控制点。而起点和终点始终只有一个。
下面我们来手动画一个贝塞尔曲线。
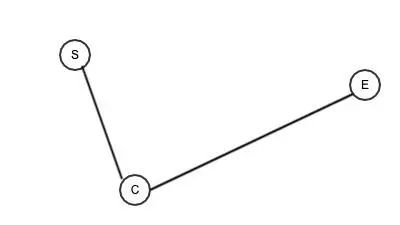
1.绘制 1 个起点,1 个终点和 1 个控制点,分别为 S 、E、C。然后将 SC、CE 分别连线。如下图所示。
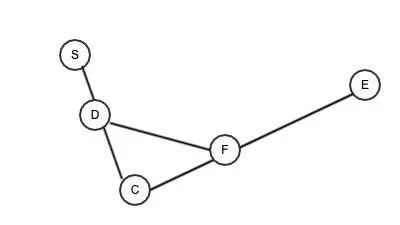
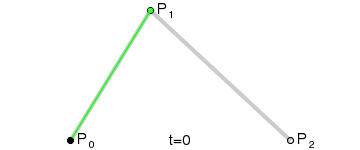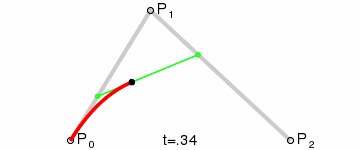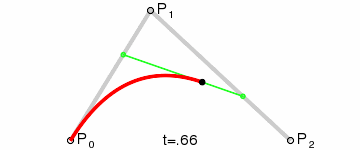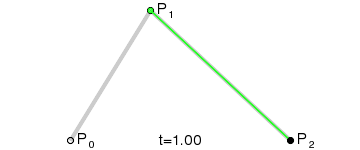
2.从点 S 向 C 出发找到一个 D 点,从 C 向 E 出发找到一个 F 点,使得SD / SC = CF / CE。然后连接 DF。如下图所示。
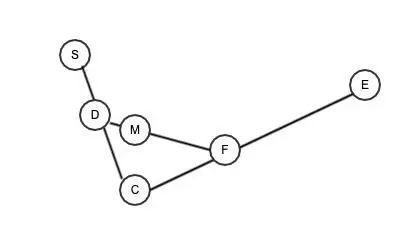
3.在 DF 之间找到点 M,使得SD / SC = CF / CE = DM / DF
总结下:
- (1) 二阶贝塞尔中,起初是 3 个点,然后我们再找 2 个点,然后再找 1 个点。这个点就是我们要找到的点。
- (2) 我们需要由 S 向 C 出发,由 C 向 E 出现,找到所有的 D 和 F,再找到所有的 M。
- (3) 将所有的 M 连接起来就构造出了最后的所需要的贝塞尔曲线了。
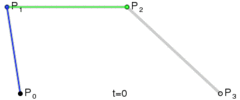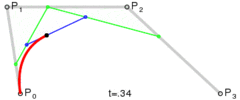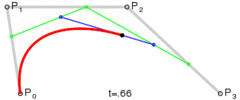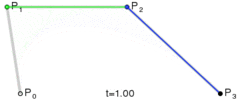
借用一个图,来详细观察一下其构造的过程。
三、三阶贝塞尔曲线
三阶和二阶是类似的:
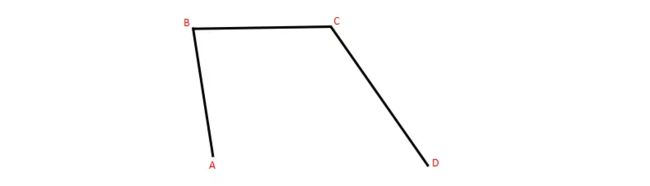
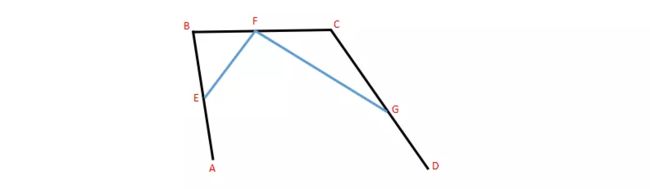
1.连接 A,B 形成 AB 线段,连接 B,C 形成 BC 线段,连接 C,D 形成 CD 线段。
2.在AB线段取一个点 E,BC 线段取一个点 F,CD 线段取一个点 G,使其满足条件: AE/AB = BF/BE = CG/CD。连接 E,F 形成线段 EF,连接 F,G 形成线段 FG。
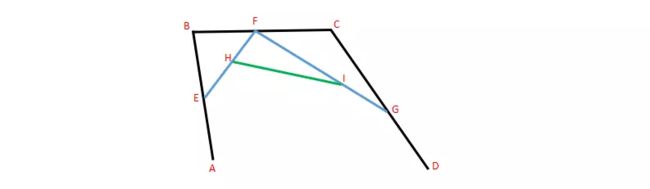
3.在EF线段取一个点 H,FG 线段取一个点 I,使其满足条件: AE/AB = BF/BE = CG/CD = EH/EF = FI/FG。连接 H,I 形成线段 HI。
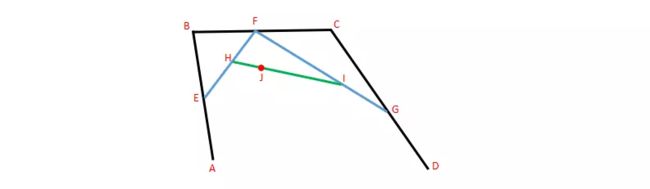
4.在 HI 线段取一个点 J,使其满足条件: AE/AB = BF/BE = CG/CD = EH/EF = FI/FG = HJ/HI。
5.而满足这些条件的所有的J点所形成的轨迹就是三阶贝塞尔曲线,动态过程如下:
关于贝塞尔曲线的原理,介绍这么多就够了,再说就是多余。如果实在还不明白或者想深入的,推荐以下链接。当然,更建议自己多琢磨琢磨。
贝塞尔曲线 总结
贝塞尔曲线扫盲
贝塞尔曲线游戏
bezier-circle
四、cocos的bezier
1.从CCActionInterval.js中的API源码中可以看出,bezierTo实现的是二阶贝塞尔。
var bezier = [cc.v2(0, windowSize.height / 2), cc.v2(300, -windowSize.height / 2), cc.v2(300, 100)];
var bezierForward = new cc.BezierBy(3, bezier);
s.runAction(bezierForward);
部分源码如下:
update:function (dt) {
dt = this._computeEaseTime(dt);
if (this.target) {
var locConfig = this._config;
var xa = 0;
var xb = locConfig[0].x;
var xc = locConfig[1].x;
var xd = locConfig[2].x;
var ya = 0;
var yb = locConfig[0].y;
var yc = locConfig[1].y;
var yd = locConfig[2].y;
var x = bezierAt(xa, xb, xc, xd, dt);
var y = bezierAt(ya, yb, yc, yd, dt);
...