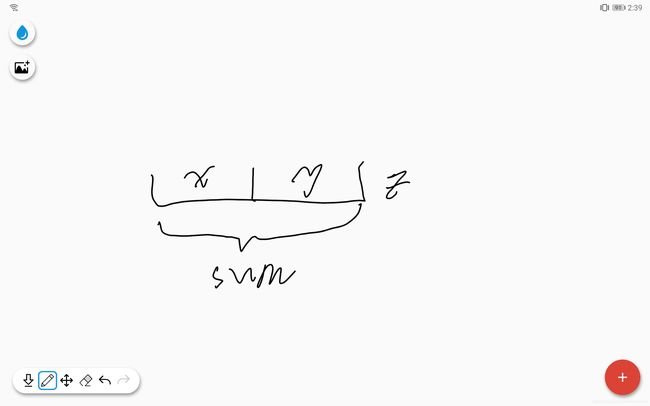2019杭电多校第二场 G - Find the answer （权值线段树）

题目链接：HDU - 6609

题意：多组输入，给定一个n，m，再给一个长度为n的序列，对于所有的你可以选择一些下标范围在范围内的数字变为0，使得前缀和小于等于m，问对于每个i需要改变的最小次数。i与i-1是独立的两个问题。注意嗷，这个题行末有空格

权值线段树，对于每个数字我们肯定是贪心的减掉较大的数字肯定会使得答案更小，那么问题转化成了对于第i个位置，假设前面的数字已经有序了，从i-1开始向前减掉一些数字即可。

先离散化。

而权值线段树便可以使得序列有序，维护数字出现次数和，离散化后第k个下标代表的具体数字的区间和。

从前往后枚举i，如上图，假设要减掉的数字和为y，剩下的为x，当前枚举到的数字为z，x+y=sum。

要使得,是不是要找一个y使得，且长度最小。

那么就可以到线段树中查了，根据贪心的思想，肯定优先考虑右子树，如果右子树的值大于等于y，那么直接去找，否则右子树全取，y减去右子树的和，再去左子树找，即可。

#include
using namespace std;

const int maxn=2e5+7;

typedef long long ll;
int b[maxn];
int a[maxn];
int m;
void quchong(int n){
    sort(b+1,b+1+n);
    m=unique(b+1,b+1+n)-b-1;
}

int getid(int x){
    return lower_bound(b+1,b+1+m,x)-b;
}

int ci[maxn<<2|1];

ll sum[maxn<<2|1];

void pushup(int l,int r,int k){
    ci[k]=ci[k<<1]+ci[k<<1|1];
    sum[k]=sum[k<<1]+sum[k<<1|1];
}

void build(int l,int r,int k){
    ci[k]=sum[k]=0;
    if(l==r) return ;
    int mid=(l+r)>>1;
    build(l,mid,k<<1);
    build(mid+1,r,k<<1|1);
}

void updata(int l,int r,int k,int id,int val){
    if(l==r){
        ++ci[k];
        sum[k]+=b[l];
        return ;
    }
    int mid=(l+r)>>1;
    if(id<=mid) updata(l,mid,k<<1,id,val);
    else updata(mid+1,r,k<<1|1,id,val);
    pushup(l,r,k);
}

int myfind(int l,int r,int k,ll x){
    if(l==r){
        if(sum[k]>=x) return ceil(x*1.0/b[l]);
        return ci[k];
    }
    int mid=(l+r)>>1;
    if(sum[k<<1|1]>=x){
        return myfind(mid+1,r,k<<1|1,x);
    }
    if(sum[k<<1|1]+sum[k<<1]>=x)
        return ci[k<<1|1]+myfind(l,mid,k<<1,x-sum[k<<1|1]);

    return 0;
}

int main(){
    int t;
    int n,q;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&q);
        for(int i=1;i<=n;++i){
            scanf("%d",&a[i]);
            b[i]=a[i];
        }
        ll s=0;
        quchong(n);
        build(1,m,1);
        printf("0 ");
        updata(1,m,1,getid(a[1]),1);
        s+=a[1];
        for(int i=2;i<=n;++i){
            s+=a[i];
            if(s<=q) printf("0 ");
            else
                printf("%d ",myfind(1,m,1,a[i]-q+sum[1]));
            updata(1,m,1,getid(a[i]),1);
        }
        printf("\n");
    }

    return 0;
}