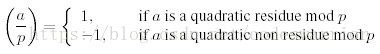Jacobi symbol（二次剩余+欧拉准则）

Jacobi symbol

Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that x 2 ≡ a (mod p), and a quadratic non residue otherwise. Lagrange introduced the following notation, called the Legendre symbol, L (a,p):

For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:

The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) J (a, p2)… J (a, pm), p1…pm is the prime factor of n. Input
Two integer a and n, 2 < a< =10 6，2 < n < =10 6，n is an odd number.
Output
Output J (a,n)
Sample Input

3 5
3 9
3 13

Sample Output

-1
0
1

题意：

求J（a，n）

分析：二次剩余，欧拉准则！

在数论中，特别在同余理论裏，一个整数 X X 对另一个整数 p p 的二次剩余（英语：Quadratic residue）指 X X 的平方 X2 X 2 除以 p p 得到的余数。

当对于某个 d及某个X，式子X2≡d(modp)成立时，称“d是模p d 及 某 个 X ， 式 子 X 2 ≡ d ( mod p ) 成 立 时 ， 称 “ d 是 模 p 的二次剩余”

当对于某个 d及某个X，X2≡d(modp)不成立时，称“d是模p d 及 某 个 X ， X 2 ≡ d ( mod p ) 不 成 立 时 ， 称 “ d 是 模 p 的二次非剩余”

欧拉准则：

若p是奇质数且p不能整除d，则：
d是模p的二次剩余当且仅当：

dp−12≡1(modp) d p − 1 2 ≡ 1 ( mod p )

d是模p的非二次剩余当且仅当：

dp−12≡−1(modp) d p − 1 2 ≡ − 1 ( mod p )

以勒让德符号表示，即为：

dp−12≡(dp)(modp) d p − 1 2 ≡ ( d p ) ( mod p )

算是个求一个数是否是二次剩余的模板吧

code:

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
bool isprime[maxn];
int prime[maxn],tot;
void init(){
    tot = 0;
    memset(isprime,true,sizeof(isprime));
    isprime[0] = isprime[1] = false;
    for(int i = 2; i < maxn; i++){
        if(isprime[i]){
            prime[tot++] = i;
            for(int j = i + i; j < maxn; j += i){
                isprime[j] = false;
            }
        }
    }
}

int q_pow(int a,int n,int m){
    ll ans = 1;
    ll x = a;
    while(n){
        if(n & 1)
            ans = ans * x % m;
        x = x * x % m;
        n >>= 1;
    }
    return ans % m;
}

int solve(int a,int p){
    if(a % p == 0) return 0;
    return q_pow(a,(p-1)/2,p) == 1 ? 1 : -1;
}
int main(){
    int a,n;
    init();
    while(~scanf("%d%d",&a,&n)){
        int ans = 1;
        if(!isprime[n]){
            for(int i = 0; i < tot && prime[i] <= n; i++){
                if(n % prime[i]) continue;
                int cnt = 0;
                while(n % prime[i] == 0){
                    cnt++;
                    n /= prime[i];
                }
                int t = solve(a,prime[i]);
                if(t == -1 && cnt % 2 == 0) t = 1;//注意个数如果是-1并且偶数个相乘那就成1了
                ans *= t;
            }
        }
        else{
            ans = solve(a,n);
        }
        printf("%d\n",ans);
    }
    return 0;
}