R入门(三) ----拟合、添加公式
小心情
跟着大鹏的《学R》,昨晚自己竟然梦见自己躺在简单易懂的文字里面,所向披靡。临睡前还想着给大鹏写一份感谢信呢,可能就是因为这个,自己太激动了吧。似睡非睡的夜晚,早起脑壳还晕晕的。一些从简,凡事从简,多么美好。想起了研究生教我们商务英语的老师,和我们分享了一些学习英语的心得,让我们不要一来就读那些特别有名的名著,而且又难啃,多一些外国小学水平的,在自己词汇量以下的读物,才会有更多的输入。考完商务英语,又是一个失眠的夜晚,也是想捎去我的感激来着,最后还是放弃捎了。哈哈哈哈。。。不能拖着哇。。。。。
(另一个不开心的小事==>难免被拒绝嘛,虽然有点小失落,没关系,加油!!!)
正文(拟合)
1.线性拟合
lm(y~x):因变量~自变量,强制通过原点时,令截距为0,即 lm(y~x+0)
wp <- as.data.frame(WorldPhones)
wp$year <- as.numeric(rownames(wp))
m <- lm(wp$Asia~wp$Europe)
m0 <- lm(wp$Asia~wp$Europe+0)
#查看模型结果
msum<- summary(m)
msum
example(lm) #展示的就是lm()帮助页中的'Examples'
| 函数返回 | 值 |
|---|---|
| summary() | 主要统计量 |
| anova() | 方差分析表 |
| coef(),coefficients() | 回归系数 |
| confint() | 回归系数的置信区间 |
| deviance() | 残差平方和 |
| effects() | 正交效应向量(Vector of orthogonal effects) |
| fitted() | 拟合的Y值向量Vector of fitted y values |
| residuals(),resid() | 模型残差Model residuals |
| vcov() | 主参数的协方差矩阵 |
plot(m)
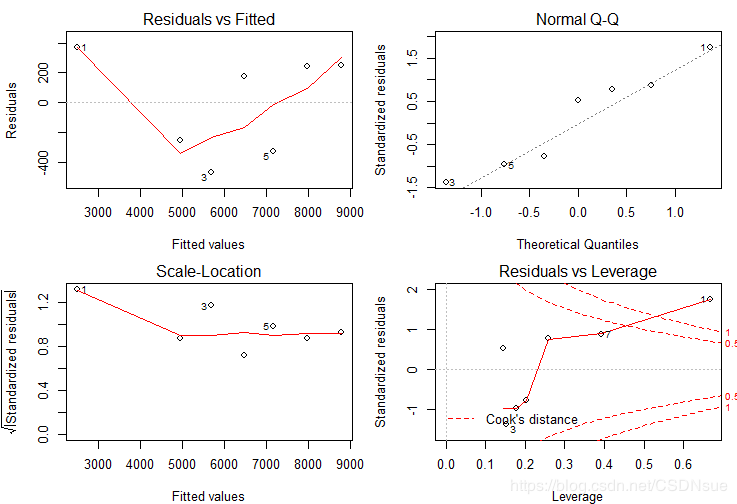
plot()再次展示了强大的威力。这四张图里,第一张是以拟合值为横坐标、残差为纵坐标的对比图,用来展示残差是否均匀分布在直线y=0两侧;第二张是残差Q-Q图,用来展示残差是否符合正态分布:第三张是以拟合值为横坐标、标准残差平方根为纵坐标的对比图,仍然是用来展示残差分布状况的;第四张是以杠杆值为横坐标、标准残差为纵坐标的对比图,展示影响回归结果的异常点。
#在plot(y,x)的散点图中,加入线性拟合的直线,m是进行lm()线性拟合的结果
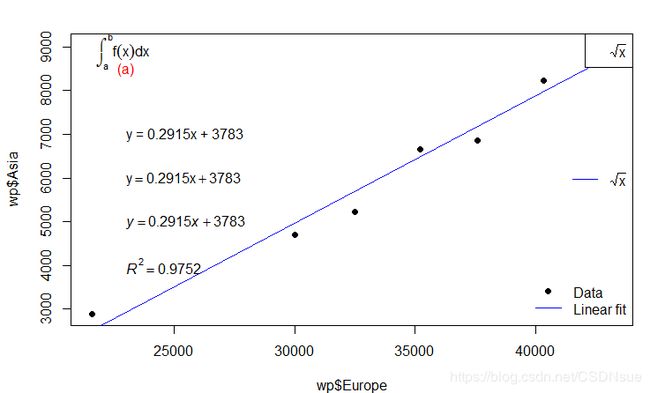
plot(wp$Asia~wp$Europe)
abline(m,col='red')
绘图区添加数学表达式
par(mfrow=c(1,1))
plot(x = wp$Europe,y = wp$Asia,pch=19)
abline(m,col='blue')
legend('bottomright',pch = c(19,NA),lty = c(NA,1),
legend = c('Data','Linear fit'),
col = c('black','blue'),bty = 'n')
注释:
- legend函数中
-
pch参数和lty参数???
pch是打头的p,point针对的是点;同理,lty打头的是l,line针对的是线。 -
col表示的是图形中点和线的颜色,盒的形状为无
text(x=23000,y = 8500,labels = '(a)',col = 'red')
#将方程看作是一个字符串添加到图形中去
eqlm1 <- 'y = 0.2915x + 3783'
text(x = 23000,y = 7000,labels = eqlm1,adj = 0)
#斜体表示的x和y,要借助expression,同时称号不能省略,等号用双等号==表示
eqlm2 <- expression(y == 0.2915 * x +3783)
text(x = 23000,y = 6000,labels = eqlm2,adj = 0)
#同样是用expression()函数,此时x和y用意大利斜体表示
eqlm3 <- expression(italic(y) == 0.2915 * italic(x) + 3783)
text(x = 23000,y = 5000,labels = eqlm3,adj = 0)
eqr2 <- expression(italic(R)^2 == 0.9752)
text(x = 23000,y = 4000,labels = eqr2,adj = 0)
#在expression中遇见^,会自动识别出上角标
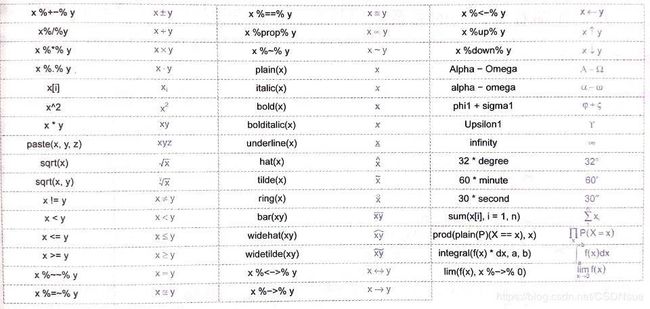
#expression()函数生成的表达式,可以用在text(),legend(),mtext(),xlab(),ylab()中
#插入根号
txt1 <- expression(sqrt(x))
legend('topright',legend = txt1)
legend('right',legend=txt1,lty=1,col='blue',bty='n')
#插入积分符号
txt2 <- expression(integral(f(x) * dx,a,b))
legend('topleft',legend = txt2,col = 'blue',bty = 'n')
demo(plotmath) #可以直接显示出expression()中符号如何表达,优秀!
2.非线性拟合
nls(),(Non-Linear Simulation) 非线性模拟,实现y与x之间的非线性方程
> #非线性拟合
> #根据均匀分布,正态分布生成随机数
> x <- seq(from=0,to = 50,by = 1)
> y <- runif(n=1,min = 5,max = 15)*exp(-runif(n = 1,min = 0.01,max = 0.05)*x)+
+ rnorm(n = 51,mean = 0,sd = 0.5)
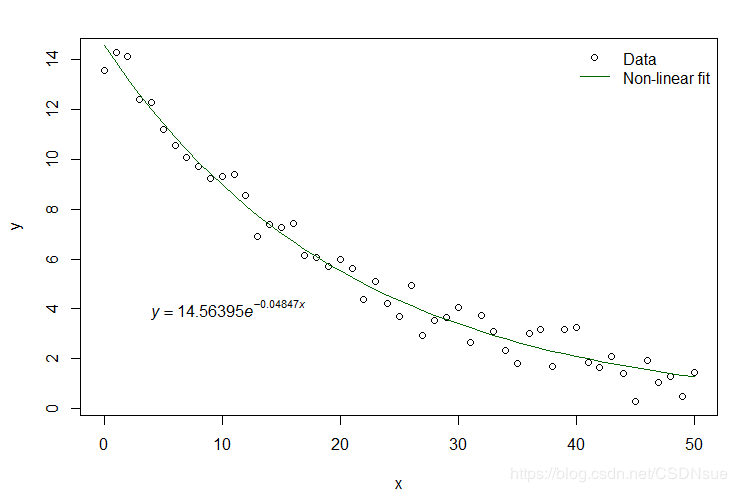
> plot(x,y)

上图 y y y与 x x x之间的关系式为: y = a e b x y=ae^{bx} y=aebx
根据上图中的截距(0,14)(40,2)进行a,b初始值设置,放在列表list()中
> a_start <- 14
> b_start <- -log(2/a_start)/40
> m <- nls(y ~ a*exp(-b*x),
+ start = list(a=a_start,b=b_start))
> m
Nonlinear regression model
model: y ~ a * exp(-b * x)
data: parent.frame()
a b
14.56395 0.04847
residual sum-of-squares: 16.79
Number of iterations to convergence: 3
Achieved convergence tolerance: 2.017e-07
> #设置初始值,最终经过三次迭代得到a,b的值,分别为14.56395和0.04847
> #真实值与拟合值得相关系数,predict(m),就是根据模型及x,预测得到的
> cor(y,predict(m))
[1] 0.988709
> summary(m)
Formula: y ~ a * exp(-b * x)
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 14.563951 0.253946 57.35 <2e-16 ***
b 0.048474 0.001311 36.98 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5854 on 49 degrees of freedom
Number of iterations to convergence: 3
Achieved convergence tolerance: 2.017e-07
作业4.3
#向图中添加模型的拟合曲线,用lines函数
#不能用abline()的原因是,拟合的不是直线,是曲线,可以根据模型预测出的值,作为曲线的y
plot(x,y)
lines(x,y = predict(m),col='darkgreen')
eqnls <- expression(italic(y) == 14.56395 * italic(e)^{-0.04847*italic(x)})
text(x = 4,y = 4,labels = eqnls,adj = 0)
legend('topright',pch = c(1,NA),lty = c(NA,1),
legend = c('Data','Non-linear fit'),
col = c('black','darkgreen'),
bty = "n")