高等数学--方程的近似解（六）

目的： 在科学技术问题中，经常会遇到求解高次代数方程或其他类型方程的问题，要求出这类方程实根的精确值，往往比较困难，需要寻找方法来获取方程的近似解。

步骤：
①先画出复杂方程y=f(x)的大致图形，从图上定位出它与x轴的交点大概位置，这一步工作称为根的隔离，获取的区间[a,b]称为隔离区间。
②以根的隔离区间作为初始近似值，逐步改善其精确度，直至满足要求。

二分法，对分法

设f(x)在区间[a,b]上连续，f(a)*f(b)<0,且方程f(x)=0在(a,b)内仅有一个实根ε，于是[a,b]既是这个根的一个隔离区间。
取[a,b]的中点ε1=（a+b）/2，计算f(ε1)。
如果恰好f(ε1)=0，方程的根自然就是ε=ε1。
如果f(ε1)与f(a)同号，那么新a1=ε1，新b1=b，如果f(ε1)与f(b)同号，那么新a1=a，新b1=ε1，在新隔离区间再找。
重复以上步骤。

例1 求方程x^3 + 1.1x ^2+0.9x-1.4=0 实根的近似解
解： 令y=x^3+1.1x ^2+0.9x-1.4，画出图形：

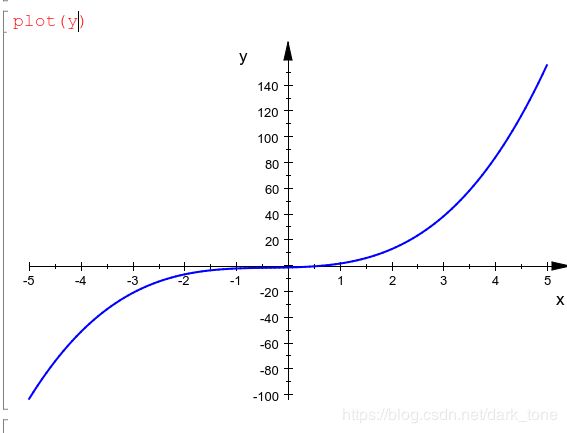
肉眼大概看出隔离区间是[-1,1]。
①先令ε1=(a+b)/2=0，求出f(0)=-1.4 ,f(-1)=-2.2 ，同号，那么新a1=ε1=0，b1=b=1，隔离区间为[0,1]
②再令ε2=(a1+b1)/2=0.5，求出f(0.5)=-0.55，与f（a1）同号，那么新a2=ε2，b2=b=1,隔离区间为[0.5,1]
………………
………………
求出当ε10=0.670，f(ε10)=-0.002，满足近似条件。

切线法，牛顿迭代法

设f(x)在区间[a,b]上具有二阶导数，f(a)f(b)<0，且f’(x)及f’’(x)在[a,b]上保持定号，在上述条件下方程f(x)=0在(a,b)内有唯一实根。
考虑用曲线弧一端的切线来代替曲线弧，从而求出近似值。
根据导数的切线公式：
y-y0=f’(x0)(x-x0)，从而得出点xn，yn与x轴相交的近似值是:
x(n+1)=xn- yn/f’(xn)

例2 用切线法求方程x^3 + 1.1x ^2+0.9x-1.4=0 实根的近似解。
解：令y=x^3+1.1x ^2+0.9x-1.4，在隔离区间[0，1]内
y’=3x ^2+2.2x+0.9 >0, y’’=6*x+2.2 >0
因为f(1)与y’‘同号，取x0=1
x1= 1- f(1)/f’(1)≈0.738
x2=0.738 - f(0.738)/f’(0.738)≈0.674
……
x4=0.671 - f(0.671)/f’(0.671)≈0.671
至此，计算无法继续了，于是 0.670< ε <0.671

割线法

利用切线法有先觉条件的，比如f’(x)也难以求解。
可以利用割线法来求解：
x（n+1）= xn- （xn-x（n-1））/f（xn）-f（x（n-1）） * f(xn)

例3 用割线法求方程x^3 + 1.1x ^2+0.9x-1.4=0 的近似解。
解:取x0=1，x1=0.8
x2 = x1- (x1-x0)/(f(x1)-f(x0)) * f(x1) ≈ 0.699
x3 =x2- (x2-x1)/(f(x2)-f(x1)) * f(x2) ≈0.672
x4 = x3- (x3-x2)/(f(x3)-f(x2)) * f(x3) ≈ 0.671

故可以用0.671作为根的近似值。

总结： 二分法最容易理解，计算起来也不麻烦，但是步骤太多。 割线法相对步骤少，计算起来不麻烦，但算起来容易出错，要带入好几个不同变量。
用matlab求解方程到无需这么麻烦，直接solve就能获得结果。

介值定理： f(a)*f(b)<0, 那么 方程f(x)在(a,b)内有一个实根ε，满足f(ε)=0.