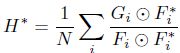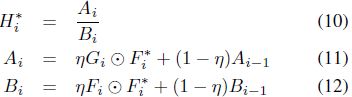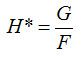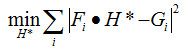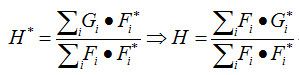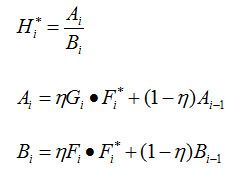目标追踪——相关滤波追踪论文翻译：Visual Object Tracking using Adaptive Correlation Filters

Abstract

    Although not commonly used, correlation filters can track complex objects through rotations, occlusions and other distractions at over 20 times the rate of current state-ofthe-art techniques. The oldest and simplest correlation filters use simple templates and generally fail when applied to tracking. More modern approaches such as ASEF and UMACE perform better, but their training needs are poorly suited to tracking. Visual tracking requires robust filters to be trained from a single frame and dynamically adapted as the appearance of the target object changes.

    This paper presents a new type of correlation filter, a Minimum Output Sum of Squared Error (MOSSE) filter, which produces stable correlation filters when initialized using a single frame. A tracker based upon MOSSE filters is robust to variations in lighting, scale, pose, and non-rigid deformations while operating at 669 frames per second. Occlusion is detected based upon the peak-tosidelobe ratio, which enables the tracker to pause and resume where it left off when the object reappears.

    Note: This paper contains additional figures and content that was excluded from CVPR 2010 to meet length requirements.

1、摘要

      尽管相关滤波器不常用，但它可以追踪复杂的物体，并且比当前技术水平快20倍以上，尽管可能会有旋转、遮挡或者其它的干扰。最古老和最简单的相关滤波器使用简单的模板，，但是应用于实际跟踪上，一般会失败。比较现代的方法，比如 ASEF 和UMACE ，表现更良好一些。但是他们的训练需求很难应用于跟踪。视觉追踪需要从一帧图像中训练一个鲁棒的滤波器，并且这个滤波器能随着目标物体的改变（比如尺度等），动态地变化调整。

      本文提出一种新的相关滤波器——最小化平方和误差（MOSSE）滤波器，当使用一帧图像进行初始化的时候，可以产生很多稳定的相关滤波器。当存在光照、尺度、姿态和非刚性变形等，基于MOSSE 滤波器的追踪器是鲁棒的，并且，可以秒运行 669 帧。通过峰值-旁瓣比，能够检测出遮挡，此时，追踪器停止追踪。当目标物体再次出现时，追踪器从它上次停止的地方，重新开始追踪。

1 Introduction

    Visual tracking has many practical applications in video processing. When a target is located in one frame of a video, it is often useful to track that object in subsequent frames. Every frame in which the target is successfully tracked provides more information about the identity and the activity of the target. Because tracking is easier than detection, tracking algorithms can use fewer computational resources than running an object detector on every frame.

      视觉追踪在视频处理中有很多实际的用处。当一个目标物体在视频中的某一帧中被确定时，在接下来的视频帧序列中，追踪此目标往往是比较有意义的。在目标被成功追踪的每一帧中，提供了关于目标的身份和活动的的更多信息。跟踪比检测稍微容易些，因为追踪算法不必运算了目标检测器，因此，追踪所耗费的计算资源更少。

    Visual tracking has received much attention in recent years. A number of robust tracking strategies have been proposed that tolerate changes in target appearance and track targets through complex motions. Recent examples include: Incremental Visual Tracking (IVT) [17], Robust Fragments-based Tracking (FragTrack) [1], Graph Based Discriminative Learning (GBDL) [19], and Multiple Instance Learning (MILTrack) [2]. Although effective, these techniques are not simple; they often include complex appearance models and/or optimization algorithms, and as result struggle to keep up with the 25 to 30 framesper second produced by many modern cameras (See Table1).

    近些年来，视觉追踪备受关注。一系列较鲁棒的追踪策略被提出，来适应目标外观的变化。最近的算法有增量视觉追踪 IVT，鲁棒的基于目标分块的跟踪 Frag Track，甄别学习 GBDL 以及多实例学习。这些技术是有效的，但是技术实现上并不简单。他们通常包括复杂的外观模型和优化算法，并且，实时性也保证不了，适应不了 25帧或者30帧的摄像头。见下表：

      

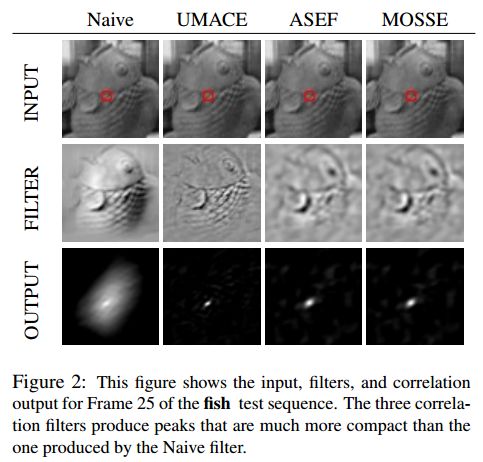
     In this paper we investigate a simpler tracking strategy. The targets appearance is modeled by adaptive correlation filters, and tracking is performed via convolution. Naive methods for creating filters, such as cropping a template from an image, produce strong peaks for the target but also falsely respond to background. As a result they are not particularly robust to variations in target appearance and fail on challenging tracking problems. Average of Synthetic Exact Filters (ASEF), Unconstrained Minimum Average Correlation Energy (UMACE), and Minimum Output Sum of Squared Error (MOSSE) (introduced in this paper) produce filters that are more robust to appearance changes and are better at discriminating between targets and background. As shown in Figure 2, the result is a much stronger peak which translates into less drift and fewer dropped tracks. Traditionally, ASEF and UMACE filters have been trained offline and are used for object detection or target identification. In this research, we have modified these techniques to be trained online and in an adaptive manor for visual tracking. The result is tracking with state of the art performance that retains much of the speed and simplicity of the underlying correlation based approach .

      本文提出一种更简单的追踪策略。通过自适应相关滤波器对目标外形进行建模，并通过卷积进行跟踪。创建滤波器有几种简单的方法，比如，从一帧图像中裁剪模板，为目标生成强大的峰值，但是也会对背景产生响应。因此，对于目标外观的变化，跟踪结果不是特别鲁棒，在一些具有挑战性的追踪场景上会失败。ASEF ,UMACE以及 本文提出的 MOSSE产生的滤波器，对目标外观的改变更加鲁棒，同时，区分目标和背景的效果也更好。如下图所示，结果是一个更强烈的峰值，它会减少目标的漂移和更少的下降轨迹。传统上，ASEF ,UMACE可以进行离线训练，用于目标检测与目标识别。在本文研究中，我们修改了这些技术，使可以在线训练，获得了良好的跟踪表现。同时，我们保留了原来基本方法的速度，并且简化了其过程。

      

    Despite the simplicity of the approach, tracking based on modified ASEF, UMACE, or MOSSE filters performs well under changes in rotation, scale, lighting, and partial occlusion (See Figure 1). The Peak-to-Sidelobe Ratio (PSR), which measures the strength of a correlation peak, can be used to detect occlusions or tracking failure, to stop the online update, and to reacquire the track if the object reappears with a similar appearance. More generally, these advanced correlation filters achieve performance consistent with the more complex trackers mentioned earlier; however, the filter based approach is over 20 times faster and can process 669 frames per second(See Table 1).

      尽管 ASEF,UMACE,或者 MOSSE都比较简单，但是，它们对于旋转变化、尺度、光照和部分遮挡等，表现良好。衡量相关峰强度的峰值旁瓣比（PSR），可用来检测是否有遮挡或者跟踪失败，一旦有，则停止在线学习，并且如果有类似目标物体的出现，则重新开始追踪。更一般地，这些 advanced 滤波器获得了和之前提到的那些复杂的滤波器一样的效果，比那些方法快 20倍，并且每秒处理 669 帧。

    The rest of this paper is organized as follows. Section 2 reviews related correlation filter techniques. Section 3 introduces the MOSSE filter and how it can be used to create a robust filter based tracker. Section 4 presents experimental results on seven video sequences from [17]. Finally, Section 5 will revisit the major findings of this paper.

    本文其余部分组织如下：第二节回顾相关滤波技术。第三节介绍 MOSSE 滤波器，以及如何使用它来创建一个鲁棒的基于滤波器的追踪器。第四部分呈现实验结果。最后，第五部分重新讨论本文主要贡献。

2、Background

    In the 1980’s and 1990’s, many variants of correlation filters, including Synthetic Discriminant Functions (SDF) [7, 6], Minimum Variance Synthetic Discriminant Functions (MVSDF) [9], Minimum Average Correlation Energy (MACE) [11], Optimal Tradeoff Filters (OTF) [16], and Minimum Squared Error Synthetic Discriminant Functions (MSESDF) [10]. These filters are trained on examples of target objects with varying appearance and with enforced hard constraints such that the filters would always produce peaks of the same height. Most relevant is MACE which produces sharp peaks and high PSRs.

      在20世纪八九十年代，相关滤波器有很多变体。比如综合判别函数 SDF，最小化方差综合判别函数 MVSDF，最小化平均相关能（MACE），最优全局滤波器（OTF），最小化平方差综合判别函数（MSESDF），这些滤波器的训练依赖目标物体的外观变化和一些硬约束，因此，总是产生相同高度的峰值。其中最好的是产生尖锐峰值和高的 PSRS的 MACE 滤波器。

    In [12], it was found that the hard constraints of SDF based filters like MACE caused issues with distortion tolerance.The solution was to eliminate the hard constraints and instead to require the filter to produce a high average correlation response. This new type of “Unconstrained” correlation filter called Maximum Average Correlation Height (MACH) led to a variant of MACE called UMACE.

    在文献12中发现，基于像MACE那类方法的包含硬约束的 SDF 滤波器，会造成失真容差问题。解决方法就是消除硬约束，而不是使滤波器产生较高的平均相关响应。这种新型的无约束的相关滤波器被称为最大化 MACH，这也使得 MACE 的进化版称为 UMACE。

    A newer type of correlation filter called ASEF [3] introduced a method of tuning filters for particular tasks. Where earlier methods just specify a single peak value, ASEF specifies the entire correlation output for each training image. ASEF has performed well at both eye localization [3] and pedestrian detection [4]. Unfortunately in both studies ASEF required a large number of training images, which made it too slow for visual tracking.This paper reduces this data requirement by introducing a regularized variant of ASEF that is suitable for visual tracking.

    在文献3一种称为 ASEF新的相关滤波器介绍了一种方法，针对特定的任务调整滤波器。之前的方法仅仅指定了一个峰值，而ASEF对每一帧训练图像都明确指定整个的相关输出。 ASEF 在眼部追踪和行人检测上表现良好。遗憾的是，在这两项研究中，ASEF 需要大量的训练样本图像，这使得跟踪速度非常慢。本文引入了一种 ASEF的正则化变体，更适合于视觉追踪，并且不需要那么多的训练样本。

3 Correlation Filter Based Tracking

    Filter based trackers model the appearance of objects using filters trained on example images. The target is initially selected based on a small tracking window centered on the object in the first frame. From this point on,　tracking and filter training work together. The target is tracked by correlating the filter over a search window in next frame; the location corresponding to the maximum value in the correlation output indicates the new position of the target. An online update is then performed based on that new location.

    （第一句不会翻译）基于追踪的滤波器以物体的外观作为模型。在第一帧中选择一个追踪窗口，来初始化目标。从此时开始，追踪模块和滤波器训练模块同时开始工作。通过将滤波器与下一帧的搜索窗口关联起来，进行目标追踪。与相关输出中的最大值相对应的位置，就是下一帧目标的位置。然后，根据新位置在线更新。(这个部分我解释一下：根据当前图像 patch 目标提取的特征 f 和高斯函数 G ，得到一个相关滤波器 H，然后选取下一帧的特征作为输入，与 H 进行运算，得到响应值最大的候选目标。这就引入了一个问题：滤波器 H 如何被初始化的)

    To create a fast tracker, correlation is computed in the Fourier domain Fast Fourier Transform (FFT) [15]. First, the 2D Fourier transform of the input image: F = F(f), and of the filter: H = F(h) are computed. The Convolution Theorem states that correlation becomes an elementwise multiplication in the Fourier domain. Using the ⒘ symbol to explicitly denote element-wise multiplication and . to indicate the complex conjugate, correlation takes the form:

      

The correlation output is transformed back into the spatial domain using the inverse FFT. The bottleneck in this process is computing the forward and inverse FFTs so that the entire process has an upper bound time of O(P log P) where P is the number of pixels in the tracking window.

    为了创建更快速的追踪器，相关性的计算是通过快速傅里叶变换（FFT），首先，先对输入的图像计算 2D 的傅里叶变换 F = F(f) 和滤波器H = F(h) 。卷积定理指出，在傅里叶域，相关性可以表示成对应元素相乘。我们使用表示对应元素相乘。* 表示共轭复数。相关性的任务可以被描述成：

         （1）

利用逆傅里叶变换 FFT，将相关输出转回到时域。这整个过程的难点是计算傅里叶变换和逆傅里叶变换，使时间复杂度不超过 O(p log p)，其中，p 是跟踪窗口的像素数量。

    In this section, we discuss the components of filter based trackers. Section 3.1 discusses preprocessing performed on the tracking window. Section 3.2 introduces MOSSE filters which are an improved way to construct a stable correlation filter from a small number of images.Section 3.3 shows how regularization can be used to produce more stable UMACE and ASEF filters. Section 3.4 discusses the simple strategy used for the online update of the filters.

      本小节中，我们详细讨论滤波器的组成部分。 3.1小节讨论在追踪窗口上的预处理。3.2小节介绍 MOSSE 滤波器，它是一种改进的方法，可以从少量的图像序列中构建一个稳定的滤波器。 3.3小节展示了如何使用正则化项去产生更稳定的 UMACE 和ASEF 滤波器。 3.4小节简要介绍在线更新滤波器的策略。

3.1 Preprocessing

    One issue with the FFT convolution algorithm is that the image and the filter are mapped to the topological structure of a torus. In other words, it connects the left edge of the image to the right edge, and the top to the bottom.During convolution, the images rotate through the toroidal space instead of translating as they would in the spatial domain.Artificially connecting the boundaries of the image introduces an artifact which effects the correlation output.

    This effect is reduced by following the preprocessing steps outlined in [3]. First, the pixel values are transformed using a log function which helps with low contrast lighting situations. The pixel values are normalized to have a mean value of 0.0 and a norm of 1.0. Finally, the image is multiplied by a cosine window which gradually reduces the pixel values near the edge to zero. This also has the benefit that it puts more emphasis near the center
of the target.

3.1 预处理

      快速傅里叶变换的一个问题就是，图像和滤波器被映射到一个圆环的拓扑结构上，也就是说，它将图像的左边缘和右边缘相连接，上边缘和下边缘相连接。在卷积过程中，图像的旋转是在超环面中进行的，而不是在空间域。人为的连接图像边缘会影响相关输出。

      这种影响可以通过文献3提出的方法进行消除。首先，使用一个 log 函数对像素进行转换，有助于应对低对比度照明。这些像素值被归一化：均值为0，标准差为1 。最后，将图像乘以一个余弦窗，逐渐将图像边缘的像素值减小为0.这还有一个好处就是，将更多的重点放在目标的中心位置。

3.2 MOSSE Filters

    MOSSE is an algorithm for producing ASEF-like filters from fewer training images. To start, it needs a set of training images fi and training outputs gi. Generally, gi can take any shape. In this case, gi is generated from ground truth such that it has a compact (σ = 2.0) 2D Gaussian shaped peak centered on the target in training image fi. Training is conducted in the Fourier domain to take advantage of the simple element-wise relationship between the input and the output. As in the previous section, we define the upper case variables Fi, Gi and the filter H to be the Fourier transform of their lower case counterparts.

      

where the division is performed element-wise.

    MOSSE 算法可以从较少的训练样本中，产生类似于ASEF的滤波器。首先，它需要一系列训练图像 fi 和训练输出 gi，一般而言，gi 可以取任何形状。在这种情况下，gi 是从 ground truth 中生成的，因此，在训练图像的目标物体上，会产生一个非常紧凑的标准差为 2 的 2D 高斯尖峰。训练是在傅里叶域中进行，是为了利用输入和输出之间的对应关系。和上一小节一样，我们定义了 Fi,Gi,和滤波器 H ，对应小写字母 f,g 的傅里叶变换。

                         （2）

其中，除法是对应元素相除。

    To find a filter that maps training inputs to the desired training outputs, MOSSE finds a filter H that minimizes the sum of squared error between the actual output of the convolution and the desired output of the convolution.This minimization problem takes the form:

            （3）

    The idea of minimizing Sum of Squared Error (SSE) over the output is not new. In fact, the optimization problem in Equation 3 is almost identical to optimization problems presented in [10] and [12]. The difference is that in those works it was assumed that the target was always carefully centered in fi and that the output (gi) was fixed for the entire training set, whereas customizing every gi is a fundamental idea behind ASEF and MOSSE. In the tracking problem the target is not always centered, and the peak in gi moves to follow the target in fi. In a more general case gi can have any shape. For example, in [4] fi contains multiple targets and gi has multiple corresponding peaks.

      为了找到一个能将训练输入集合映射到期望的输出集合的滤波器。Mosse 发现了滤波器 H ，通过这种方式：最小化实际输出的卷积和期望输出的卷积之间的差的平方和。最小化问题的公式如下：

      

    最小化输出的误差平方和也不是啥新的概念。事实上，对于上面那个公式的优化问题几乎和文献 10 和 11 中提到的方法相同。不同之处在于，那些方法中，在整个训练集上，目标总是处于输入 (fi) 的中心，输出（gi）总是固定的。其中每个 （gi）都是定制的，这也是 ASEF 和 MOSSE背后的基本思想。在跟踪问题上，目标不一定始终处于中心位置，在 gi 中的峰值也会随 fi 中的目标移动。更多情况下，gi 可以是任意形状的。例如在文献4中， fi 包含多个目标，gi 有多个响应峰。

    Solving this optimization problem is not particularly difficult but does require some care because the function being optimized is a real valued function of a complex variable. First, each element of H (indexed by  and ロ) can be solved for independently because all operations in the Fourier domain are performed element-wise. This involves
rewriting the function in terms of both Hロ and H.ロ. Then, the partial W.R.T. H.ロ is set equal to zero, while treating Hロ as an independent variable [13].

      

By solving for H∗ a closed form expression for the MOSSE filter is found:

  （5）

    A complete derivation is in Appendix A. The terms in Equation 5 have an interesting interpretation. The numerator is the correlation between the input and the desired output and the denominator is the energy spectrum of the input.

      解决这个优化问题并不是很难，但是需要注意一些东西，因为这个优化的函数是一个复杂多变的实值函数（即值域为实数，不可为负数）。首先，H （下标以w,v来表示。注：计算机里面，数字图像的坐标系为 uwv）中的每个元素，都可以被单独处理，因为在傅里叶域，所有的操作都是对应元素相运算的（比如说对应元素相乘，对应元素相除等）.这就需要重写 ，然后，当将作为一个独立变量时，关于的一部分要设置为 0。

          （4）

而 H* 的求解可以近似表达成下面形式：

        （5）

      附录 A 有完整的推导。而对于上面的公式（5），有一个有趣的解释。分子是输入和期望输出之间的关系，分母是输入的能谱.

    From Equation 5, we can easily show that UMACE is a special case of MOSSE. UMACE is defined as H. = D.1m. where m is a vector containing the FFT of the average centered cropped training images, and D is a diagonal matrix containing the average energy spectrum of the training images [18]. Because D is a diagonal matrix, multiplication by its inverse essentially performs an

    To show that MOSSE produces better filters than ASEF, an experiment was conducted which varied the number of images used to train the filters. The filters were initialized by applying random small affine perturbations to the tracking window for the first frame of the video.The PSR on the second frame was used as a measure of filter quality. Figure 3 shows that MOSSE produces better filters when trained on a small number of image windows.
The reason will be discussed in the next section.

      从公式 5 中我们可以看到，UMACE 是 MOSSE 的特殊情况（此处是介绍 UMACE 的，就不翻译了，了解一下，看懂就行。）

      为了显示MOSSE 能产生比 ASEF 更好的滤波器，我们进行了一个实验：改变图像的数量，用来训练滤波器。通过在视频中的第一帧中，在追踪窗口上应用一个小的仿射变换，来初始化滤波器。在第二帧中使用 PSR 去衡量滤波器的好坏。图 3 显示了 MOSSE 可以利用较少的图像窗口，训练出更好的滤波器。这个原因会在下一节给出。

3.3 Regularization of ASEF

    ASEF takes a slightly different approach to minimizing error in the correlation transformation. It turns out that when there is only one training image Fi and one output image Gi, there is a filter that produces zero error. That filter is called an exact filter and can be found by solving Equation 1:

    An exact filter trained on one image will almost always overfit that image. When applied to a new image, that filter will often fail. Averaging is used to produce a filter that is more general. Motivation for averaging comes from Bootstrap Aggregation [5] where the output of weak classifiers can be averaged to produce a much stronger classifier. With some manipulation, the equation for an ASEF filter can be shown to be:

If only one image is used for training, MOSSE and ASEF both produce an exact filter.

     在相关性转换时，ASEF 采取了一个稍不同的方法去最小化偏差。当仅仅只有一帧训练图像 Fi 和一个输出图像 Gi ，会产生一个零偏差的滤波器。这个滤波器被称为精确的滤波器，它可以通过求解 公式1 获得。

             （7）

      在一帧图像上训练滤波器，往往会过拟合。当应用于新的一帧图像时，那个滤波器经常就失效了。产生更一般的滤波器的方法，就是求平均值（averaging）。求平均的灵感是来自于文献5中提出的引导聚类：输出的许多弱分类器通过平均，产生一个更强的分类器。通过一些推导， ASEF 的公式可以被描述为：

          （8）

如果是只利用一张图像来训练， MOSSE 和 ASEF 都可以产生很精确的滤波器。

    ASEF filters are unstable when trained on small numbers of images because the element-wise division in Equation 8 becomes unstable when a frequency in the training image contains very little energy (or the denominator is close to zero). Averaging large numbers of exact filters compensates for this problem and produces robust ASEF filters. Because the denominator for MOSSE is the sum of the energies over more images, it will rarely produce small numbers and is therefore more stable. 

    Alternatively, regularization can be used to correct for low-energy frequencies and produce more stable ASEF filters. This is performed by adding a small value to each element in the energy spectrum. The Fi ⒘ F. i is replaced with Fi ⒘ F. i + . where . is the regularization parameter. 

    Regularization is similar to a result that came from OTF theory which is typically used in conjunction with UMACE filters. This result suggests that adding the energy spectrum of the background noise to that of the training imagery will produce a filter with better in noise tolerance [16]. Here we have essentially added white noise. 

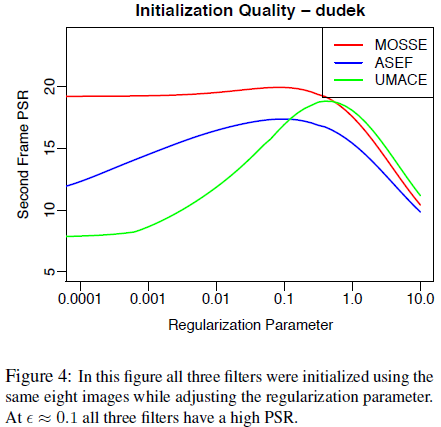
    Figure 4 shows the effect of adjusting .. With proper regularization all of the filters are producing good peaks and should be stable enough to produce a good track.

      当训练样本集的图像个数比较少时， ASEF 是不稳定的。因为当训练图像的频率包含较小的能量（或者分母非常接近 0），公式 （8）中对应元素相除就变得不稳定了。大量精确的滤波器进行平均能够弥补这个问题，从而产生鲁棒的滤波器。因为 MOSSE 的分母是很多图像的能量之和，它几乎不会产生较小的数字，所以，是更稳定的。

      或者，正则化可以用来校正低能频率，产生更稳定的 ASEF 滤波器，这是在能谱中给每个元素加上一个小的值，也就是， 变成了，其中是正则化参数。

      正则化的效果和 UMACE 滤波器和OTF 理论相结合的结果是很相似的。这一结果表明，将背景的能谱增加到训练图像中，可以产生抗噪能力更强的滤波器。其实，实际上，我们增加的是白噪声。

      图 4 显示了调节  的影响，通过正则化，所有的滤波器都将产生较好的峰值，而且足够稳定，能够产生较好的追踪轨迹。

      

3.4 Filter Iniialization and Online Update

    Equations 8 and 5 describe how filters are constructed during initialization. The training set is constructed using random affine transformations to generate eight small perturbations (fi) of the tracking window in the initial frame.Training outputs (gi) are also generated with their peaks corresponding to the target center.

    During tracking, a target can often change appearance by changing its rotation, scale, pose, by moving through different lighting conditions, or even by undergoing nonrigid deformation. Therefore, filters need to quickly adapt in order to follow objects. Running average is used for this purpose. For example, the ASEF filter learned from
Frame i is computed as:

and the the MOSSE filter as:

where η is the learning rate. This puts more weight on recent frames and lets the effect of previous frames decay exponentially over time. In practice we have found that η = 0.125 allows the filter to quickly adapt to appearance changes while still maintaining a robust filter.

      公式 8 和公式 5 描述了在初始化过程中滤波器是如何被构造的。训练集是这样被构造的：使用仿射变换在初始帧中生成 8 个追踪窗口的小扰动（fi），训练输出 gi 的产生是通过与目标中心相对应的峰值。

      在追踪过程中，目标经常会改变外观，比如旋转、尺度、姿态、光照，甚至通过非刚性变换。利用平均值就是为了解决此类问题。比如，从第 i 帧图像中学习 ASEF 滤波器可以这样被计算；

           （9）

MOSSE 滤波器：

其中，η 是学习率。这给最近的一些帧增加了一些权重，并且，之前的若干帧对滤波器的影响，是随着时间的推移呈指数式衰减。实际上，我们在实践中发现，η = 0.125，能让滤波器快速适应目标外观的变化，同时也能保证滤波器比较鲁棒。

3.5 Failure Detection and PSR

    As mentioned before a simple measurement of peak strength is called the Peak to Sidelobe Ratio (PSR). To compute the PSR the correlation output g is split into the peak which is the maximum value and the sidelobe which is the rest of the pixels excluding an 11 × 11 window around the peak. The PSR is then defined as gmax.μsl σsl where gmax is the peak values and μsl and σsl are the mean and standard deviation of the sidelobe.

      如之前提到的，衡量峰值强度的一个简单方法叫做 PSR : 峰值旁瓣比。为了去计算 PSR ，

整体理解与部分函数：

相关滤波的思想：越是相关的两个目标相关值越大，也就是视频帧中与初始化目标越相似，得到的相应也就越大。卷积定理：时域的卷积相当于频域相乘，频域卷积相当于时域相乘。

本论文目标就是找到一个滤波器h，使其在目标上的响应最大。f表示训练图像，g表示输出图像，h表示滤波器，F，G，H对应其频域值。

1、为了简化计算，将时域的卷积转化为频域的点乘积。

时域公式表示：

频域公式表示：

 

所以目标H的计算为：

 

2、MOSSE又叫输出的平方差误差最小滤波器。

滤波器的目标函数：

 

可得到H的闭式解为：

3、MOSSE更新方法：

4、部分代码

%产生高斯形状的理想响应

F_response=templateGauss(target_sz,im);

%目标框区域和滤波器卷积得到响应值

newPoint=real(ifft2(F_Template.*fft2(target_box)));

%其中响应值最大值对应的坐标即为新目标的位置

[row, col,~] = find(newPoint ==max(newPoint(:)), 1);

%以新目标为中心选择目标框

F_im=fft2(getsubbox(pos,target_sz,im));

%求解滤波器模板

F_Template=conj(F_im.*conj(F_response)./(F_im.*conj(F_im)+eps));