题目:
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5 L 1234567890 [email protected] N 1234567890 [email protected] N 1234567890 [email protected] L 1234567890 myQQ@qq L 1234567890 [email protected]心得体会:
这道题就是让我们对输入的QQ号与库中的数据进行比对,这其实就是按要求做查找,
但是由题目可知,输入的命令行数最多为十万行,
即极端情况下需要对数据量达到十万的数据进行查找,
且Q号为一个不超过10位、但大于1000的整数,
无论是顺序查找、折半查找还是树表查找都无法实现或效率不高,
这时候我们可以考虑一下散列表查找
首先我们先定义散列表的结构
struct qq
{
string key; //判断是否为空
long long int num;//QQ号
string code;//密码
}; //散列表结构
然后是构造散列函数,这里我直接使用了除留余数法,
因为输入QQ号最多为十万个,所以取稍大于十万的质数100019
int getkey(long long int x)
{
return x % y;
}//取关键字
接下来是处理冲突方法,这里直接选择线性探测法
查找思路为:
①判断该单元是否为空
②
若为空则跳出循环,表中无该QQ号
若不为空则比较输入QQ号与该单元下存储的QQ号是否相同
③
若相同则返回该关键字
若不相同则将key+1再取模,继续搜索
int search(long long int num)
{
int key;//关键字
key = getkey(num);//取关键字
while (Hash[key].key == "key")
{
if (num == Hash[key].num)
return key;
else(key=(key+1)%y);
}
return -1;
}//散列表查找
依次写出creat和login函数
void creat(long long int qq, string code)
{
int flag = 0;//该Q号创建状态
if (search(qq) == -1 && flag == 0)//散列表中无该QQ号且该Q号创建状态为0
{
int key;
key = getkey(qq);
while (flag == 0) //寻找空余单元格存储Q号
{
if (Hash[key].key != "key"&& flag == 0)
{
flag = 1;
Hash[key].key = "key";
Hash[key].num = qq;
Hash[key].code = code;
cout << "New: OK" << endl;
}
if (Hash[key].key == "key"&& flag == 0) key = (key + 1) % y;
}
}
if (search(qq) != -1 && flag == 0)//散列表中已有该Q号
{
cout << "ERROR: Exist" << endl;
flag = 1;
}
}
void login(long long int qq, string code)
{
if (search(qq) == -1) cout << "ERROR: Not Exist"<
完成这些函数后,整个问题就迎刃而解了
目标完成情况:
上次目标算是完成了吧,对图的理解与运用能力有所提高
下次目标:
好好复习,把前面所学的知识都回顾一遍
融会贯通,好好准备期末考
附:关于B+树B-树区别
转载自:伯乐专栏作者/玻璃猫,微信公众号 - 梦见 漫画:什么是b+树
一个m阶的B树具有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
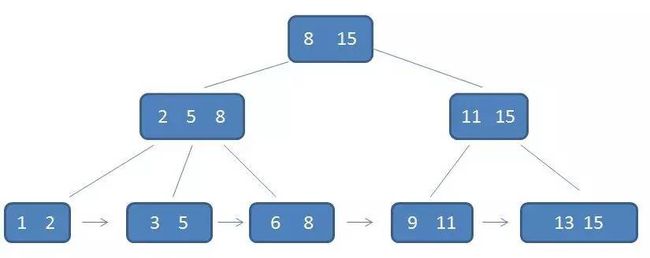
一个m阶的B+树具有如下几个特征:
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
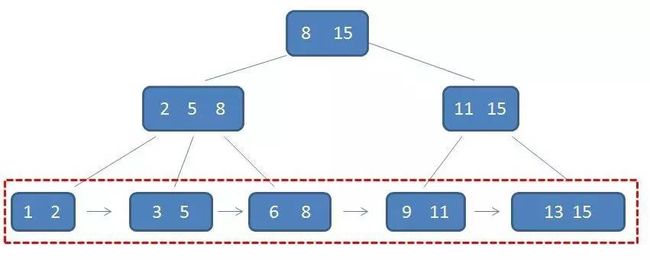
2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
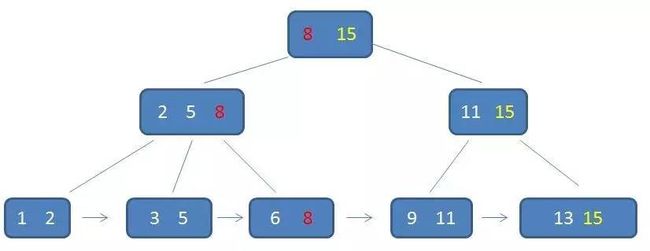
3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
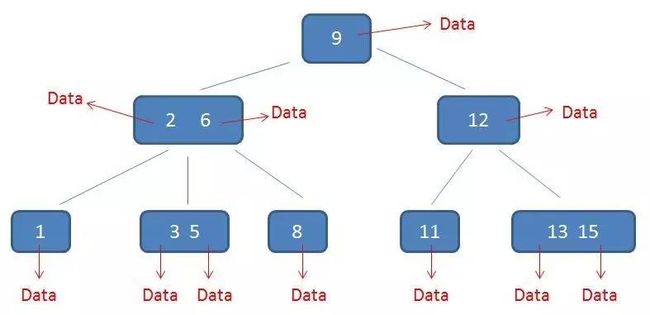
B-树中的卫星数据(Satellite Information):
B+树中的卫星数据(Satellite Information):
需要补充的是,在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
第一次磁盘IO:
第二次磁盘IO:
第三次磁盘IO:
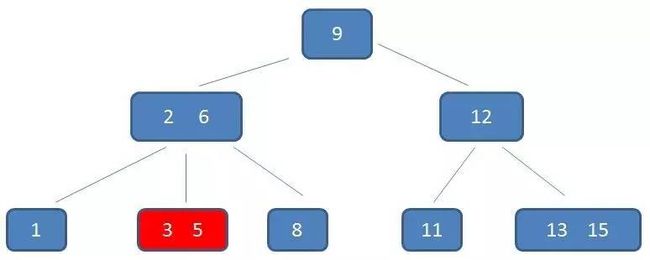
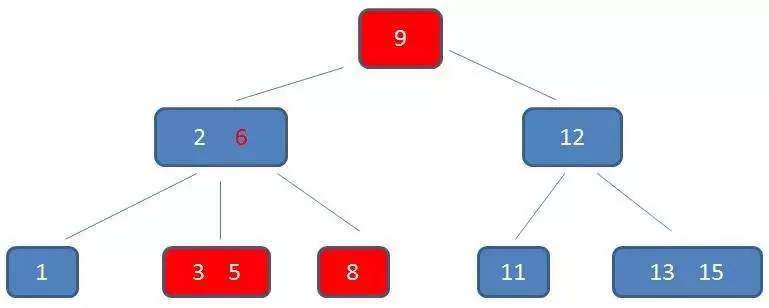
B-树的范围查找过程
自顶向下,查找到范围的下限(3):
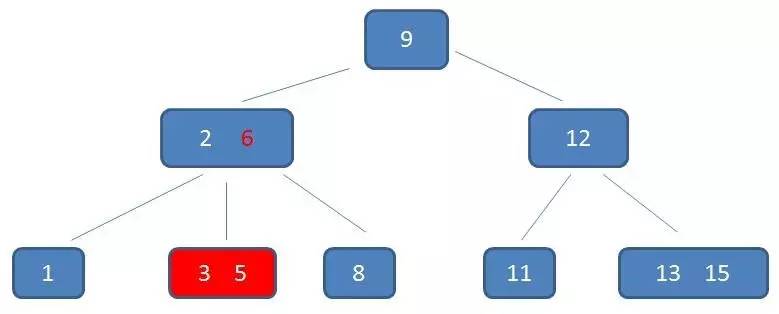
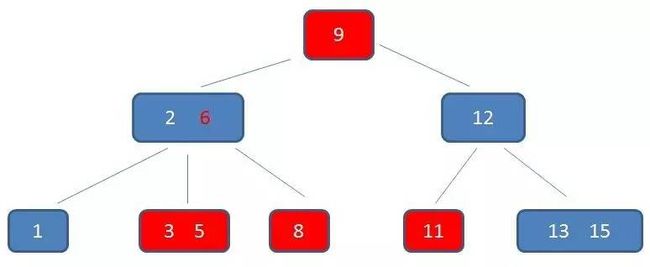
中序遍历到元素6:
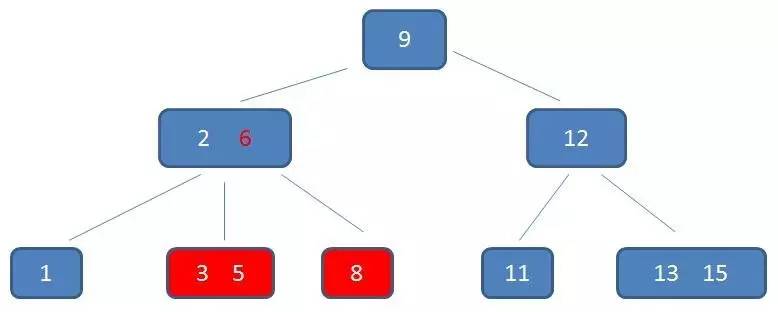
中序遍历到元素8:
中序遍历到元素9:
中序遍历到元素11,遍历结束:
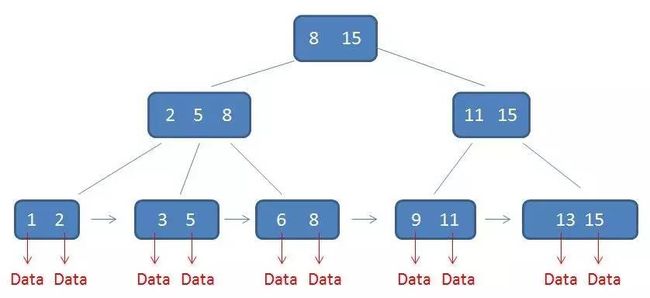
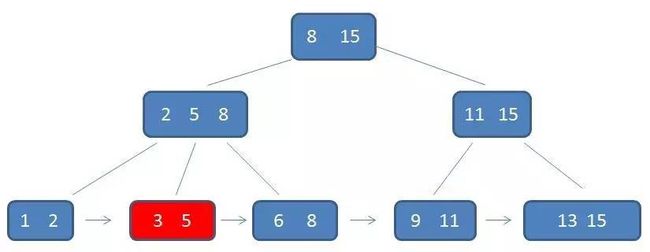
B+树的范围查找过程
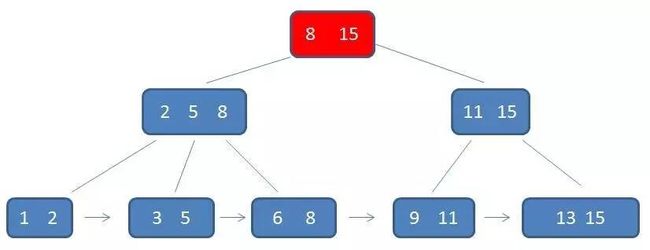
自顶向下,查找到范围的下限(3):
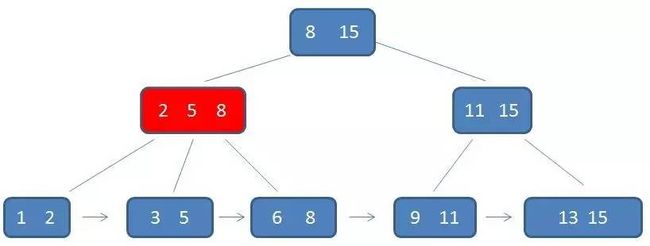
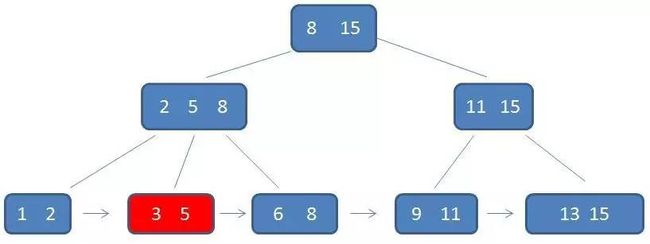
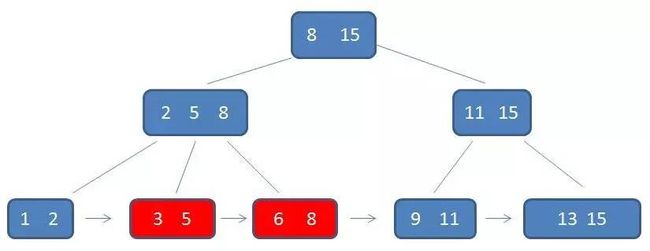
通过链表指针,遍历到元素6, 8:
通过链表指针,遍历到元素9, 11,遍历结束:
B+树的特征:
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
B+树的优势:
1.单一节点存储更多的元素,使得查询的IO次数更少。
2.所有查询都要查找到叶子节点,查询性能稳定。
3.所有叶子节点形成有序链表,便于范围查询。