python 数据降维PCA，KernelPCA模型

运行环境：win10 64位 py 3.6 pycharm 2018.1.1

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold

def load_data():
    iris = datasets.load_iris()
    return iris.data,iris.target

#首先使用PCA类
def test_PCA(*data):
    X,y = data
    pca= decomposition.PCA(n_components=None)
    pca.fit(X)
    print('explained variance ratio : %s :'% str(pca.explained_variance_ratio_))
X,y = load_data()
test_PCA(X,y)

#给出绘制样本分布图的函数
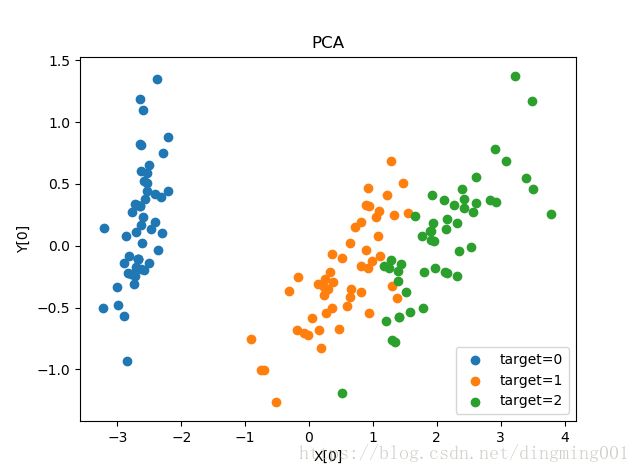
def plot_PCA(*data):
    X,y = data
    pca = decomposition.PCA(n_components=2)
    pca.fit(X)
    X_r = pca.transform(X)
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    for label in np.unique(y):
        position = y == label
        #此处position表示是否打印出来，True与False
        ax.scatter(X_r[position,0],X_r[position,1],label='target=%d'%label)
    ax.set_xlabel('X[0]')
    ax.set_ylabel('Y[0]')
    ax.legend(loc='best')
    ax.set_title('PCA')
    plt.show()

X,y = load_data()
plot_PCA(X,y)

#超大规模的数据降维
decomposition.IncrementalPCA

#KernelPCA
#测试各个核函数
def test_KPCA(*data):
    X,y = data
    kernels= ['linear','poly','rbf','sigmoid']
    for kernel in kernels:
        kpca = decomposition.KernelPCA(n_components=None,kernel=kernel)
        kpca.fit(X)
        print('kernel=%s --> lambdas:%s:'%(kernel,kpca.lambdas_))
X,y = load_data()
test_KPCA(X,y)

#给出绘制降维后样本的分布图的函数：
def plot_KPCA(*data):
    X,y = data
    kernels = ['linear','poly','rbf','sigmoid']
    fig = plt.figure()

    for i,kernel in enumerate(kernels):
        kpca = decomposition.KernelPCA(n_components=2, kernel=kernel)
        kpca.fit(X)
        X_r = kpca.transform(X)
        ax = fig.add_subplot(2, 2, i+1)
        for label in np.unique(y):
            position = y == label
            ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label)
            ax.set_xlabel('x[0]')
            ax.set_ylabel('x[1]')
            ax.legend(loc='best')
            ax.set_title('kernel=%s'% kernel)
    plt.suptitle("KPCA")
    plt.show()
X, y = load_data()
plot_KPCA(X, y)

# 考察多项式核的参数影响，给出测试函数
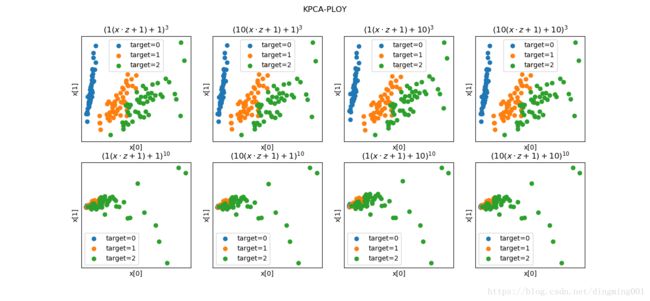
def plot_KPCA_ploy(*data):
    X, y = data
    fig = plt.figure()
    params = [(3,1,1),(3,10,1),(3,1,10),(3,10,10),(10,1,1),(10,10,1),(10,1,10),(10,10,10)]
    for i,(p,gamma,r) in enumerate(params):
        kpca = decomposition.KernelPCA(n_components=2,kernel='poly',gamma=gamma,degree=p,coef0=r)
        kpca.fit(X)
        X_r = kpca.transform(X)
        ax = fig.add_subplot(2,4,i+1)
        for label in np.unique(y):
            position = y == label
            ax.scatter(X_r[position,0],X_r[position,1],label='target=%d'%label)
            ax.set_xlabel('x[0]')
            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_ylabel('x[1]')
            ax.legend(loc='best')
            ax.set_title(r'$(%s(x\cdot z+1) + %s)^{%s}$'%(gamma,r,p))
    plt.suptitle('KPCA-PLOY')
    plt.show()
X, y = load_data()
plot_KPCA_ploy(X, y)

#考察高斯核参数的影响
def plot_KPCA_rbf(*data):
    X, y = data
    fig = plt.figure()
    gammas = [0.5,1,4,10]
    for i,gamma in enumerate(gammas):
        kpca = decomposition.KernelPCA(n_components=2,kernel='rbf',gamma=gamma)
        kpca.fit(X)
        X_r = kpca.transform(X)
        ax = fig.add_subplot(2,2,i+1)
        for label in np.unique(y):
            position = y == label
            ax.scatter(X_r[position,0],X_r[position,1],label='target=%d'%label)
            ax.set_xlabel('x[0]')
            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_ylabel('x[1]')
            ax.legend(loc='best')
            ax.set_title(r'$\exp(-%s||x-z||^2)$'%gamma)
    plt.suptitle('KPCA-RBF')
    plt.show()
X, y = load_data()
plot_KPCA_rbf(X, y)

#考察sigmoid核的参数的影响
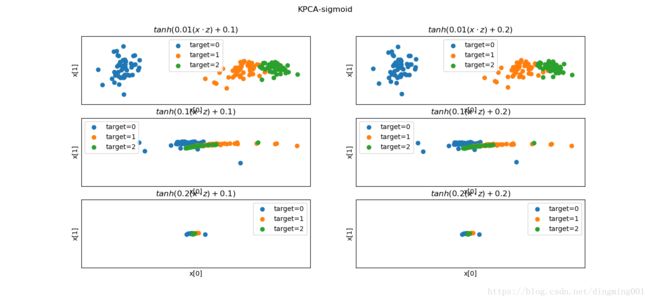
def plot_KPCA_sigmod(*data):
    X,y = data
    fig = plt.figure()
    params = [(0.01,0.1),(0.01,0.2),(0.1,0.1),(0.1,0.2),(0.2,0.1),(0.2,0.2)]
    for i,(gamma,r) in enumerate(params):
        kpca = decomposition.KernelPCA(n_components=2,kernel='sigmoid',gamma=gamma,coef0=r)
        kpca.fit(X)
        X_r = kpca.transform(X)
        ax = fig.add_subplot(3,2,i+1)
        for label in np.unique(y):
            position = y == label
            ax.scatter(X_r[position,0],X_r[position,1],label='target=%d'%label)
            ax.set_xlabel('x[0]')
            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_ylabel('x[1]')
            ax.legend(loc='best')
            ax.set_title(r'$tanh(%s(x\cdot z)+%s)$'%(gamma,r))
    plt.suptitle('KPCA-sigmoid')
    plt.show()

X, y = load_data()
plot_KPCA_sigmod(X, y)