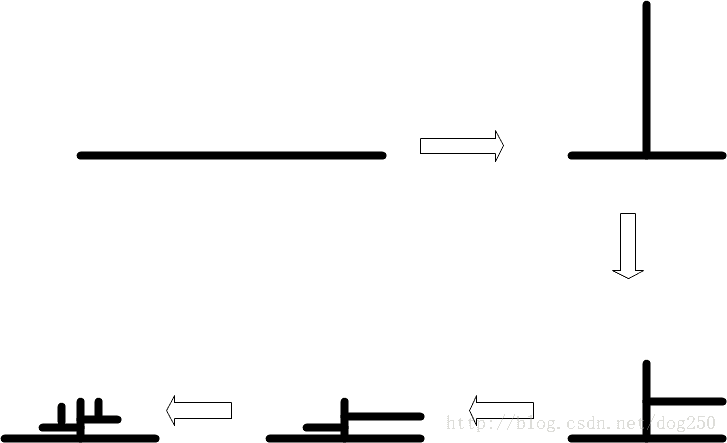根号2以及π的计算--关于无理数的畅想

曾经写过两篇用朴素的原始思想理解现代数学概念的文章：
《科普文章-另一个视角解读计算机编码(修订版)》
《原始人的除法引发的闲聊》
这两篇文章里，我发现不需要那些老师教的范式也能很好地理解那些现代概念，并且理解的更深刻。我一般假设自己从来没有学过微积分，没有学过高等代数，只有初中水平，把自己放在古人的位置上，看看如何从本质上理解现代数学概念(当然，虽然古人在知识的丰富程度上不如我们，但他们中的很多人在逻辑思维方面是碾压我们现代大学生的，比如欧几里得，毕达哥拉斯他们)，这个过程带来往往不仅仅是快感。
  今天是看完《三体：地球往事》的第二周，脑子一直烧到现在根本停不下来，所以今天写这篇文章发泄一下，作为下周继续看第二部开张前的引子。

引

本文以计算两个无理数 2√ 和π开始，引出无理数的橡皮筋模型的烧脑旅程。以下的 2√ 和π的计算都是我自己想出来的，按照一贯的做法，我算出来后又核对了一下典籍，看看标准的做法怎么算，发现了惊人的一致，这说明了朴素的方法可能真的很少，如果能找到，那必然会找到一样的，我试着忘掉所有学过的那些高等数学知识，去解这类问题，每当我一想到泰勒级数，积分这些，就直接pass掉，最终我真的用朴素的初中二年级掌握的概念解决了问题。…..然而我老婆说我背下了从书上看的结论，这绝对是冤枉啊，要是背结论一篇文章能憋一周吗？我写的东西里很少有那些结论性的总结性的东西(比如说虽然我精通Netfilter和iptables，但至今没有一篇手册性的文章…)，几乎都是自我有感而发，我觉得只有这样才最真实。更可况，我一个大专生在本科退学前就上过一年半的基础课，哪能学那么多高尚的知识。此后我就成了一个网管，再也没有时间去研究基础学科了，哭惨…
  写这篇文章，和别的文章不同，我花了比较久的时间，喝着真露，听着各种版本的《成都》…

行文之前有个声明，本文的内涵在于朴素地解释问题，我知道我将要说的这些都有严密的数学论证，但是我的重点在于，尽量绕开那些让人头疼的论证让人理解事情的真相。真相往往是简单的。

2√ 如何计算

要想了解事情的真相，必须从本源入 2√ 手。
  我知道 2√ 的求法有很多种，刚学过微积分的趁着还没有忘记时可能倾向于用级数展开的方式求解，刚学过编程的趁着还没有忘记时则可能会采用二分法求解，然而对于一个初中生，你指望他怎么算 2√ 呢？当然，我们记得，在上初中的时候，老师曾经在黑板上演示过他的老师教给他的竖式来手工计算开方，这也算一种方法，虽然只用到了乘除法但却不朴素，更像是背口诀的方法，所以也被我放弃。
  我这里采用的是最朴素的欧几里得辗转相除法计算 2√ ，整个过程非常简单，几乎是一气呵成。

1.定义问题

首先，我们定义问题，如下图所示：

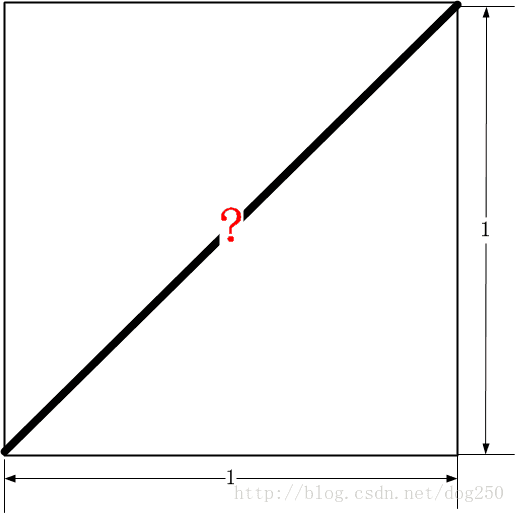
问题就是已知正方形边长为1，求对角线的长度。

2.找几何关系

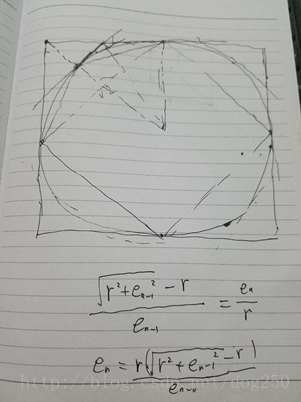
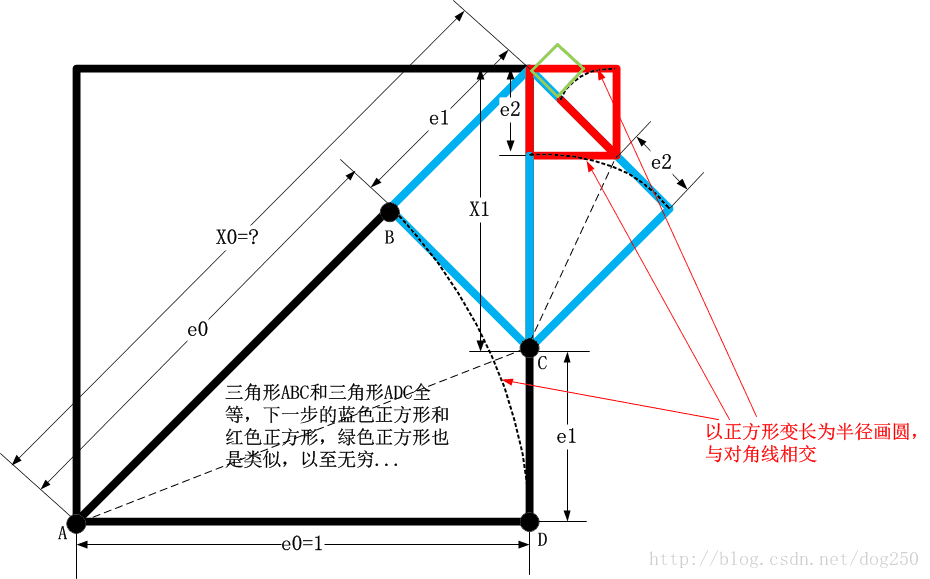
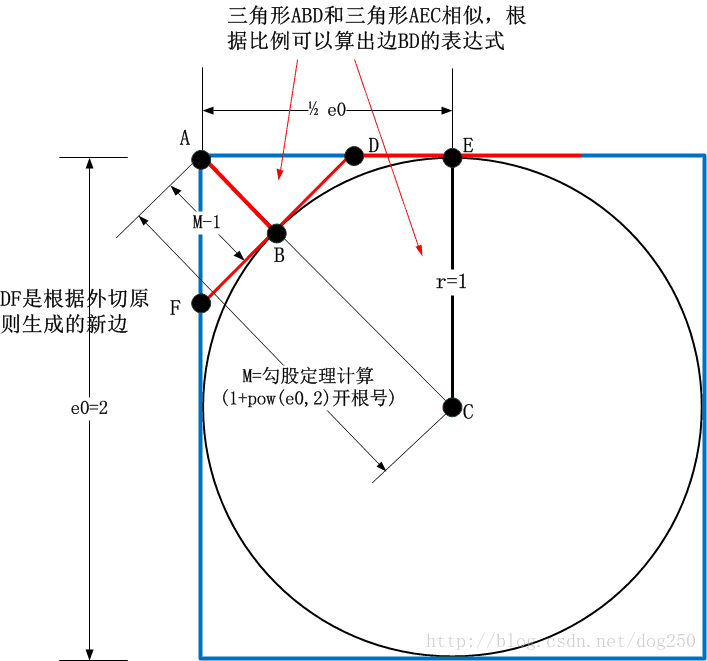
接下来就是找关系，如下图所示：

仅仅从图上，我们就已经可以看得出一种明显的循环递推关系了，接下来就是用代数式子将这种几何关系写出来。顺便说一句，上图中的几何关系并非我原创，它的思想来自欧几里得的《几何原本》，我只是用它做了别的用途，我不用它来证明 2√ 是无理数，而是用它来求 2√ 本身。

3.整理并推导代数关系

中学的一个物理老师告诉我，要想得到美妙的结论，必须有大段大段整理数学式子的能力。求解 2√ 的数学式子不复杂，量也不大，但还是有一些的。把上节中的几何关系用式子表达出来就是：

x0=e0+e1
x1=e1+e2=e0−e1 —> 2e1+e2=e0
x2=e2+e3=e1−e2 —> 2e2+e3=e1
x3=e3+e4=e2−e3 —> 2e3+e4=e2
…

为了能更好地将变量集中起来，来对每一个式子做一个除法：

x0e0=1+e1e0
x1e1=1+e2e1=e0e1−1 —> 2+e2e1=e0e1
x2e2=1+e3e2=e1e2−1 —> 2+e3e2=e1e2
…

好的，到此为止，我们已经可以发现一个明显的关系了，即前一个式子的尾项的倒数可以通过后一个式子表示，我们逐式子代入…
  为了行文结构更加明显，我用单独的一节来导出结论。

4.导出结论

接着上一节，我直接将尾项用后一个式子代入，得到一个无穷尽的式子：

e0=1

x0e0=1+12+12+12+12+12+...

显然，这是一个永远都结束不了的代入过程，结束不了的原因从上面的几何关系就能看出，所有切割出来的小正方形跟老的正方形都是相似形，边长和对角线的关系是不会变的。
  正因为这种无穷无尽，就是说没有办法用一个有限步骤的操作来表达 2√ 这个数，它虽然明明确确就在那里，却无法用有限步骤的操作去描述它，描述它的式子虽然无穷尽，却尽然美妙，这带来的是一种幸福感还是一种悲伤的心情…

附：另一个递推关系

我附上在推导过程中导出的另一个关系，虽然这个关系无法直接用于计算 2√ ，但却也是十分规整美妙的。
  如果在上述推导过程中没有对式子做除法进而集中变量，我们便得到明显的尾项倒数关系这个结论，只能将某一个自变量单独代入下一个式子，从而得到下面的式子：

x0=e0+e0−e1−e2−e3−e4−e5−e6−...2222222

本节的结束就是计算 2√ 的结束，你可以动笔算一下，后面的式子拖的越长，结果就越精确。不想动笔算的，可以用下一节我给出的计算机程序来让计算机代算。

5.验证代码

本节给出一个代码，其意义仅仅用来代替纸笔计算，算法依赖的式子就是上面推导出来的那个结论，这并不是程序自己会推导那个式子，是我告诉程序的，程序只是个执行者而已。

#include 

static int accuracy = 0;
static int paccuracy = 0;
static long double param;

long double calc(long double result)
{
        long double ret;
        accuracy ++;
        if (accuracy > paccuracy) {
                return result;
        }
        return calc(1/(2 + result));
}

void main(int argc, char **argv)
{
        paccuracy = atoi(argv[1]);
        param = 2;

        printf("%.15Lf\n", 1 + calc(1/param));
}

6.计算的背后

熟悉数学的可能一眼就能看出我上面的那个结论就是大名鼎鼎的 2√ 连分数表示，然而虽然结论相同，其推导过程却是显然不同的，我们知道， 2√ 的连分数表示是通过解类似下面的方程的根推导出来的：

x2+x=3

或者说是显式的辗转相除法纯代数推导出来的，然而我这里却是通过几何关系导出的，最终指向了同一个结论。
  我们仔细观察最后的那个连分数式子：

x=1+12+12+12+12+12+x

其背后是不是还有点二分法逼近的意思呢？虽然不是二分，却带有逼近的意思，我们看一个独立式：

x=1+12+12+x

第二个比第一个小一点，第三个又比第二个大一点…
  好吧，关于无理数的含义和逼近的意义，这里必须打住，在深入聊这个话题之前，我再来演示一下圆周率π怎么计算

π如何计算

和 2√ 的计算一样，π也可以用级数展开求解，然而本文并不描述那种“大学生的方式”，本文依然回归朴素的本质，看看古人是怎么求解π的。
  提到π，都能想到的一个人是祖冲之，就因为他是中国人，所以中国人很多人为了展示或者炫耀自己的记忆力，都会去背π，然而没有人去背 2√ …
  其实，在数学方面，西方要强大得多，但因为我个人就是研究希腊罗马近东的，所以为了避嫌就不说西方多么优秀了，本文我以魏晋时期刘徽的割圆术为基底，重现一下当年是怎么用朴素的手段算π的。和 2√ 的计算一样，朴素的方法思路都是一致的，所以不存在谁抄谁的问题。思路依然是自己在一个下了班的回家路上一气呵成的。

1.割圆术

这个概念不想多说，请自行百度。我在求解π之前，其实并不知道割圆术这个名词，也是后来才百度的，我只知道古人的思路就是如此，并不知道是刘徽创立的，其实现在我也不信是他创立的，难道春秋战国时期造轮子不用π吗？虽然早就有“径一周三”一说，然而那样造出来的战车得多么颠簸啊…我觉得早就刘徽之前很久，人们就知道π的计算了，刘徽只是总结了一套Howto而已，后面的祖冲之在刘徽的Howto指导下Step by step提高了精度，仅此而已。
  重要的是什么？重要的是古人怎么发现圆的周长和半径之间的关系的，怎么发现它们的比值是一个常数，这是关键，至于常数是多少，那纯粹是一个计算问题，是一个工程问题。
  我这里给出我的猜测，我觉得轮子是一个伟大的发明，原始人或者新石器时代的人没有闲工夫去算一些没有现实意义的抽象的东西，他们造轮子是因为轮子可以更快捷地运输，轮子的意义堪比弓箭，古人在造轮子的时候自然会发现π。
  本文中，我纠结的是，到底是从正四边形开始，还是从正六边形开始，都是很美丽的多边形…最后我选择了正四边形，因为我爱垂直胜过爱对称，不知道怎么回事。

开篇

2.找出几何关系-内接多边形

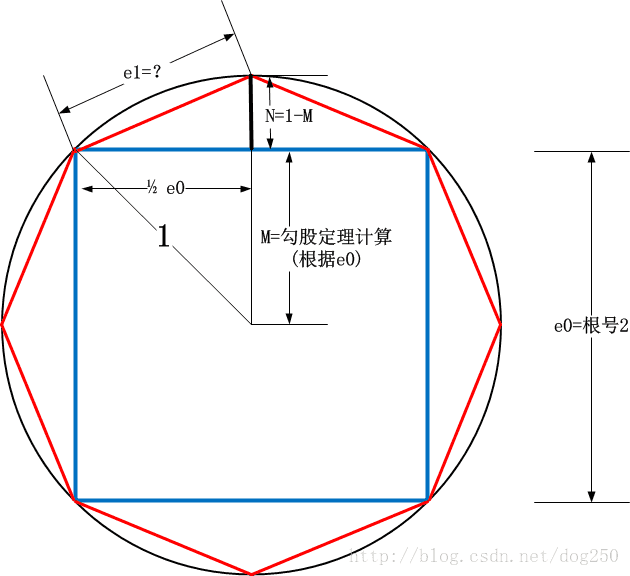
正四边形接下来就要分割为正八边形，然后是正十六边形，我们分割试试看，试图找出一些关系：

很简单不是吗？直接就用勾股定理搞定了，有点落差感，我本来是想动用全等，相似，比例的，好久没有折腾几何，现在搞起来真的仿佛回到了中学时期。

3.导出代数关系-内接多边形

代数递推关系非常简单，直接给出结论吧：

en=(en−12)2+(1−en−12−−−√)2−−−−−−−−−−−−−−−−−−√

按照这个递推关系，任意增加边数，算出来的周长就越接近2*π。
  计算π的过程本该结束了，然而其实还有另外一个方法计算π。如果说用内接多边形计算是从左边逼近π的话，那么用外切多边形则是从右边逼近π，这个正是我马上要演示的。

4.找出几何关系-外切多边形

我们现在看圆的外切多边形如何进一步分割逼近圆周。和内接多边形一样，我们还是要找出关系：

和内接多边形不同的是，外切多边形逼近圆周稍微复杂一点，不光用到了勾股定理，还用到了相似形比例。还好这些都是初中水平的东西，还算朴素。

5.导出代数关系-外切多边形

代数递推关系也不难，只是跟内接多边形逼近相比，稍微复杂那么一点点，还好，在计算量上都是一致的：

r=1

r+e2n−1√−ren−1=enr=en

6.结论和代码

我们有了上面的内接多边形和外切多边形的计算方案后，就可以下结论说π的值介于内接多边形周长和外切多边形的周长之间(当然这个周长要乘以一个系数，其实就是1/2)，于是乎，π的计算方法就很明显了，就是用上述两个递推公式，把π的区间逼的越来越小，由于手算的能力有限，我就直接上代码了：

#include 
#include 

static int accuracy = 0;
static int paccuracy = 0;
static long double param;

long double calc_inscribed(long double e)
{
        long double a, b, ne;
        accuracy ++;
        if (accuracy >= paccuracy) {
                return e;
        }
        a = pow(e/2, 2);
        b = pow(1 - sqrt(1 - pow(e/2, 2)), 2);
        ne = sqrt(a + b);
        return calc_inscribed(ne);
}

long double calc_circumscribed(long double e)
{
        long double a, b, ne;
        accuracy ++;
        if (accuracy >= paccuracy) {
                return e;
        }
        a = sqrt(1 + pow(e, 2)) - 1;
        b = e;
        ne = a/b;
        return calc_circumscribed(ne);
}

void main(int argc, char **argv)
{
        long double e = sqrt(2);
        long double pi1, pi2;
        int n = 4, paccuracy2;
        paccuracy = atoi(argv[1]);

        pi1 = pow(2, paccuracy+1)*calc_inscribed(e)/2;
        accuracy = 0;
        pi2 = pow(2, paccuracy+1)*calc_circumscribed(1);
        printf("%.15Lf  < Pi < %.15Lf\n", pi1, pi2);
}

把这个代码编译运行，不过几秒钟，然而古人没有计算机，他们只能手算，接下来你可能会问，怎么手算开方，噢，这是另一个问题，古人肯定是有办法的，顺便说一句，中国人在手算开方方面是绝对碾压西方的。

7.猜测祖冲之是怎么确定π的区间的

这还用猜吗？
  如今祖冲之计算圆周率的方法早已失传，可能是由于那个战乱的年代….(我有十足的欲望从数学扯到游牧民族入侵，进而扯到罗马帝国…但精力不允许)只是留下来个结论，他把π的值压缩到了 3.1415926 和 3.1415927 之间，且问他是怎么做到的？
  我猜测他就是用内接多边形和外切多边形夹逼得到的区间，而这个区间的宽度是他那个年代的极限。惊人的结论是，现代计算机用long double型都达不到那个精度…所以我惊奇的不是祖冲之算出了几，而是他到底是怎么算的。

二分法开方

这一节纯粹是多余的，因为二分法这是最常用的开方方法，见多了就不觉得美妙了，所谓的黑科技一般都是第一眼看上去就亮瞎了眼的东西。为了表明自己是个程序员，所以只是给出代码：

#include 
#include 

static int accuracy = 0;
static int paccuracy = 0;
static long double param;

long double sq(long double x) 
{
        long double low = 0, high = x, mid;
        while (low <= high) {
                accuracy ++;
                if (accuracy >= paccuracy) {
                        break;
                } 

                mid = (low + high) / 2;
                if (mid * mid == x) {
                        high = mid;
                        break;
                }
                else if (mid * mid < x)
                        low = mid;
                else
                        high = mid;
        }
        return high;
}

void main(int argc, char **argv)
{
        long double n = atoi(argv[2]);
        paccuracy = atoi(argv[1]);

        printf(" %.15Lf\n", sq(n));
}

无理数畅想

现在开始扯无理数。后面的篇幅为酒后之作，我特意在没有喝酒的情况下写完了上面的部分，因为计算需要严谨。然而下面的部分需要豪放，必然要喝点酒的。

  无理数到底是什么？无理数和有理数相比哪个更多？…

数轴是什么

首先我们看一下数轴，按照我们常规的想法，数轴上的每一个数字都是按照大小在数轴上排排坐的，一个挨着一个，如下图所示：

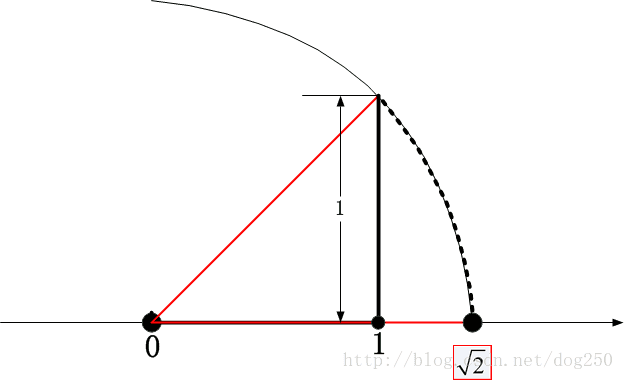
这也是毕达哥拉斯学派的观点，他们认为所有的数字都是可以在数轴上精确定位的，世间万物的关系最后归结到一条数轴。然而有一日有一人构造出了一个数轴上的点：

请问， 2√ 在数轴上的坐标是什么？
  本文前面的部分我们可以看到， 2√ 是无法用有限的步骤表示的，也就是说，我们没有人知道它到底是多少，然而数轴上的点却是一个确定的点，这显然是矛盾的事实啊！怎么办？不管怎样，在古代真的有人为此付出了生命的代价。
  数轴如果说是一个刚体，我们永远无法解释上面的矛盾，我们确认能构造出一个固定的确定的点，然而这个点的坐标却是未知的(因为它的值不可计算)，很烧脑吧…
  我猛然想到了《三体》中的那两个质子。是的，就是那两个质子。三体世界举国上下进行的实验场景时时刻刻萦绕着我。一个一维的点展开后竟然会是一个世界，所以我试着沿着这个思路解释数轴。显然找到了一个合理的答案。
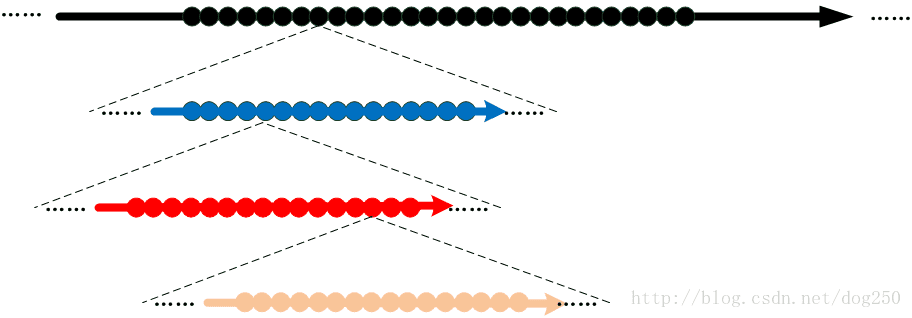
  数轴是一根无限长并且在任意一点可以无限伸展的橡皮筋！这意味着无限延展的数轴上任意一点都是可以无限展开的：

我来简单解释一下。
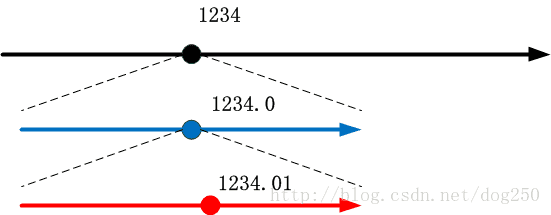
  我们定义一个十进制数X，它有n位，每一位都属于一个维度，以四位数为例，比如1234，那么这显然是处在四维空间的数：

• 第一维：数值为4，表示“1”维度；
• 第二维：数值为3，表示“10”维度；
• 第三维：数值为2，表示“100”维度；
• 第四维：数值为1，表示“1000”维度。

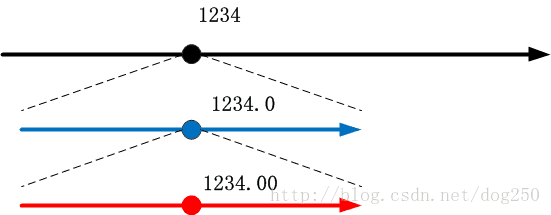
那么数轴上1234.00怎么表示呢？很显然，将1234所在的坐标点展开，
再展开两个维度即可：

注意，数轴上每一个维度都是一个和上一个维度完全一样的一根数轴，是不是有点分形的意思呢？
  虽然说1234和1234.00是相等的，但是在数轴上表示所需的维度却完全不同，我们说1234.00是一个六维数字，而1234仅仅是四维数字。进一步，我们看一下1234.01怎么表示：

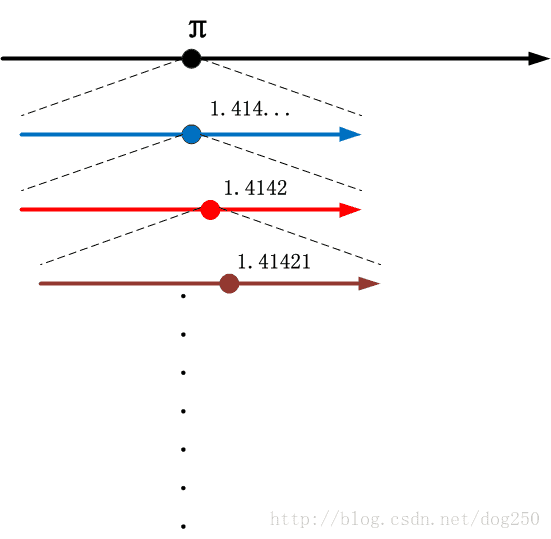
循着这个思路，我想 2√ 怎么表示就已经真相大白了，从最初的1.414开始，按照上面的图示，逐步向下沉，以至无穷…：

总结一下吧，数轴是一个多维度的坐标系，而不是像我们往常认识到的那样是一维的。如果一个数字用有限的维度可以表示，即不用沉到不见底的深渊就可以表示的那种数，那么这种数就可以用其每一个维度的坐标连接在一起表示就好了，比如1234,1234.00,1000,3.1415926…然而像那种必然无法用有限伸展步骤表示的数，比如 2√ ，π之类，就只能用一些奇奇怪怪的符号的来表示了，这种数就是所谓的无理数。
  当 2√ 铡刀铡下来的时候，在数轴上打中的一颗三体世界的质子，这颗0维的质子展开后就是一个多维的世界，一个无穷尽的世界。
….
以上就是我对数轴的理解，这个模型包含了所有的数字，那些所谓的有理数只是恰好从其数值的最后一位代表的维度一直到无穷的最后一个维度的分量同时为0而已，试想如果上帝随机创造了所有的数字，这种无限维坐标系中无限维度分量同时为0的概率是多么的低！
  爱因斯坦不相信上帝在掷骰子，然而事实上上帝说不定真的在掷骰子，上帝在祂的世界可能只是一个三流赌徒，可能毫无逻辑可言，祂带给我们这个世界的所谓“逻辑”或许仅仅是巧合。有位朋友说过，一个有理数2，对应多个无理数，比如 2√ ， 2√3 ， 2√4 …
  说实话，在想出这个基于分形理论的橡皮筋数轴模型前，我听到过“空隙”数轴模型，说的是有理数并没有布满整个数轴，而是中间有看不见的空隙，这些空隙里塞满了无理数，然而基于这个模型，我很难想象如何去比较有理数和无理数的多少，而这个问题在分形橡皮筋模型里却很容易理解，有理数和无理数其实处于两个世界，在通往无理数的过程中，不管走了多远，只要停止，那么就100%被确认为有理数，只有一直走下去的数才是真正的无理数。

两个隔离的世界

你可以无限地趋近于她，却无法可达，这是一种多么无助的悲哀…就像质子和电子。一想到这个，我就突然感到一阵伤感。
  上帝的世界和我们的世界是两个世界，我们的世界和计算机游戏里的世界也是两个世界，不管多么接近，永远也无法融为一体，甚至不能相互比较。有理数和无理数也是处在两个世界，有理数处在有限的世界，而无理数则是处在无穷的世界，两个世界里，比较谁多谁少是没有意义的，虽然感官上我们总觉得有理数多一些，但是一想到无穷这个概念，我们显然无助了，人类的思维在超过三维的世界里显得十分无能为力。
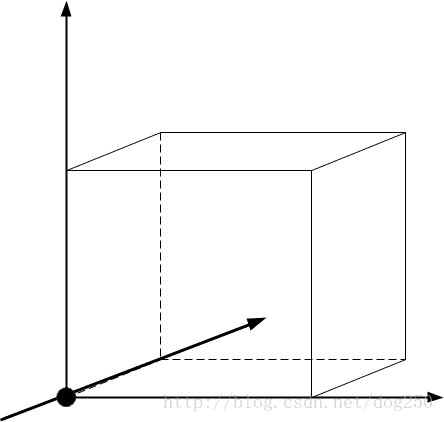
  如果上帝真的掷骰子，并且祂真的就是天真的牌手，我觉得祂创造出无理数的概率要远大于有理数。我用下面的图示作为本节的总结和下一节的开始：

假设在没有重力的环境里，你往一个立方体里扔球，球恰好落在壁上的概率有多大呢？

如何逼近一个无理数

当我们理解了无理数是一个什么概念后，按照数轴上的点不断展开的原则，我们可以不断逼近一个无理数，虽然永远都不可能到达，但却可以无限地逼近它，每展开一个维度，我们便天真地认为我们离那个无理数更近了，然而这是我们对无穷的误解，无穷带来的只有无情。
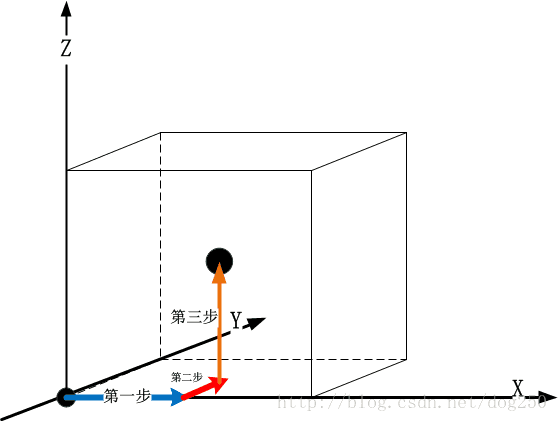
  按照下图，我们来看一下如何到达一个立方体的核心：

很显然，先沿着X轴走边长的一半，然后沿着Y轴走边长的一半，最后沿着Z轴走完边长的一半，到达核心。其实逼近一个无理数也是这么玩的。说逼近而不是到达是因为无理数的维度是无穷维度的，也就是永远没有最后一步！所以说只能逼近。按照削平果的方法，其实逼近过程是很简单的，先沿着1轴，再沿着2轴，然后接连3轴，4轴，….不断逼近。这个思路和无穷级数的思路非常类似，我们可以把级数展开的每一项都看成一个维度即可。

多维树匹配

早在2014年，我玩过一个叫做nf-HiPAC的东西，里面集成了一个多维树匹配算法，可以快速匹配数据包，而不再像传统iptables那样逐条线性匹配，从而大大提升了网络处理的性能。
  其实逼近一个无理数的过程和这个是非常类似的。关于多维树匹配的细节，我写过下面这篇文章：
《HiPAC高性能规则匹配算法之查找过程》
我们在nf-HiPAC机制对一个数据包的匹配过程中可以看到一个类似逼近无理数的过程。
  在研究nf-HiPAC的时候，我曾经关注过K-D树搜索算法，其实我觉得逼近一个无理数的方法和K-D树搜索算法非常相似。我们都很熟悉无穷级数，比如泰勒级数和傅立叶级数，它们都可以表示成一系列的项的加和，如果把每一个项看作是一个维度上的分量，那么整个无穷项的西格玛表示正是表示了一个数字无穷维度向量本身。

分数和小数以及无理数的表示法

按照以上我对数轴和无穷维度空间的解释，分数和小数之间的关系就很显然了。
  小数可以看作将一个数展开后的表示，比如1展开后就是1，1/2展开后就是0.5， 2√ 展开后就是1.41421…，1/3展开后就是0.333333…我们发现，对于很多的数字，不得不用省略号来替代后面无穷无尽的无法精确表达的部分，这显然是有缺陷的表示，为了表示数本身，就需要采用另一种表示法，即分数，然而无理数又无法用分数表示，就只能用一些奇奇怪怪的符号表示了，比如π， n√ ，ln之类。

三体质子与大肠

在我读完《三体》第一部之后，质子多维展开让我真的难以忘怀，后来我想了很久，试图用一种简单朴素的方式去理解它，一直到我的橡皮筋数轴模型出炉(该模型我会用严谨的数学去描述，然而并不适合发布在博客上了)，我方才可以从里到外一气呵成地解释整件事情。
  先说说大肠吧，据说一段大肠要把肠壁展开，可以铺满200平方米，比大多数人家的房子都大很多，你能想象一脬屎住的房子有那么大吗？一脬屎住在200平米的房子里，然而这200平米的房子住在你的身体里，而你可能只是租住在不到50平米的房子里…这好像有点矛盾，到底哪里出了问题？
  过年时去了川西的青藏高原东缘，我尽可能把地图放大，然后非常精确地测量了318国道沿途从当天出发地到目的地的距离，试图估算一下到达时间。然而几乎每次行驶的实际距离和测量距离都是谬之千里，甚至有数倍的差异，为什么100公里变成了200公里？不合理啊！后来我找到了答案，我在地图上看到的路径是这样子的：

然而实际的路径却是这样子的：

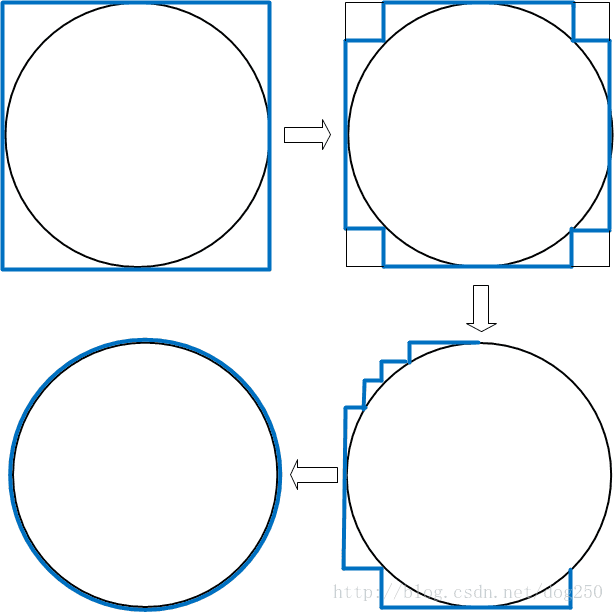
朴素点说，一个维度确实可以藏在另一个维度里，并且藏得还挺深。我用一个错误的割圆术来说明问题：

看到了吧，假设圆的半径是1，经过上述的过程，一个周长为8的正方形，成功地变成了周长为2*π的圆形，剩余的那(8-2*π)的长度哪里去了？
  论证这个可能需要复杂的数学，一般人都会望而却步，但是我这里可以给出一个感官上可以直达的解释。有人会说，长度压缩了，宽度必然增加，然而并不是，道理很简单：

一个方向增加宽度，另一个方向减小，趋向于不增加。
  那么，事实上的结论就是，长度就是压缩了，没有伴随宽度的增加。越来越烧脑了，长度差到底去哪了？！！
  当我们纠结于这个静态的矛盾的时候，我们忽略了一个动态的过程，说白了就是我们缺失了一部分信息！这里隐藏了信息，那就是这个圆生成的过程！如果仅仅给出一个圆，你不知道它是橡皮筋做成的还是刚体做成的，要想知道这个信息，就必然要知道这个圆生成的过程，这显然是一个重要的信息。
  你无法从一个东西的当前状态去判定它的性质，你必须要了解它的历史状态(比如男人眼里的女人，或者女人眼里的男人或女人)，这就必然要把时间维度考虑在内！长度隐藏在了时间维度里！
  延展到多维度，直至无穷维度，像无理数这种，真的可以压缩到一个零维度的质子里面，只要不断的把信息压缩进上一维度即可，一直到最后，变成一个点！
  回到现实，时间可以冲淡一切，也可以压缩一切。
  有什么不对吗？好吧，我承认，这不是学霸想要的答案，但却是任何一个喜欢思考的人想听的答案，想得到严谨数学论证的请私聊我，还好我在2003年寒冷的哈尔滨研究过一段时间分形学。
  要知道，整个毕达哥拉斯的数的理想世界，竟然是一个分形的世界，不知古人知道了这个会有多么伤感啊。他们所能理解的所谓有理数，竟然是分形数轴上中了头彩的上帝的骰子掷下的结果，十分罕见！我们假设上帝的骰子是无穷面的，祂连续无穷次投掷，按投掷时间的结果依次是：1，0，2，4，0，0，0，0，…(后面全是0)，上帝纵然万能，也是个赌徒，这概率得有多么低！
  有理数和无理数哪个多呢？这取决于上帝是一个什么样的赌徒。
  本节的最后总结一句，数轴本来就是分形的轮盘，上帝参赌。

杂论

已经是晚饭后了，我继续这篇文章的最后部分。

1.镜像

昨晚，我问老婆和小小，什么是无限接近但却永远不可达的，我想找一个现实中的模型。老婆的回答让我觉得非常不错，答曰镜子，你照镜子的时候就会体会。

2.π的意义

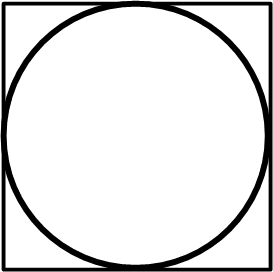
有人提出可以用随机数的概率来计算π，具体方法呢就是往下面的图形围成的范围里随机撒沙粒：

最后数数落在整个范围内的沙粒数量和仅仅落在圆形范围里的沙粒数量的比值，就可以算出π了，大自然是不会骗人的，是吗？

  这个招数很妙！然而能不能反过来用呢？即用π来检测随机数的质量。

3.再谈橡皮筋

一条橡皮筋能隐藏多少信息？数轴上的一个点可以无限被拽的要多长有多长，拽出来的都是有理数，永远拽不出的才是无理数，就好像从一个黑洞往外拽东西，都会变成无限长(任何东西被黑洞吸收时都会变成无限长，被拽出来时也一样)，然而怎么理解无限？拿有理数和无理数比较数量，我感觉像是在宇宙拿星球和黑洞比数量，然而谁又能看一眼黑洞？这就像生与死的两个世界。在有理数的世界，你甚至不能内窥一眼无理数的概念，因为一旦你看到了就再也无法与这个世界联络。除非我们找到一个同时囊括这两个世界的主的世界，否则，任何比较都没有意义。
  都没有意义！必须升维。

4.现代数学

经过中世纪之后，特别是笛卡尔，牛顿之后，数学从一个模糊的领域独立成了一个基础学科，此后的数学开始持续迅猛发展，这些话看上去尽是套路…
  我自己觉得，数学不好玩了，它已经从一种思辨术堕落成了一种演算术，这就像自由格斗堕落成了拳击比赛或者散打比赛一样，后者一定没有前者好看。数学少了思辨，更多的是在一个演绎系统内部按照特定的规则进行运算，你可以把这些规则理解成公式，或者口诀都行，但至于这些规则从何而来，很少有人关注，我反而觉得这才是最有意思的。
  现代数学自文艺复兴后开始，就几个有意思的东西，一个是微积分，另一个是黎曼几何，集合论也算一个，其它的都是小丑，都是工程性的东西，试想，一个高中天天背诵的应试教育者考上了大学，被老师灌输了一大堆公式，然后该学生拿着这一大堆公式去解一些毫无意义的方程式，这有意思吗？
  现代数学在现代教育理念的影响下，会解题往往被认为数学水平高，貌似学数学就是为了解题，而不是为了解释现象。