导出离散傅里叶变换（DFT）的两种方法

1. 原理部分

  在这里首先确定DFT的对象为一个有限长的离散非周期序列，这主要因为计算机处理的都是有限长的离散序列。如果你要处理的序列本身不是离散非周期的序列，可以通过截取或者离散化等方法获得所需的有限长的离散非周期序列。

  对于有限长的离散非周期序列存在两种计算N点DFT的方法，一种方法是先将其通过DTFT获得序列的连续周期的频谱，取其中一个周期进行N点抽样即可得到DFT；另一种方法直接由 x(n) 计算N点的DFT，但是这种方法要求 DFT 变换的点数 N 大于等于原始时序序列的点数。下面将给出一个具体的例子进行说明。

2. 举例说明

  题目

   x(n)=R16(n) ，求 N 分别取8，16,32,64时的离散傅里叶变换DFT X(k) ，并利用反变换求各个频谱对应的时序序列，比较这些频谱和序列。

  第一种方法：直接计算

  这种方法的原理在于首先将时序序列进行以 N 为周期的周期延拓，然后取出其中的一个周期计算在 k=0:N−1 上的DTFT（注意原始的是计算 k∈(−∞,+∞) )。要如果计算DFT的点数大于等于时序序列本身的点数，那么不通过周期延拓直接计算就好，因为周期延拓之后后面的都是补上的０，没有计算价值，因为计算完也是０。这时的计算公式如下

X(k)=ΣN−1n=0x(n)e−j2πNnk=ΣN−1n=0x(n)WknN,k∈[0,N−1]

但是！这里可以直接使用 x(n) 进行计算是因为 x(n) 以 N 点为周期进行周期延拓后面补的都是0，算不算这些点都没有什么关系，但是像这个问题，本身 x(n) 是一个16点的矩形序列，如果做 8 点的DFT时首先要以 8 为周期进行周期延拓，延拓后序列在时域上有混叠，所以不能直接将 x(n) 代入上式进行计算，应该带入周期延拓之后时序序列的进行计算。但是这样做明显太麻烦了，这时就需要第二种方法了。

  第二种方法：由 DTFT 导出 DFT

  这种方法是首先计算序列的 DTFT，再取一个周期进行 N 点抽样。这种方法是符合DFT原始定义的方法的一种导出形式，无论是计算多少点数的DFT变换均可以，而且在变换的过程中也不需要进行补零操作。

3. 代码实现

  本代码运行环境为 MATLAB 2014a

3.1 直接计算法

  具体的计算思想可以参见从 DTFT 的角度用矩阵相乘代替 for 循环进行计算。

clc;clear all;close all;

%% 绘制x(n)
x = ones(1,16);n=0:15;
subplot(5,2,[1,2]),stem(x);

%% x(n)的DTFT
w=0:2*pi/3200:2*pi;
Xdtft0=x*exp(-1i*n'*w);
subplot(5,2,3),plot(w/pi,abs(Xdtft0));

%% x(exp(jw))的IDTFT
syms ww
Xdtft=x*exp(-1i*n'*ww);
Xidtft = int(Xdtft*exp(1i*ww'*n),ww,-pi,pi)/2/pi
subplot(5,2,4),stem(Xidtft);

%% x(n) 的16点，32点，64点的 DFT & IDFT
NN = [16,32,64];
for N = NN
    nn = find(NN==N)
    nnn=0:N-1;
    k=0:N-1;
    xn = [x,zeros(1,N- 16)]; 
    Xk=xn*exp(-1j*2*pi/N).^(nnn'*k); 
    www = 0:2*pi/N:2*pi;
    subplot(5,2,3+2*nn),stem(www(1,1:N)/pi,abs(Xk));  
    xx=(Xk*exp(j*2*pi/N).^(nnn'*k))/N;
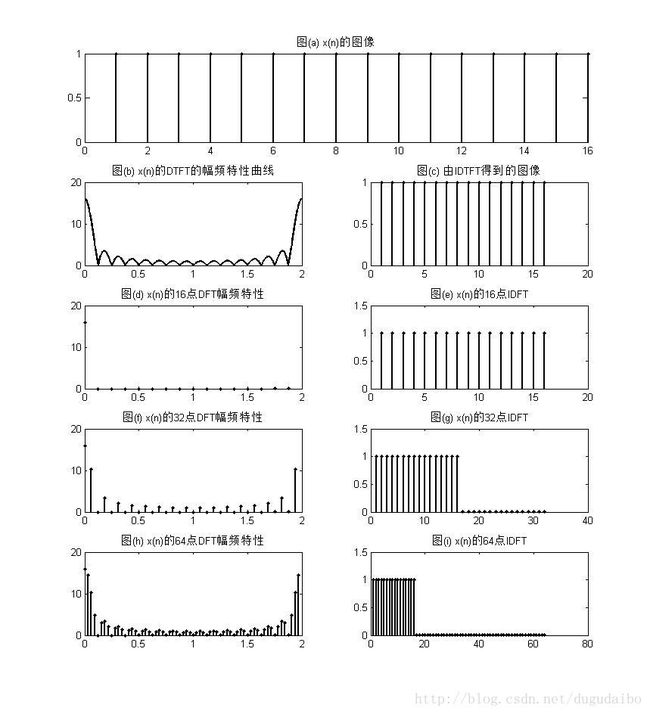
    subplot(5,2,4+2*nn),stem(abs(xx));
end

  实验结果如下图所示

  从图中我们可以清楚的看到，DFT的点数就是对原序列DTFT一个周期内频谱的采样点数。从频率采样定理可以知道，当频域采样点数大于等于时域实际序列的点数时，可完整恢复序列。但是这里需要注意，这里没有计算序列的8点DFT，该部分将在第二种方法中给出。

3.2 由 DTFT 导出 DFT

clc;clear all;close all;

%% 绘制x(n)
x = ones(1,16);n=0:15;
subplot(6,2,[1,2]),stem(x);

%% x(n)的DTFT
w=0:2*pi/3200:2*pi;
Xdtft0=x*exp(-1i*n'*w);
subplot(6,2,3),plot(w/pi,abs(Xdtft0));

%% x(exp(jw))的IDTFT
syms ww
Xdtft=x*exp(-1i*n'*ww);
Xidtft = int(Xdtft*exp(1i*ww'*n),ww,-pi,pi)/2/pi
subplot(6,2,4),stem(Xidtft);

%% x(n) 的16点，32点，64点的DFT & IDFT
NN = [8,16,32,64]
for N = NN
    hang = find(NN==N)
    count = 1;
    nn=0:N-1;
    k=0:N-1;
    for h = 1:round(3200/N):3200;
        DFT(hang,count) = Xdtft0(h);
        count = count+1;
    end
    www = 0:2*pi/N:2*pi;
    subplot(6,2,3+2*hang),stem(www(1,1:N)/pi,abs(DFT(hang,:)));
    xx=(DFT(hang,:)*exp(j*2*pi/N).^(nn'*k))/N;
    subplot(6,2,4+2*hang),stem(abs(xx));
end

  实验结果如下图所示

  观察上图，图中的第一行与第二行与图1中的第一行、第二行图像相同；第三行为通过DTFT的方式导出的8点DFT的幅频特性和由8点DFT反变换得到的时序序列，我们可以看到时序序列的幅值为2，而不是1，且一个周期内只有8个点。产生这样现象的原因就是之前说过的，频域采样的个数（即DFT变换的点数）小于时序序列的点数造成的。

4. 结论

  从上面可以看到，两种方法中第一种方法（直接计算）适用于DFT点数多余时序序列点数的情况，而第二种计算方法（由 DTFT 导出 DFT）可以不限制DFT变换的点数。从理论上讲，第二种方法似乎更好，但是考虑在实际使用中，DFT的点数如果小于时序序列的点数，这样的变换本身也是没有意义的，所以一般也不会计算这样的DFT，所以了两种方法均可以使用。但是为了保险，推荐使用第二种～