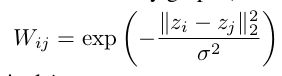《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》阅读笔记
工程地址
课前甜点——使用Jupyter Notebook运行工程中的usage.ipynb
Jupyter Notebook(此前被称为 IPython notebook)是一个交互式笔记本,支持运行 40 多种编程语言。
Jupyter Notebook 的本质是一个 Web 应用程序,便于创建和共享文学化程序文档,支持实时代码,数学方程,可视化和 markdown。 用途包括:数据清理和转换,数值模拟,统计建模,机器学习等等
首先安装一下Jupyter Notebook
pip install jupyter notebook在pycharm打开工程,配置环境
run
Run Jupyter Notebook
控制台上会有一个链接,在浏览器中打开
1:导入自定义文件夹中的函数
源代码中无法import lib下的内容,所以改了一下
import sys
sys.path.append(r'/home/chen/Documents/cnn_graph-master/lib')
import utils
import coarsening
import graph
import models
from lib import models, graph, coarsening, utils
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline2:图的定义和问题定义
n个样本组成了图中的点,每个样本用一个dx向量表示,每个样本xi还有一个标签yi,每个标签可以是离散的label(分类)或者一个dy的向量(回归)表示。点与点之间的权重用一个邻接矩阵A(n*n)表示。这样就可以把一个样本的分类回归问题,理解为图信号分类回归问题。
问题分两种:点的回归分类与图的回归分类。点的回归分类问题:给定矩阵A和n个图信号x,预测图信号y。第二个问题是寻找分类或回归A
3:usage代码解读
from lib import models, graph, coarsening, utils
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline3.1:数据生成
d = 100 # Dimensionality.
n = 10000 # Number of samples.
c = 5 # Number of feature communities.
# Data matrix, structured in communities (feature-wise).
X = np.random.normal(0, 1, (n, d)).astype(np.float32)#生成n*d个(0,1)正态分布的数据,排列成n行d列
X += np.linspace(0, 1, c).repeat(d // c)#生成d个数据,分成c组,组内相同,组间递加。X中每个样本(每行)加上生成的数据
# Noisy non-linear target.
w = np.random.normal(0, .02, d)
t = X.dot(w) + np.random.normal(0, .001, n)#样本各个维度的权重和偏差
t = np.tanh(t)#激活函数
plt.figure(figsize=(15, 5))
plt.plot(t, '.')
# Classification.
y = np.ones(t.shape, dtype=np.uint8)#根据t三分类。
y[t > t.mean() + 0.4 * t.std()] = 0
y[t < t.mean() - 0.4 * t.std()] = 2
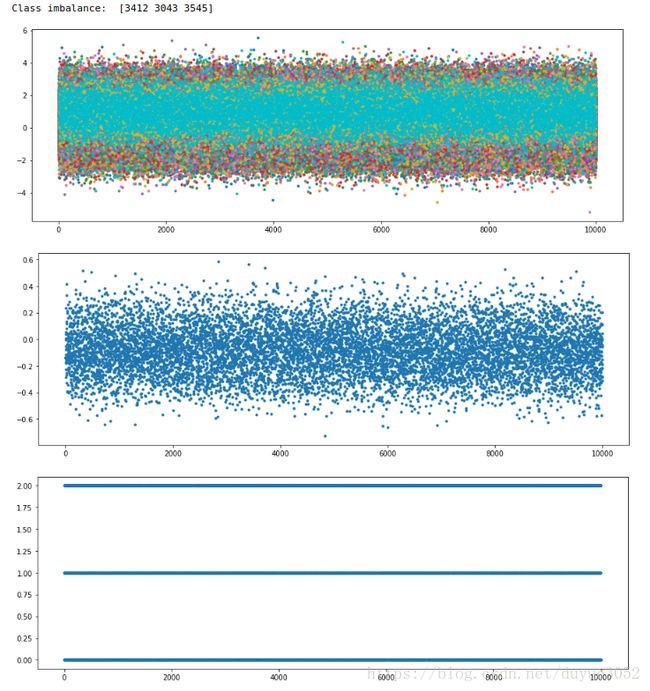
print('Class imbalance: ', np.unique(y, return_counts=True)[1])
n_train = n // 2
n_val = n // 10
X_train = X[:n_train]
X_val = X[n_train:n_train+n_val]
X_test = X[n_train+n_val:]
y_train = y[:n_train]
y_val = y[n_train:n_train+n_val]
y_test = y[n_train+n_val:]从上到下分别是原始数据X(10000,100),特征化后的数据t(10000),标签y(10000)
数据会在coarsening.perm中进行扩展,从100维度变成100+的维度,保持与3.3中生成的L金字塔一致
3.2:图的生成
distance_scipy_spatial函数:
- 计算100维的特征之间的距离矩阵A(100*100的对称矩阵,主对角线=0)
- 返回的是A中每行的最小k个值,以及它对应的A中的下标(可以推断出哪两个特征之间的值)
graph.adjacency函数:
- 计算每个距离的权重:约等于e^-1,距离越大,原始值越小
- 将1000个权重值填充到一个100*100的矩阵中
- 确保是无自环的无向图
dist, idx = graph.distance_scipy_spatial(X_train.T, k=10, metric='euclidean')
A = graph.adjacency(dist, idx).astype(np.float32)
assert A.shape == (d, d)
print('d = |V| = {}, k|V| < |E| = {}'.format(d, A.nnz))
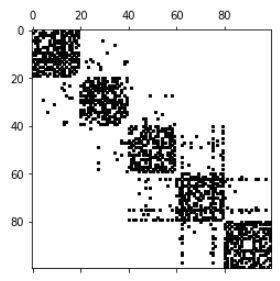
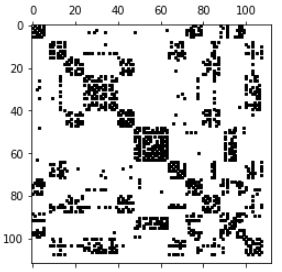
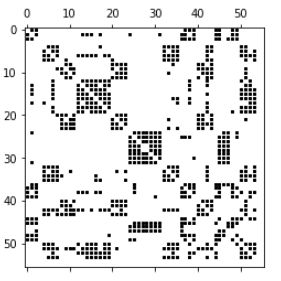
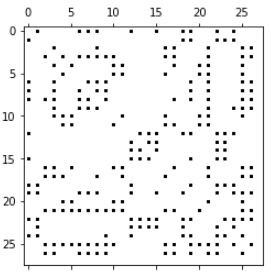
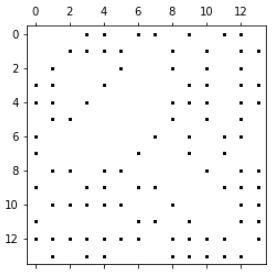
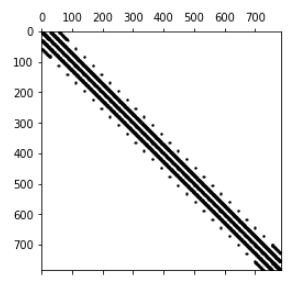
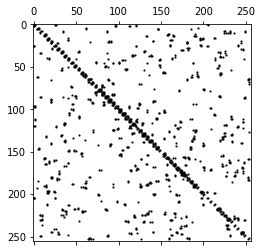
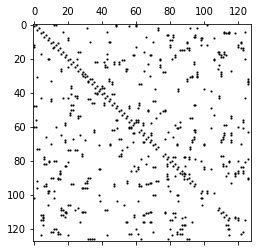
plt.spy(A, markersize=2, color='black');我们来分析一下A是什么样子的,不管之前对x做了什么,对所有样本的每个维度特征影响最大的就:正态分布和分组叠加
最后应该是一个对称矩阵,对角线没有值,组内更可能相同
3.3:图的粗化处理——3层金字塔
coarsening.coarsen函数中大概分两个步骤:- 先用METIS算法做了一个图形粗化
- 然后对每个粗化的图像,做一个上下两层之间关联,所以图像发生形变。
函数返回:如下四个图,以及每个图中每个点的父节点的大小。
graphs, perm = coarsening.coarsen(A, levels=3, self_connections=False)
X_train = coarsening.perm_data(X_train, perm)
X_val = coarsening.perm_data(X_val, perm)
X_test = coarsening.perm_data(X_test, perm)3.4:图的拉普拉斯变换
对每个图做一个拉普拉斯变换,得到与原图像金字塔graphs一样大小的L。L作为网络的输入。
拉普拉斯变换也可以用作边缘检测,用二次导数的形式定义。拉普拉斯变换(Laplace Transform),是工程数学中常用的一种积分变换。
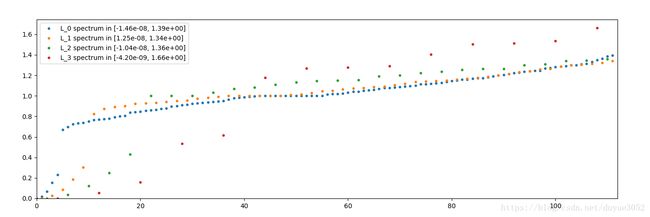
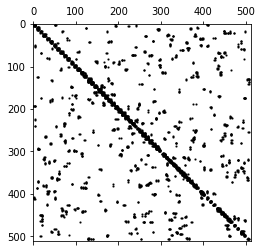
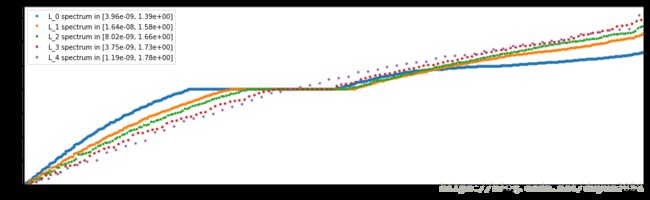
绘制多尺度拉普拉斯L列表的频谱。
L = [graph.laplacian(A, normalized=True) for A in graphs]
graph.plot_spectrum(L)
3.5:网络的构建
网络构建,操作除了卷积使用了3.4节中计算的L外,并没有什么特殊的。包括卷积后的relu,pool,fc都是基本操作。这里核心说一下怎么利用好L做卷积。
两个输入X0和L。一个输出y分成3类。
每个卷积操作中使用L中的一层(两次卷积只使用了两层),图中标注的是第一次卷积的各个矩阵的维度。经过20次的迭代计算后,得到一个输出矩阵,再乘一个可以训练的矩阵w。
params = dict()
params['dir_name'] = 'demo'
params['num_epochs'] = 40
params['batch_size'] = 100
params['eval_frequency'] = 200
# Building blocks.
params['filter'] = 'chebyshev5'
params['brelu'] = 'b1relu'
params['pool'] = 'apool1'
# Number of classes.
C = y.max() + 1
assert C == np.unique(y).size
# Architecture.
params['F'] = [32, 64] # Number of graph convolutional filters.
params['K'] = [20, 20] # Polynomial orders.
params['p'] = [4, 2] # Pooling sizes.
params['M'] = [512, C] # Output dimensionality of fully connected layers.
# Optimization.
params['regularization'] = 5e-4
params['dropout'] = 1
params['learning_rate'] = 1e-3
params['decay_rate'] = 0.95
params['momentum'] = 0.9
params['decay_steps'] = n_train / params['batch_size']
model = models.cgcnn(L, **params)
accuracy, loss, t_step = model.fit(X_train, y_train, X_val, y_val)NN architecture
input: M_0 = 112
layer 1: cgconv1
representation: M_0 * F_1 / p_1 = 112 * 32 / 4 = 896
weights: F_0 * F_1 * K_1 = 1 * 32 * 20 = 640
biases: F_1 = 32
layer 2: cgconv2
representation: M_1 * F_2 / p_2 = 28 * 64 / 2 = 896
weights: F_1 * F_2 * K_2 = 32 * 64 * 20 = 40960
biases: F_2 = 64
layer 3: fc1
representation: M_3 = 512
weights: M_2 * M_3 = 896 * 512 = 458752
biases: M_3 = 512
layer 4: logits (softmax)
representation: M_4 = 3
weights: M_3 * M_4 = 512 * 3 = 1536
biases: M_4 = 3
3.6 Evaluation
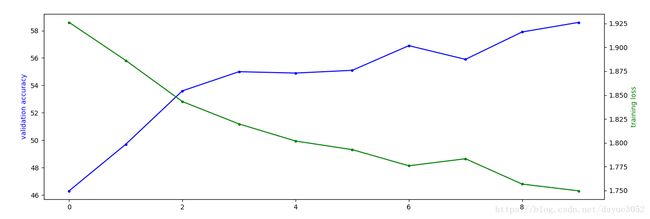
fig, ax1 = plt.subplots(figsize=(15, 5))
ax1.plot(accuracy, 'b.-')
ax1.set_ylabel('validation accuracy', color='b')
ax2 = ax1.twinx()
ax2.plot(loss, 'g.-')
ax2.set_ylabel('training loss', color='g')
plt.show()
print('Time per step: {:.2f} ms'.format(t_step*1000))
res = model.evaluate(X_test, y_test)
print(res[0])4:Mnist上的实验
3中的数据是服从高斯分布的随机数据,接下来我们看看在mnist上的表现,了解怎么把一张图像变成一个图来处理。
import sys, os
sys.path.insert(0, '..')
sys.path.append(r'/home/chen/Documents/cnn_graph-master/lib')
import utils
import coarsening
import graph
import models
import tensorflow as tf
import numpy as np
import time
flags = tf.app.flags
FLAGS = flags.FLAGS
"""
执行main函数之前首先进行flags的解析,也就是说TensorFlow通过设置flags来传递tf.app.run()所需
要的参数,我们可以直接在程序运行前初始化flags,也可以在运行程序的时候设置命令行参数来达到传参的目
的。
"""
# Graphs.
flags.DEFINE_integer('number_edges', 8, 'Graph: minimum number of edges per vertex.')
flags.DEFINE_string('metric', 'euclidean', 'Graph: similarity measure (between features).')
# TODO: change cgcnn for combinatorial Laplacians.
flags.DEFINE_bool('normalized_laplacian', True, 'Graph Laplacian: normalized.')
flags.DEFINE_integer('coarsening_levels', 4, 'Number of coarsened graphs.')
# Directories.
flags.DEFINE_string('dir_data', os.path.join('..', 'data', 'mnist'), 'Directory to store data.')
def grid_graph(m, corners=False):
z = graph.grid(m)
dist, idx = graph.distance_sklearn_metrics(z, k=FLAGS.number_edges, metric=FLAGS.metric)
A = graph.adjacency(dist, idx)
# Connections are only vertical or horizontal on the grid.
# Corner vertices are connected to 2 neightbors only.
if corners:
import scipy.sparse
A = A.toarray()
A[A < A.max()/1.5] = 0
A = scipy.sparse.csr_matrix(A)
print('{} edges'.format(A.nnz))
print("{} > {} edges".format(A.nnz//2, FLAGS.number_edges*m**2//2))
return A
t_start = time.process_time()
A = grid_graph(28, corners=False)
A = graph.replace_random_edges(A, 0)
graphs, perm = coarsening.coarsen(A, levels=FLAGS.coarsening_levels, self_connections=False)
L = [graph.laplacian(A, normalized=True) for A in graphs]
print('Execution time: {:.2f}s'.format(time.process_time() - t_start))
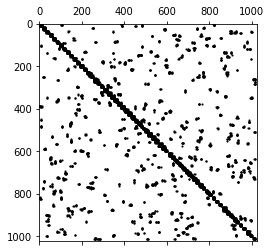
graph.plot_spectrum(L)
del A4.1:A = grid_graph(28, corners=False)
我们跳过前面的设计函数参数的部分,直接到创建网格图的部分
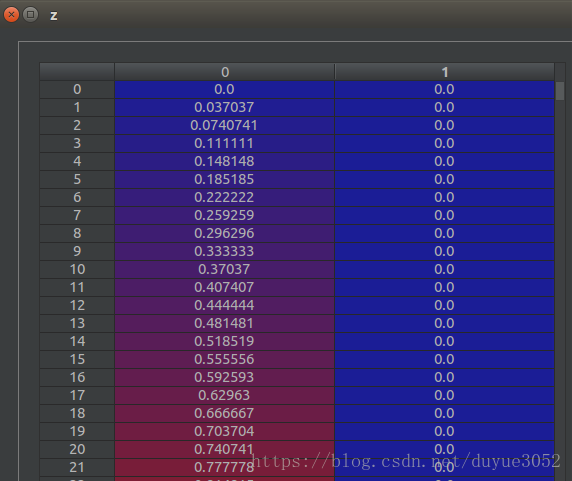
4.1.1:z = graph.grid(m)
生成一个28*28的网格图的每个点的坐标
4.1.2:graph.distance_sklearn_metrics graph.adjacency(dist, idx)
参见3.2,计算每个网格点28*28=784与其他网格点之间的距离。再选取每个点除本身外最近的8个点,形成邻接矩阵。
5:论文阅读
看了一个使用例子后,我们知道了运算的流程,但是对于为什么这么算,其背后的数学原理不清楚,接下来我们会阅读论文中的内容,然后看这种方法如何进行扩展
Laplacian变换
对图像不同维度的特征求一个邻接矩阵,矩阵中的值表示两个特征之间的权重。
谱图论
谱图理论就是研究如何通过几个容易计算的定量来描述图的性质。通常的方法是将图编码为一个矩阵然后计算矩阵的特征值(也就是谱 spectrum) 。
3.5节中讲述的卷积操作的前提就是把图像变换到傅里叶频率域,来做图的滤波操作。
Abstract
将CNN的计算能力,在不提高计算复杂度的情况下,从低维网格推广到高维无规则的图。前者可以推广到后者,反之不行。
For our graph model, we construct an 8-NN graph of the 2D grid which produces a graph of n = |V| = 976 nodes (28 2 = 784 pixels and 192 fake nodes as explained in Section 2.3) and |E| = 3198 edges. Following standard practice, the weights of a k-NN similarity graph (between features) are computed by
理论基础是——谱图论。
在MNIST和20NEWS上的实验展示了,这种以图结构为基础的网络,学习局部特征、静态特征、组合特征的能力。
Revisiting Classical CNNs on MNIST
CNN谱图滤波器的各向同性的性质决定了特征的方向旋转等的稳定。之前的方法采用的往往是数据增强。
邻接矩阵更好地组织了特征