《Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs》阅读笔记
文章概述
作者指出许多流行的GNN模型在泛化到异构图上时性能都很差,为此,作者确定了一组能够帮助提升GNN在异构图上性能的设计:
- 自嵌入和邻居嵌入分离
- 聚合更高阶的邻居
- 将中间层的表示组合作为最后的表示
作者将这些理念应用到了自己设计的 H 2 GCN \text{H}_{2}\text{GCN} H2GCN上,半监督结点分类任务(semi-supervised node classification task)的实验结果表明,这些idea能有效提升GNN在异构图上的性能,并且在同构图上也能取得不错的性能。
符号及概念介绍
为方便说明,首先给出论文中的符号表:
符号表中的 h h h和 H H H的介绍可以参加之前一篇博客《Graph Neural Network with Heterophily》阅读笔记(同一个作者的工作),其中:
- h h h表示图的同构等级,即图中相同类型结点间的边占图中所有边的比例,其值越大时表明图的同构性越强。
- H H H与 h h h不同,它包含了图中各种不同类型结点间包含边的比例。
此外,这里摘出 N ‾ i ( v ) \overline{N}_{i}(v) Ni(v)来进行介绍,它表示的是结点 v v v的 i − h o p i-hop i−hop( i i i阶邻居),例如下图中就给出了结点 v v v的 N ‾ 1 ( v ) \overline{N}_{1}(v) N1(v)和 N ‾ 2 ( v ) \overline{N}_{2}(v) N2(v)。
作者指出,如今许多GNN都遵从下列范式:
r v ( k ) = f ( r v ( k − 1 ) , { r u ( k − 1 ) : u ∈ N ( v ) } ) , r v ( 0 ) = x v , and y v = arg max { softmax ( r v ( K ) ) W } (1) \mathbf{r}_{v}^{(k)}=f\left(\mathbf{r}_{v}^{(k-1)},\left\{\mathbf{r}_{u}^{(k-1)}: u \in N(v)\right\}\right), \mathbf{r}_{v}^{(0)}=\mathbf{x}_{v}, \text { and } y_{v}=\arg \max \left\{\operatorname{softmax}\left(\mathbf{r}_{v}^{(K)}\right) \mathbf{W}\right\} \tag{1} rv(k)=f(rv(k−1),{ru(k−1):u∈N(v)}),rv(0)=xv, and yv=argmax{softmax(rv(K))W}(1)
即结点会不断聚合自身以及邻居的消息直至得到最终的结点表示 r v ( K ) r_v^{(K)} rv(K),然后经过softmax函数来获取结点属于各类别的概率。不同GNN的区别在于它们对于邻居和嵌入函数(embedding function)的定义。
异构图上的有效设计
自嵌入和邻居嵌入分离
在异构图中结点和其邻居的类别和特征表示可能是不同的,而许多GNN在聚合消息的时候往往直接将结点自身的消息和其邻居的消息混合在一起。例如GCN便是通过 A + I A + I A+I的操作使得结点自身和其邻居的消息通过共享权重矩阵聚合在了一起,但这种做法往往使得学习到的结点的特征表示与其邻居相似,这在异构图上是比较糟糕的。为此,作者提出将两者分离开来,即:
r v ( k ) = COMBINE ( r v ( k − 1 ) , AGGR ( { r u ( k − 1 ) : u ∈ N ˉ ( v ) } ) ) (2) \mathbf{r}_{v}^{(k)}=\operatorname{COMBINE}\left(\mathbf{r}_{v}^{(k-1)}, \operatorname{AGGR}\left(\left\{\mathbf{r}_{u}^{(k-1)}: u \in \bar{N}(v)\right\}\right)\right) \tag{2} rv(k)=COMBINE(rv(k−1),AGGR({ru(k−1):u∈Nˉ(v)}))(2)
在公式(2)中, N ‾ ( v ) \overline{N}(v) N(v)中不包含结点 v v v,聚合函数(AGGR)仅聚合结点 v v v的邻居的消息,然后将聚合得到的消息与结点 v v v自身的消息进行组合,最简单的方法是将二者拼接(Concatenation)起来。
聚合更高阶的邻居
为什么要聚合更高阶的邻居?作者先给出了两个概念:同构为主(homophily-dominant)和异构为主(heterophily-dominant)的领域。同构为主指结点的邻居与结点同类别的概率要比与结点不同类别的类别要大,反之则是异构为主。同构为主用公式表达为:
P ( y u = y v ∣ y v ) ≥ P ( y u = y ∣ y v ) , ∀ u ∈ N ( v ) a n d y ∈ Y ≠ y v (3) P\left(y_{u}=y_{v} \mid y_{v}\right) \geq P\left(y_{u}=y \mid y_{v}\right), \forall u \in N(v) \quad and \quad y \in \mathcal{Y} \neq y_{v} \tag{3} P(yu=yv∣yv)≥P(yu=y∣yv),∀u∈N(v)andy∈Y=yv(3)
我们知道在异构图中,结点的直接邻居往往是异构为主的,而更高阶的邻居可能是同构为主的,因此通过聚合更高阶的邻居可以提供更多相关的上下文信息。
将中间层的表示组合作为最后的表示
作者指出的第三个设计便是将结点的各层表示组合起来作为其最终的表示:
r v ( final ) = COMBINE ( r v ( 1 ) , r v ( 2 ) , … , r v ( K ) ) (4) \mathbf{r}_{v}^{(\text {final })}=\operatorname{COMBINE}\left(\mathbf{r}_{v}^{(1)}, \mathbf{r}_{v}^{(2)}, \ldots, \mathbf{r}_{v}^{(K)}\right) \tag{4} rv(final )=COMBINE(rv(1),rv(2),…,rv(K))(4)
其中组合函数可以为Concatentation、LSTM-attention等。在GNN中浅层(指GNN模型中头几层)会聚合更多的局部消息,而高层会聚合更多的全局信息,这种设计能够利用不同领域范围的消息从而能够学习到更具有表达能力的表示。
在理论上作者从谱视角(spectral perspective)给出了解释,将一个GCN风格层的传播过程看作光谱滤波,关于正则化邻接矩阵 A A A的高阶多项式可以看作一个低通滤波器,浅层的输出结果中包含更多的高频成分。对于异构图,其标签分布在高频中比低频包含更多的信息,因此通过组合中间各层的输出使得最后的表示中可以同时捕捉低频和高频成分。
H2GCN框架详解
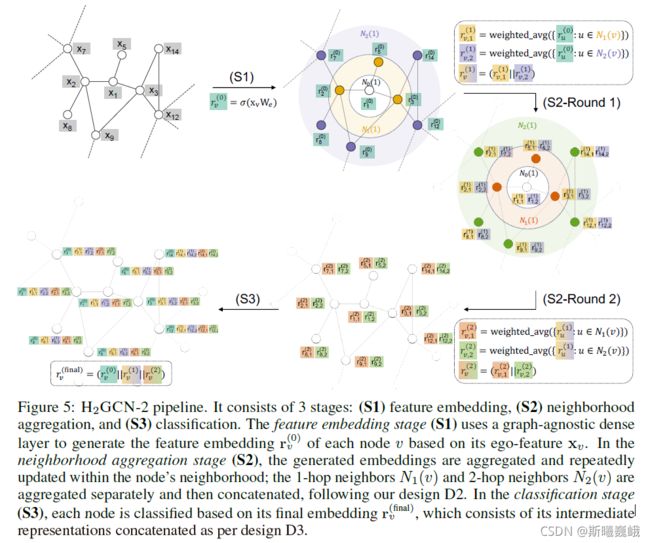
基于以上的三种idea,作者设计了H2GCN框架,下面是模型框架图:
H2GCN框架包含三个阶段:
- S1: 特征嵌入(feature embedding)
- S2: 邻居聚合(neighborhood aggregation)
- S3: 分类(classification)
特征嵌入阶段
第一阶段其实就是根据结点的特征来生成特征嵌入,即:
r v ( 0 ) = σ ( x v W e ) (5) \mathbf{r}_{v}^{(0)}=\sigma\left(\mathbf{x}_{v} \mathbf{W}_{e}\right) \tag{5} rv(0)=σ(xvWe)(5)
其中 x v \mathbf{x}_{v} xv为结点 v v v自身的特征, W e W_{e} We为可学习的权重矩阵, σ \sigma σ为非线性函数。
第一阶段相当于结点特征过一个单层无偏差(bias)的MLP来生成自身的特征嵌入。
邻居聚合阶段
第二阶段为 K K K轮的一阶邻居和二阶邻居聚合,每轮阶段都会聚合自身的 1 − h o p 1-hop 1−hop和 2 − h o p 2-hop 2−hop邻居消息:
r v ( k ) = COMBINE ( AGGR { r u ( k − 1 ) : u ∈ N ˉ 1 ( v ) } , AGGR { r u ( k − 1 ) : u ∈ N ˉ 2 ( v ) } ) (6) \mathbf{r}_{v}^{(k)}=\operatorname{COMBINE}\left(\operatorname{AGGR}\left\{\mathbf{r}_{u}^{(k-1)}: u \in \bar{N}_{1}(v)\right\}, \operatorname{AGGR}\left\{\mathbf{r}_{u}^{(k-1)}: u \in \bar{N}_{2}(v)\right\}\right) \tag{6} rv(k)=COMBINE(AGGR{ru(k−1):u∈Nˉ1(v)},AGGR{ru(k−1):u∈Nˉ2(v)})(6)
作者使用的 COMBINE \text{COMBINE} COMBINE函数为concatenation:
r v ( k ) = ( r v , 1 ( k ) ∥ r v , 2 ( k ) ) (7) \mathbf{r}_{v}^{(k)}=\left(\mathbf{r}_{v, 1}^{(k)} \| \mathbf{r}_{v, 2}^{(k)}\right) \tag{7} rv(k)=(rv,1(k)∥rv,2(k))(7)
AGGR \text{AGGR} AGGR为度归一化(degree-normalized average)平均:
r v , i ( k ) = AGGR { r u ( k − 1 ) : u ∈ N ˉ i ( v ) } = ∑ u ∈ N ˉ i ( v ) r u ( k − 1 ) d v , i − 1 / 2 d u , i − 1 / 2 (8) \mathbf{r}_{v, i}^{(k)}=\operatorname{AGGR}\left\{\mathbf{r}_{u}^{(k-1)}: u \in \bar{N}_{i}(v)\right\}=\sum_{u \in \bar{N}_{i}(v)} \mathbf{r}_{u}^{(k-1)} d_{v, i}^{-1 / 2} d_{u, i}^{-1 / 2} \tag{8} rv,i(k)=AGGR{ru(k−1):u∈Nˉi(v)}=u∈Nˉi(v)∑ru(k−1)dv,i−1/2du,i−1/2(8)
其中 r v , i ( k ) r_{v,i}^{(k)} rv,i(k)表示对结点 v v v的第 i i i阶邻居进行度归一化平均, d v , i = ∣ N ‾ i ( v ) ∣ d_{v,i}=|\overline{N}_{i}(v)| dv,i=∣Ni(v)∣表示结点 v v v的 i − h o p i-hop i−hop邻居的数量。
阶段2作者并没有在聚合邻居消息的时候同时聚合自身的,此外作者去掉了非线性函数 σ \sigma σ。
分类阶段
分类阶段作者把每层的中间表示进行拼接(concatenation):
r v ( final ) = COMBINE ( r v ( 0 ) , r v ( 1 ) , … , r v ( K ) ) (9) \mathbf{r}_{v}^{(\text {final })}=\operatorname{COMBINE}\left(\mathbf{r}_{v}^{(0)}, \mathbf{r}_{v}^{(1)}, \ldots, \mathbf{r}_{v}^{(K)}\right) \tag {9} rv(final )=COMBINE(rv(0),rv(1),…,rv(K))(9)
然后过softmax层来对结点的标签进行预测:
y v = arg max { softmax ( r v ( final ) W c ) } (10) y_{v}=\arg \max \left\{\operatorname{softmax}\left(\mathbf{r}_{v}^{(\text {final })} \mathbf{W}_{c}\right)\right\} \tag{10} yv=argmax{softmax(rv(final )Wc)}(10)
实验
数据集
作者生成具有几种不同 h h h值的图来进行实验:
实验过程中数据集对应训练集、验证集和测试集的划分比例分别为每个类25%、25%、50%。作者使用的评价指标为基准数据集生成的对应于每个 h h h值的三个图上的平均准确率和标准差。
同构等级从0, 0.1, 0.2, …, 1共11个,每个同构等级对应三个生成的图,每个同构等级生成3个图。
实验结果与分析
从下图的实验结果可以看出H2GCN-2在异构性强( h h h值小)的图上比其它模型表现的都要好,同时在同构性强( h h h值大)的图上也能取得与其它模型相当的性能。
H2GCN-2最后的2是 K K K的值。
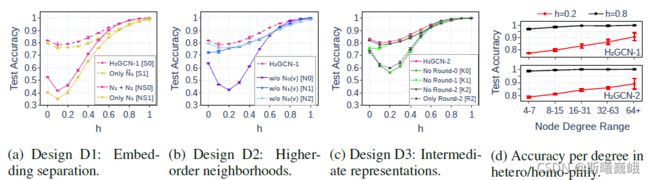
作者还设计了消融实验来验证三个设计的有效性,具体结果参加下图。
对于自嵌入和邻居嵌入分离的有效性验证,作者设置了4个对照组:
- S 0 S_0 S0:同时聚合 N ‾ 1 \overline{N}_1 N1和 N ‾ 2 \overline{N}_2 N2邻居消息;
- S 1 S_1 S1:仅聚合 N ‾ 1 \overline{N}_{1} N1邻居消息;
- N S 0 NS_{0} NS0:同时聚合 N 1 N_{1} N1和 N 2 {N_{2}} N2邻居消息;
- N S 1 NS_{1} NS1:仅聚合 N 1 N_{1} N1邻居消息;
从(a)的结果可以看出,将自嵌入和邻居嵌入分来在图强异构性的情况下都要好于对应的未分开的。
对于聚合更高阶邻居的有效性验证,作者设置了额外的3个对照组:
- N 0 N_{0} N0:没有聚合0阶邻居(每个自嵌入);
- N 1 N_{1} N1:没有聚合 N ‾ 1 \overline{N}_{1} N1邻居消息;
- N 2 N_{2} N2:没有聚合 N ‾ 2 \overline{N}_{2} N2邻居消息;
从(b)的结果可以看出H2GCN-1的性能最佳,这说明组合各阶邻居的效果最好。同时从结果可以看出去掉0阶邻居的性能下降最厉害,其次是 N 1 N_{1} N1、 N 2 N_{2} N2,这表明结点自身的特征在异构设置下非常重要,而高阶邻居则在同构设置贡献大。而设计2可以让我们组合不同邻域的信息,使得模型能够适用于各种同构率的图。
对于组合各中间层表示的有效性验证,作者也设置了4个对照组:
- K 0 K_{0} K0:去掉第0层的中间表示;
- K 1 K_{1} K1:去掉第1层的中间表示;
- K 2 K_{2} K2:去掉第2层的中间表示;
- R 2 R_{2} R2:仅使用最后一层的表示来作为结点最后的嵌入;
从(c )的结果可以看出同时使用各层的效果是最佳的,这表明该设计是有效的。此外作者还对结点的度进行了消融,从实验结果(d)可以看出在强异构的图时,度低时要比度高时的性能差一截,而强同构度低度和高度的性能差别却不是很大。