数据结构学习心得——树
数据学习结构心得——树
我觉得树这部分挺难,但是挺有意思的,内容比较多,为了考试整理一波,里面有很多我自己的思考和看法,有的方法并不一定好理解而且有很多瑕疵,希望大家可以多包含,有些图片偷了老师的ppt,我觉得老师应该不会介意吧哈哈哈哈。内容主要分为以下几块:
1.树及其特点、性质及基本概念,森林
2.二叉树定义、性质及其相关知识点
3.哈夫曼树
树及其特点、性质及基本概念,森林
树的定义:树是由 n (n ≥ 0) 个结点组成的有限集合。如果 n = 0,称为空树;如果 n > 0,则有一个特定的称之为根(root)的结点,它只有直接后继,但没有直接前驱;除根以外的其他结点划分为 m (m ≥ 0) 个 互不相交的有限集合T0, T1, …, Tm-1,每个集合又是一棵树,并且称之为根的子树。
树的特点:每棵子树的根结点有且仅有一个直接前驱,但可以有0个或多个直接后继。
树的一些基本概念:
结点:存储数据元素和指向子树的链接,由数据元素和构造数据元素之间关系的引用组成。
孩子结点:树中一个结点的子树的根结点称为这个结点的孩子结点。
双亲结点:树中某个结点有孩子结点(即该结点的度不为0),该结点称为它孩子结点的双亲结点,也叫前驱结点。
兄弟结点:具有相同双亲结点(即同一个前驱)的结点称为兄弟结点。
结点的度:结点所有子树的个数称为该结点的度。
树的度:树中所有结点的度的最大值称为树的度。
叶子结点:度为0的结点称为叶子结点,也叫终端结点。
分支结点:度不为0的结点称为分支结点,也叫非终端结点。
结点的层次:从根结点到树中某结点所经路径的分支数称为该结点的层次。根结点的层次一般为1(也可以自己定义为0),这样,其它结点的层次是其双亲结点的层次加1.
树的深度:树中所有结点的层次的最大值称为该树的深度(也就是最下面那个结点的层次)。
有序树和无序树:树中任意一个结点的各子树按从左到右是有序的,称为有序树,否则称为无序树。
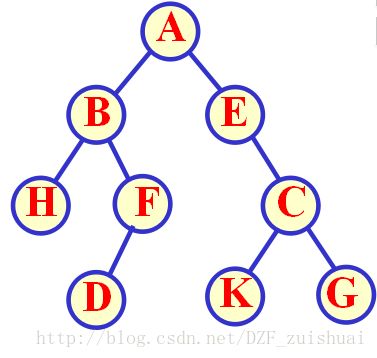
如图,该树的深度为4(设根节点为1),树的度为3,节点A度也为3。

森林的定义
N(N >= 0)棵互不相交的树称为森林。
二叉树定义、性质及其相关知识点
二叉树的定义:一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。
满二叉树的定义:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
完全二叉树的定义:若设二叉树的高度为h,则共有h+1层。除第 h 层外,其它各层 (0 ~h-1) 的结点数都达到最大个数,第 h 层从右向左连续缺若干结点,这就是完全二叉树。(这里加粗的文字隐含了n-1层二叉树节点只允许出现右孩子缺省或左右都缺的含义)
完美二叉树定义:满足完全二叉树性质,树的叶子节点均在最后一层。
理想平衡二叉树:任意两个叶节点的深度之差不超过1,即任意节点左右子树深度之差绝对值不超过1。
二叉树的性质:
1)若二叉树的层次从0开始, 则在二叉树的第 i 层最多有 2^i 个结点。(i >= 0)。
2)高度为 h 的二叉树最多有 2^(h+1)-1个结点。(h >= -1)
3)对任何一棵二叉树, 如果其叶结点有 n0 个, 度为2的非叶结点有 n2 个, 则有n0=n2+1。
4)具有 n (n >= 0) 个结点的完全二叉树的高度为log2(n+1) -1.
5)如将一棵有n个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号0, 1, 2, …, n-1,则有以下关系:
若i = 0, 则 i 无双亲
若i > 0, 则 i 的双亲为(i -1)/2
若2*i+1 < n, 则 i 的左子女为 2*i+1
若2*i+2 < n, 则 i 的右子女为2*i+2
若 i 为偶数, 且i != 0, 则其左兄弟为i-1
若i 为奇数, 且i != n-1,则其右兄弟为i+1
二叉树的顺序存储
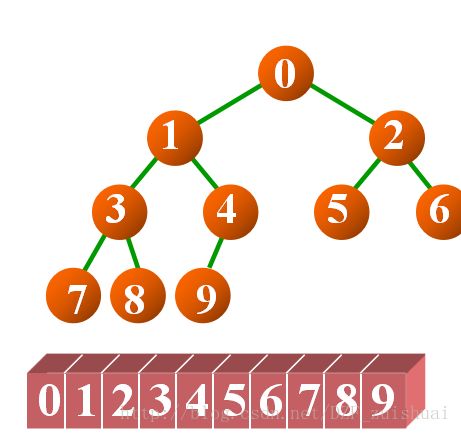
对于一个二叉树的存储,首先想到的是能不能用一个数组顺序表存储,用数组下标映射每个节点的存储位置。事实是是可行的,但是存在着诸多问题。
对于完全二叉树是完全可行的,但是对于一般二叉树,就会出现空间浪费的问题。
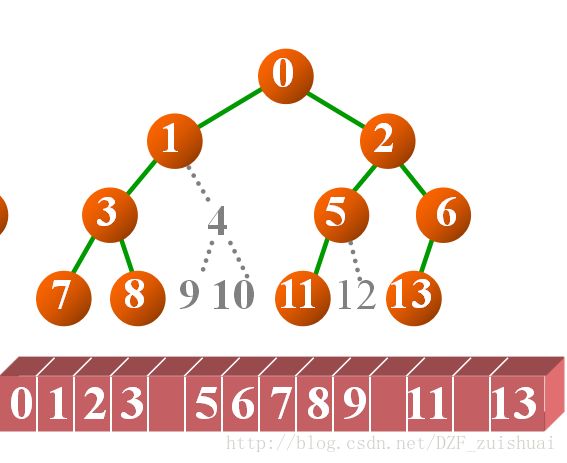
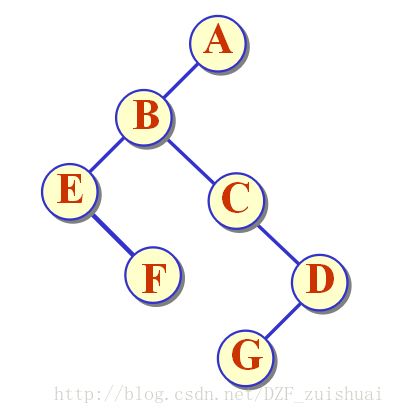
如图,左侧是完全二叉树,右图是一般二叉树,这个时候会发现,对于非完全二叉树,数组空间明显出现了浪费。这就体现出了完全二叉树的优越性,也体现了使用顺序表存储的缺点所在。
二叉树的链式存储
于是,一个高端的方法出现了——链式存储,使用二叉链表存储二叉树,是一个很棒的选择。如下图一样,十分直观,而且方便。
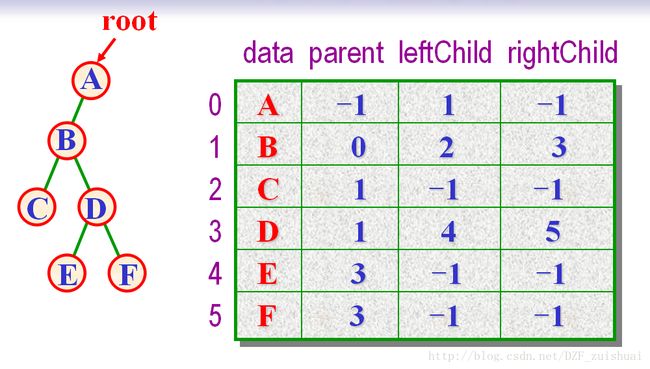
对于二叉链表,还可以用静态方式表示,如下图
从左到右,从上到下,编号0,1,2,3,4,5,按上图表格填入双亲、左右孩子,没有父母或孩子用-1表示,就ok了。
二叉树的遍历(必考)
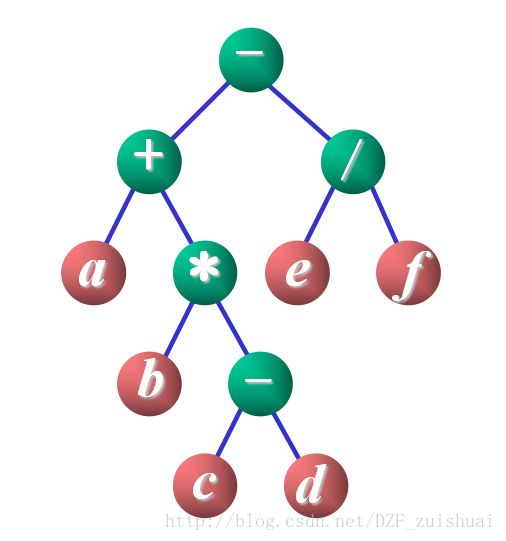
树的遍历就是按某种次序访问树中的结点,要求每个结点访问一次且仅访问一次。先上图,不多bb。
1)前序遍历:
说白了就是先根后左再右。因为树的遍历是一个递归的定义,所以在前序遍历的时候就是先把根给读了,然后再读左边,遇到节点就读根,然后读右边,就这样解决了。
按上图看,前序结果就是:-+a*b-cd/ef
2)中序遍历:
就是先读左再读根再读右。遇到节点就一右到底,右到头了没法右了,就读根,然后读左,再一左到底,重复上面的操作,就OK了。
按照上图,中序遍历的结果就是:a+b*c-d-e/f
3)后序遍历:
和上面基本操作一样,只不过是先左再右最后根,不多说,直接说结果:abcd-*+ef/-
根据遍历结果画二叉树(必考)
出这种题的理论依据,就是由二叉树的前或后序序列和中序序列可唯一地确定一棵二叉树。也就是说,只要有中序,其他两个二选一,都可以确定唯一一棵二叉树。
直接上题:已知前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG },请画出该二叉树。
方法并不复杂,前序确定了A,那么可以看中序A所在的位置,然后找出两个A的子树,对子树进行上述同样的操作,就画出来了。
树和森林转化二叉树(必考)
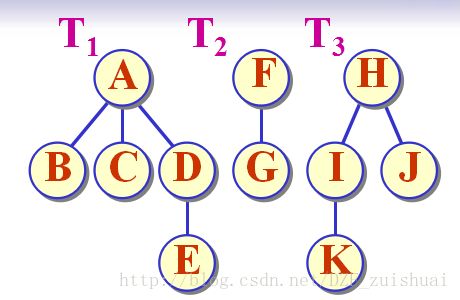
只需要急一句话:左子女,右兄弟。也就是说,把树或者森林转化成二叉树,只需要把二叉树的左边指针指向孩子,右边指针指向兄弟即可。直接上图就能看懂了:
就是这么简单,森林也是一样的,只不过把几棵树当成了兄弟而以:
除了把森林和树转化成二叉树,还需要知道怎么把二叉树转化回去,这个比起上面的更简单,在此不再累述。
树和森林的遍历
树的遍历方法和二叉树差不多,但是建议先把二叉树还原成树再进行遍历,因为存在着一些问题,导致二叉树的遍历结果可能和树的遍历结果不同。
树的遍历分两大类:层次遍历与深度遍历。
先看层次遍历,就是按树的层次,从上到下、从左到右依次遍历,按上面的图来看,树的层次遍历结果是ABCDEFG,而它的二叉树表示情况下,层次遍历就成了ABECFDG,显然不一样,所以建议先还原再遍历。其实想想也是可以直接用二叉树去写遍历结果的,想一下,左子女右兄弟,从根开始读了左之后,先右后左读出来就好了。
再看深度遍历,先根序和后根序,记住两句话,1.树的后根遍历结果与其对应二叉树表示的中序遍历结果相同。2.树的先根遍历结果与其对应二叉树表示的前序遍历结果相同。就是这么简单就解决了,至于原因,稍微想一想,试一试就知道了。
至于森林,和上文说到的树的遍历方法大致是一样的,实在记不住,就把它恢复原状就ok啦。
哈夫曼树
什么是哈夫曼树?
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。那么问题来了,什么是路径,什么是带权路径呢?那么下面给出几个基本概念。
路径:树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度:路径上的分枝数目称作路径长度。
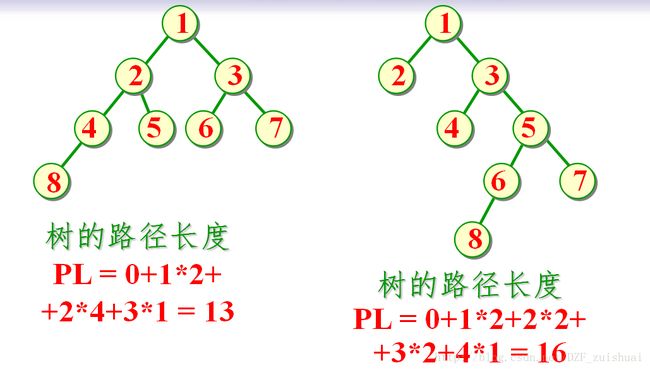
树的路径长度PL:从树根到每一个结点的路径长度之和。
结点的带权路径长度:在一棵树中,如果其结点上附带有一个权值,通常把该结点的路径长度与该结点上的权值之积成为带权路径。
树的带权路径长度WPL:如果树中每个叶子上都带有一个权值,则把树中所有叶子的带权路径长度之和称为树的带权路径长度。

WPL = 13*1+7*2+2*3+5*3
(图偷的老师的,老师应该不会介意对吧)
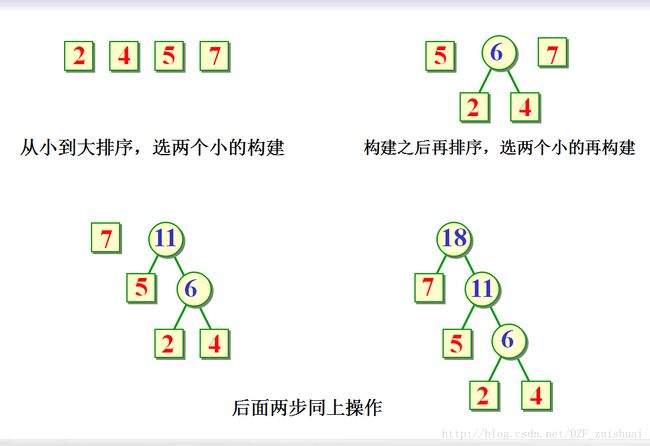
怎么构造哈夫曼树?
为了方便构造,我对哈夫曼算法的原始表述进行了一些修改,为了便于理解,拿一个题为例解释,其实就是排序、构造、排序、构造而以。
百度经验好像有这个方法的介绍,附上一波链接:https://jingyan.baidu.com/article/a501d80c16dfa0ec620f5e70.html