浅谈差分约束系统

1.从代数到图论

1.1.差分约束方程

差分约束方程就是形如 \(x_i-x_j \leq w_{ij}\) 或 \(x_i-x_j \geq w_{ij}\) 的方程组

比如说：

\(\begin{cases}x_1-x_3 \leq 5 \\x_1-x_2 \leq 2 \\x_2-x_1 \leq 0 \\x_2-x_3 \leq 2 \\x_3-x_2 \leq -1 \\ x_3-x_1 \leq -2 \end{cases}\)

就是一组差分方程。
下面是它的一组解：

\(\begin{cases}x_1=5 \\x_2=3 \\x_3=1 \end{cases}\)

一组差分约束方程要么有无穷组解，要么无解。因为如果它有解，那么它的解同时加上一个实数 \(k\)，依旧是一组解。因为每个数都加\(k\)，他们任意两个数之间的差是不变的，所以对于不等式没有影响。

---

\(\mathtt{For}\ \mathtt{Example}:\)

上式的解还可以是
\(\begin{cases}x_1=6 \\x_2=4 \\x_3=2 \end{cases}\)
（同时加\(1\)）

---

1.2.图论解法

多数博客接下来是这么说的：

看到 \(x_i - x_j \leq w_{ij}\)
有没有想到什么呢？ 可以变形为 \(x_i \leq x_j + w_{ij}\) ,这与单元最短路中的三角形不等式\(D_i<=D_j+w_{ij}\)非常相似

因此，可以把每个变量 \(x_i\) 看做有向图中的一个结点\(i\),对于约束条件 \(X_i - X_j ≤ w_{ij}\) ,从结点\(j\)向结点i连一条权值为 \(w_{ij}\) 的有向边。

这里补充一下：\(D_i\)就是上面\(x_i\)的一组解。

讲得是没错，然而，凭什么长得像就可以随便乱套呢？

首先第一步最开始，
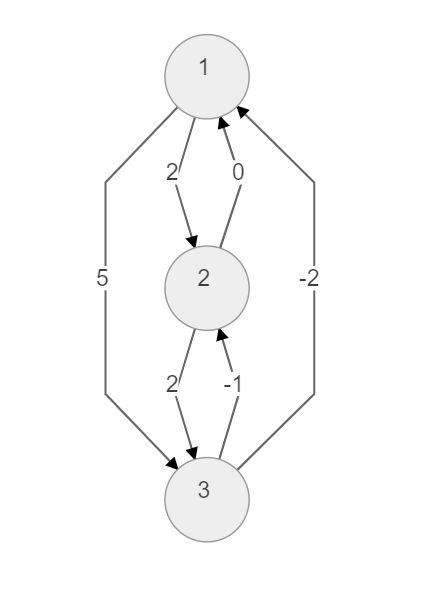
我们画张图看看：

比如对于\(x_1-x_3 \leq 5\)，如果有当前从1到3的最短路大于5，那么一定会被这条路（\(1\rightarrow3\)）替换掉。

同理，对于 \(x_i-x_j \leq w_{ij}\)，如果有当前从\(i\)到\(j\)的最短路大于\(w_{ij}\)，那么一定会被这条路（\(i\rightarrow j\)）替换掉。

大于也是同样的原理，可以举一反三。

同理可得其它边，以保证在前提（差分约束方程）不被违反的情况下得到最优解。

2.差分约束系统

2.1.大于还是小于

众所周知，不等式方程是互通的，它们可以互相转换。

---

\(\mathtt{For}\ \mathtt{Example}:\)

刚才的方程组：

\(\begin{cases}x_1-x_3 \leq 5 \\x_1-x_2 \leq 2 \\x_2-x_1 \leq 0 \\x_2-x_3 \leq 2 \\x_3-x_2 \leq -1 \\ x_3-x_1 \leq -2 \end{cases}\)

等价于：

\(\begin{cases}x_3-x_1 \geq -5 \\x_2-x_1 \geq -2 \\x_1-x_2 \geq 0 \\x_3-x_2 \geq -2 \\x_2-x_3 \geq 1 \\ x_1-x_3 \geq 2 \end{cases}\)

---

那么差分约束系统该用大于还是小于呢？

事实上，两者都有使用，具体看情况。

小于求最短路得到最大值，

大于求最长路得到最小值。

2.2.无解情况

并不是所有差分约束方程都有解。大致可分为两类：

2.2.1.条件矛盾

顾名思义，满足了条件A就无法满足条件B。

---

\(\mathtt{For}\ \mathtt{Example}:\)

\(\begin{cases}x_1-x_2 \leq 5 \\ x_2-x_1 \leq -6\end{cases}\)

等价于：

\(\begin{cases}x_1-x_2\leq5 \\ x_1-x_2\geq6\end{cases}\)

---

2.2.2.无关未知数

这个其实不一定算无解，不过和2.2.1判断方法一致，就勉强算无解吧。
未知数没有构成强连通分量。

---

\(\mathtt{For}\ \mathtt{Example}:\)

\(\begin{cases}x_1-x_2 \leq 5 \\ x_3-x_1 \leq 2\\ x_4-x_5 \leq 2 \\ x_5-x_6 \leq -3\end{cases}\)

这里
\(x_1,x_2,x_3\)与\(x_4,x_5,x_6\)毫无关联。

---

2.2.3.判断无解

最短路有负环或最长路有正环即为无解。

2.3.超级原点

超级原点连接到所有点，且权值都是0。

在求最长路时，可以加入一个超级原点以简化代码。

最短路似乎好像也许可能可以加入超级原点，不过容易引起错误。

2.4.去除重边

重复的边会容易导致错误（误判负环）
去重边的伪代码

flag <- 1
for i in G[u]
    if G[u,i].v = v
        if w better than G[u,i].w
            set new G[u,i].w
        flag <- 0;

if flag = 1
    G[u].append(v, w)

3.模板代码

就是一个spfa模板：

bool spfa() {
    memset(d, 0xef, sizeof(d));
    d[0] = 0;
    q.push(0);
    tx[0] = 1;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        vis[u] = 0;
        for(unsigned i = 0; i < G[u].size(); ++i) {
            int v = G[u][i].v;
            int dis = G[u][i].w;
            if (d[v] > d[u] + dis) {
                d[v] = d[u] + dis;
                if (++tx[v] >= 40) {
                    return 0;
                }
                if (!vis[v]) {
                    q.push(v);
                    vis[v] = 1;
                }
            }
        }
    }
    return 1;
}

最长时改一下符号：

if (dis[v] < dis[u] + w) {
    --snip--
}

4.例题

P1993 小K的农场

模板题，长短路均可，主要问题是如何插入边：

scanf("%d %d", &n, &m);
for (int i = 1; i <= m; ++i) {
    scanf("%d %d %d", &t, &a, &b);
    if (t == 3) {
        G[a].push_back(node(b, 0));
        G[b].push_back(node(a, 0));
    } else {
        scanf("%d", &c);
        if (t == 1) {
            G[a].push_back(node(b, c));
        } else {
            G[b].push_back(node(a, -c));
        }
    }
}

tyvj-p1277 关系运算图

好像现在看不到题了：

Description

给出一有向图，图中每条边都被标上了关系运算符‘<’,‘>’,‘=’。现在要给图中每个顶点标上一个大于等于0,小于等于k的某个整数使所有边上的符号得到满足。若存在这样的k，则求最小的k，若任何k都无法满足则输出NO。

例如下表中最小的k为2。

结点1>结点2

结点2>结点3

结点2>结点4

结点3=结点4

如果存在这样的k，输出最小的k值；否则输出‘NO’。

Input

共二行，第一行有二个空格隔开的整数n和m。n表示G的结点个数，m表示G的边数，其中1<=n<=1000, 0<=m<=10000。全部结点用1到n标出，图中任何二点之间最多只有一条边，且不存在自环。

第二行共有3m个用空格隔开的整数，第3i-2和第3i-1（1<=i<=m）个数表示第i条边的顶点。第3i个数表示第i条边上的符号，其值用集合{-1，0，1}中的数表示：-1表示‘<’, 0 表示‘=’, 1表示‘>’。

Output

仅一行，如无解则输出‘NO’；否则输出最小的k的值。

Sample Input

4 4

1 2 -1 2 3 0 2 4 -1 3 4 -1

Sample Output

2

模板题，最长路

HDU3440 House Man

最短路，如果最高楼在最矮楼左边就翻转高度数组。

@2019-7-31 贵州铜仁镇远古镇