连乘次数
是一个矩阵,是一个矩阵,相乘,得到的矩阵元素个数为,每个元素由次乘法得到,因此所需乘法次数为。
问题描述
在计算矩阵连乘积时,加括号的方式对计算量有影响。
例如有三个矩阵连乘,它们的维数分别为
,,。用第一种加括号方式计算,则所需数乘次数为。用第二种加括号方式计算,需要次数乘。
输入连乘矩阵的个数,每个矩阵的维数。要求输出数乘次数最少时的加括号方式,及数乘次数。
Sample Input
6
30 35
35 15
15 5
5 10
10 20
20 25
Sample Output
15125
((A1(A2A3))((A4A5)A6))
解题思路:
先引入以下符号:
- 表示矩阵的个数
- 表示第个矩阵
- 表示矩阵连乘
- 表示的列数
- 表示的行数
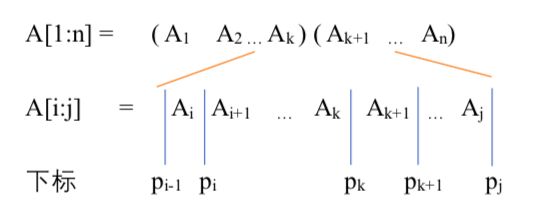
- 表示矩阵连乘断开的位置为,表示在和之间断开
- 表示的最少乘次,即问题的最优解
符号解释:由矩阵相乘的条件可知:前一个矩阵的列数 = 后一个矩阵的行数。因此,既是的列数,也是的行数。结合下面的示意图有助于理解:
该问题有一个关键特征:计算矩阵链的最优计算方式,包含了子矩阵链和的最优计算方式。
一般地,如果原问题的最优解,包含了其子问题的最优解,则我们称这种性质为最优子结构性质。若问题具有最优子结构性质,则可用动态规划算法求解。
首先,建立递归关系,写出递归公式:
公式解释:假设是对矩阵链一分为二得到最优解时的断开位置,则和分别是两个子矩阵链和的最优解。两个矩阵最后要相乘才能得到,因此,最后要加上,也就是两子矩阵相乘的数乘次数,才能得到总的数乘次数。
然后,根据递归公式计算最优解。
在程序中,m的实现是一个二维数组,也就是一张二维表,为了方便计算,m的下标从1开始。要计算的最少乘次,本质上是求m[1][n]的值,也就是二维表表右上角的值.
例如,连乘矩阵个数为6,维数分别为:
,
,
,
,
,
填表方式如下图所示:
原问题现已转化为填表问题,要填充的是矩阵右上三角部分的值。
根据递归公式,对角线的值为0。其他值需要根据于断开位置的值来得到,,我们要遍历所有,就要访问所求值的所有同一行左边的值和同一列下方的值。因此,在代码中我们可以使用自底向上、从左到右的计算顺序来依次填充,最终得到右上角的值。
例如:
伪代码如下:
for (int i = n; i >= 1; i--) //i表示行
{
for (int j = i; j <= n; j++) //j表示列
{
if (i == j)
m[i][j] = 0;
else
m[i][j] = CalculateMin(i,j);
}
}
完整代码
//矩阵连乘问题,递归方程采用课本P47的递归方程。
//与课本P47的程序相比,两者都是填m[][]的上三角,
//但本程序是横向填表,而课本程序是斜向填表。
//本程序按照 自底向上,自左向右 的顺序来计算m[][]的上三角。
//程序中有记录相应断开位置到s[][]。
#include
using namespace std;
void MatrixChain(int, int[], int **, int **);
void print(int, int, int **);
void CalculateMin(int i, int j, int p[], int **m, int **s);
int main()
{
int n;
cin >> n;
int *tempP = new int[2 * n]; //p[0]为A1的行数;p[i]为Ai的列数
int *p = new int[n + 1]; //p[0]为A1的行数;p[i]为Ai的列数
int **m = new int *[n + 1]; //m[i][j]为Ai连乘到Aj的最少乘次数
int **s = new int *[n + 1]; //s[i][j]为 Ai连乘到Aj的最优解的第一层断开位置
for (int i = 1; i <= n; i++)
{
m[i] = new int[n + 1];
s[i] = new int[n + 1];
}
for (int i = 0; i < 2 * n; i++)
{
cin >> tempP[i];
}
for (int i = 0; i <= n; i++)
{
p[i] = i == 0 ? tempP[0] : tempP[i * 2 - 1];
}
MatrixChain(n, p, m, s);
cout << m[1][n] << endl; //最优值存储在m[1][n]
//print(1, n, s); //打印最优计算方式
return 0;
}
void MatrixChain(int n, int p[], int **m, int **s)
{
//以下双重循环对m[][]的上三角进行填表
//填表顺序为自底向上,自左向右
for (int i = n; i >= 1; i--) //i表示行
{
for (int j = i; j <= n; j++) //j表示列,因为只填上三角,所以j的初值为i
{
//以下按照矩阵连乘问题的递归公式来求每一个m[i][j]
if (i == j)
{
m[i][j] = 0;
}
else
{
CalculateMin(i, j, p, m, s);
}
}
}
}
void CalculateMin(int i, int j, int p[], int **m, int **s)
{
m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j]; //若i与j不相等,m[i][j]的初值为断开位置为i时的最优值
s[i][j] = i; //记录当前断开位置位置为i
for (int k = i + 1; k < j; k++) //k用于尝试不同的断开位置
{
int curr = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (curr < m[i][j]) //当前k值作为Ai连乘到Aj的断开位置能获得更少计算量
{
m[i][j] = curr; //刷新最优值
s[i][j] = k; //刷新相应断开位置
}
}
}
void print(int i, int j, int **s)
{
if (i == j)
cout << "A" << i;
else
{
cout << "(";
print(i, s[i][j], s);
print(s[i][j] + 1, j, s);
cout << ")";
}
}
可以在这个网站上检验一下程序的正确性:https://onlinejudge.u-aizu.ac.jp/problems/ALDS1_10_B
参考资料:《计算机算法设计与分析》(第四版)p44-p49