我也不知道为啥突然跑来写这个东西……
可能最近考太频繁??权当攒RP了。
说的好像真的有人会看一样。
0/0:引言
主席树,全名可持久化线段树,由一位名叫黄嘉泰(hjt)的大神在考场上yy出来。
所谓可持久化线段树,就是可以查询历史更新信息的线段树。
假如我有一棵线段树,维护一个长度为n的序列,称为历史版本1。
随后我对它进行m次操作,使其发生变化称为历史版本2、历史版本3……历史版本n。
此时我要查询历史版本3中的某一个区间的信息,该怎么办?
重新建树?$n,m \leq 1e5$。啊啊啊啊啊啊啊啊啊啊……
咦,那闪耀着救世主光辉的数据结构是……
当然是:主席树!
前置技能点:
- 动态开点线段树(不仅省空间,还可以进化成为主席树!)
- 前缀和思想(普遍的优化手段,静态区间查询的平民神器!)
0/1:思想
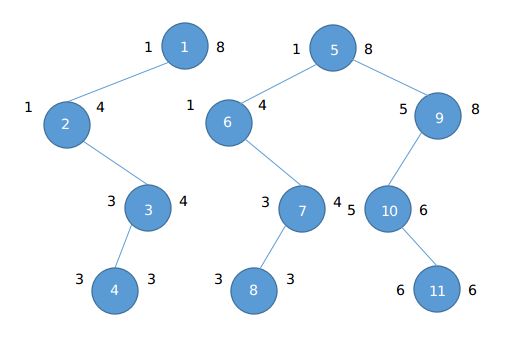
对于上面引言中提到的问题,我们考虑一个建树的过程。(以下仅考虑值域为8的情况)
最暴力的思想是,拿到一棵空线段树,我们分别建立它的历史版本以供最终查询。
建树过程如下:
1.在历史版本1中插入一个元素$3$
2.新建一棵树称为历史版本2,复制之前的树并插入一个元素$6$。
点数爆增有没有。
然后我们就发现,每插入一个单点的时候,整棵树的信息并非全部发生了变化。
那么新建一棵树就会放弃对这些信息的利用,浪费了空间。
主席树的实现正是基于利用这些信息来达成节省空间的目的。
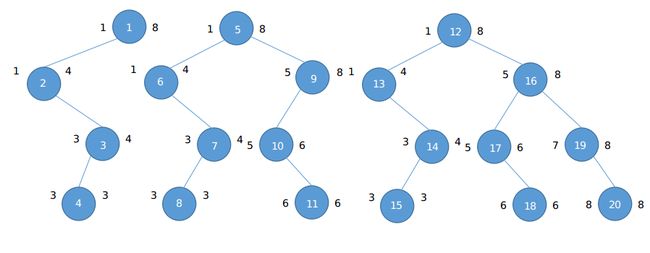
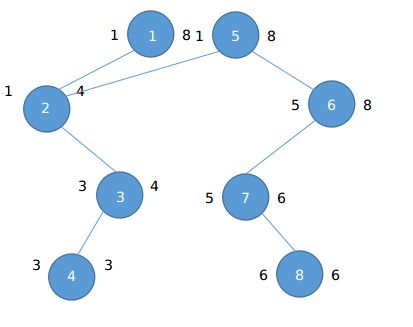
下面是对于上面的问题的主席树建树方法:
1.新建一棵线段树并插入一个元素$3$,建树操作同暴力建树第一步。
2.插入一个元素$6$。
每建立一棵树都会利用历史版本中没有被改变的那一部分
空间复杂度明显下降是了吧。
0/2:代码实现(这里是一些基本操作$OvO$)
我自己手里好像还真没有啥能拿出手的板子……
建树操作:(在某历史版本的主席树上插入一个权值为$val$的元素)
传参:当前节点k、当前节点维护的值域区间左右端点、要继承的历史版本节点his、插入的值val
首先要新建节点。递归到当前层说明这一层一定被改变了。所以直接新建无需判定。
将左儿子和右儿子都先附成历史版本节点的左右儿子节点。有更改会在下一层递归新建并更改。
然后改变当前节点信息。随后继续递归向下插入即可。
inline void insert(int &k,int l,int r,int his,int val) { k=++type; ls[k]=ls[his]; rs[k]=rs[his]; sum[k]=sum[his]+1; if(l==r)return ; int mid=l+r>>1; if(val<=mid)insert(ls[k],l,mid,ls[his],val); else insert(rs[k],mid+1,r,rs[his],val); }
查询操作:(查询第k小值)
传参:查询区间左右端点的主席树当前节点编号、当前维护的值域区间左右端点、查询的权值
将查询的权值与当前搜索到的值域中点相比较,
若$val \leq mid$则向左继续查询第$val$小的值,
否则向右查询第$val-cnt$小的值。($cnt$为主席树当前节点右儿子的大小)
int query(int k1,int k2,int l,int r,int val) { if(l==r)return l; int mid=l+r>>1; int cnt=sum[ls[k2]]-sum[ls[k1]]; if(val<=cnt)return query(ls[k1],ls[k2],l,mid,val); else return query(rs[k1],rs[k2],mid+1,r,val-cnt); }
#include#include #include using namespace std; const int N=100005; int type,n,m,side; int sum[N*20],root[N*20],ls[N*20],rs[N*20]; int a[N],b[N]; inline int read() { int f=1,x=0;char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();} return x*f; } void build(int &k,int l,int r) { k=++type; sum[k]=0; if(l==r)return ; int mid=l+r>>1; build(ls[k],l,mid); build(rs[k],mid+1,r); } void update(int &k,int l,int r,int time,int val) { k=++type; ls[k]=ls[time]; rs[k]=rs[time]; sum[k]=sum[time]+1; if(l==r)return ; int mid=l+r>>1; if(val<=mid)update(ls[k],l,mid,ls[time],val); else update(rs[k],mid+1,r,rs[time],val); } int query(int k1,int k2,int l,int r,int val) { if(l==r)return l; int mid=l+r>>1; int cnt=sum[ls[k2]]-sum[ls[k1]]; if(val<=cnt)return query(ls[k1],ls[k2],l,mid,val); else return query(rs[k1],rs[k2],mid+1,r,val-cnt); } void work() { int l=read(),r=read(),val=read(); int ans=query(root[l-1],root[r],1,side,val); printf("%d\n",b[ans]); } int main() { n=read();m=read(); for(int i=1;i<=n;i++)a[i]=read(),b[i]=a[i]; sort(b+1,b+n+1); side=unique(b+1,b+n+1)-b-1; build(root[0],1,side); for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+side+1,a[i])-b; for(int i=1;i<=n;i++)update(root[i],1,side,root[i-1],a[i]); while(m--)work(); return 0; }
0/3:例题讲解
T1:kth-number(首先当然是传统例题啦)
简要题意:给出一个序列,求区间第k小的值。
简要题解:对于每一个位置维护一棵值域线段树,内容为该位置到1号位置的全部信息。
值域太大怎么办?放动态开点线段树直接无视值域。
所以我们直接上主席树即可。只不过历史版本不是时间而是位置。(这也是主席树常用的定义)
每次查询利用了前缀和思想。两个指针在两棵主席树上同步下传,查到的信息相减即为答案信息。
T2:d(某次考试题)
简要题意:给出n个矩形,可以删掉其中m个,可以任意平移,求最后重合部分最大面积。
简要题解:首先贪心显然。选择i个长最小的,m-i个宽最小的删掉一定是最优的。
所以我们按照长排序,对宽做一个裸的kth-number问题就行了。
T3:e(树上主席树还是主席树上树??)
简要题意:给出一个n个节点的树,q次询问,每次询问给出一些点,查询包含这些点的最小联通块与r最小差距值。
简要题解:首先维护一棵树上主席树,子节点建立主席树的时候继承父节点信息。
对于每次询问读入的点,可以利用倍增LCA求出他们的公共祖先。
对于每个节点到他们公共祖先的这一条链可以通过在树上主席树中的查询得到r的前驱和后继。
前驱后继查法:假如我要查询前驱。此时比较r与mid的关系。若r比mid小,前驱一定在左区间。直接向左递归查询。
若r比mid要大,此时出现一种特殊情况,即r比右区间中最小的值要小,此时需要向左区间递归查询。特判即可。
查询后继同理。