全排列问题

全排列问题

0. 参考文献

序号	文献
1	全排列算法part1
2	全排列算法part2
3	全排列算法的全面解析
4	一次搞懂全排列——LeetCode四道Permutations问题详解

在LeetCode中一共有4个和全排列相关的题目分别是：

题号	题目
31	Next Permutation
46	Permutations
47	Permutations II
60	Permutation Sequence

本文记录下在刷题过程中对于这个类题型的解法，希望对大家有所帮助。

1. 递归解法

对于全排列的求解，第一个想到的肯定是通过递归的解法。例如对于数列p(n)={1,2,3,…,n}，从中间取出一个数比如1，剩下的只需要求出p(n-1)的全排列，然后依次把1加入p(n-1)的全排列中。对于全排列也有2中方法：

1. 将取出的数(例子中是1)，依次插入到p(n-1)的全排列的不同位置上。在这里称之为插入法。
2. 首元素依次和后续的元素交换，然后求首元素之后的子序列的全排列。这里称之为首元素固定法。

相信对于2个方法的描述，大家应该还是比较模糊的。没关系后续将会详细讲解。

1.2 插入法

举个例子，比如{1, 2 , 3 }，我们知道这个序列的全排列是：

{1,2,3}
{1,3,2}
{2,1,3}
{2,3,1}
{3,1,2}
{3,2,1}

观察上面的结果，可以发现只要把1插入到{2,3}和{3,2}的各个位置，就可以获得答案。同时也可以知道{2,3}和{3,2}其实是除了1以外剩下的元素的全排列。

因此可以总结出如下的步骤：

1. 将首元素摘出来
2. 生成剩余序列的全排列
3. 将首元素插入步骤2中的序列的各个位置

实现的代码如下：

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0 : return [[]]
        ret = []
        sub_permute = self.permute(nums[1:])
        for e in sub_permute:
            
            for (index,x) in enumerate(e):
                t = list(e)
                t.insert(index,nums[0])
                ret.append(t)
                
            t = list(e)
            t.append(nums[0])
            ret.append(t)
        return ret 

1.3 首元素固定法

继续上面那个例子{1,2,3}:

{1,2,3}
{1,3,2}
{2,1,3}
{2,3,1}
{3,1,2}
{3,2,1}

是否发现生成全排列的方式也可以固定一个首元素，然后生成剩下的元素的排列，再将1和剩下的元素的排列做组合。

例如固定1 ，然后生成{2,3}的全排列是{2,3}和{3,2}。然后1和{2,3}和{3,2}组合。然后交换1和2 ，让2做首元素，在生成{1,3}的全排列{1,3}和{3,1}，在和2做组合。实现的代码如下：

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        return self.p(nums)
        
    def p(self,nums):
        
        if len(nums) == 1 :
            return [[nums[0]]]
        
        ret = []
        for i in range(len(nums)):
            nums[0],nums[i] = nums[i],nums[0]
            t = self.p(nums[1:])

            for e in t :
                t1 = list(e)
                t1.insert(0,nums[0])
                ret.append(t1)
            nums[0],nums[i] = nums[i],nums[0]
        return ret

2. 字典序法

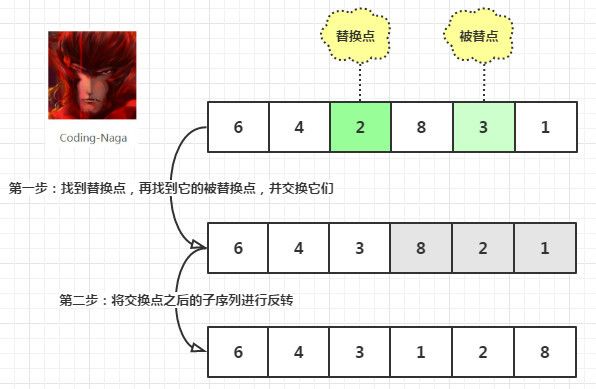
这里直接引用文献3全排列算法的全面解析中的图来说明下字典序的方法。如下图所示：

1. 然后从序列尾部开始，找到第一个开始降序的元素，称之为替换点1。例如图中是元素2
2. 再从序列尾部开始，找到第一个比替换点1大的元素，这里称之为替换点2。例如图中是元素3
3. 交换替换点1和2
4. 从替换点1下一个元素开始，到序列尾部，所有元素反正

上面的4步既是求出了当前序列的下一个比它大的序列。因此，求一个序列的全排序，可以从序列的最小排列开始，一直求到最大排列，既求得了全排列。

代码实现如下：

class Solution(object):
    def islast(self,nums):
        for i in range(0,len(nums) - 1):
            if nums[i] nums[first_index] :
                    sec_index = i
                    break
            nums[first_index],nums[sec_index] = nums[sec_index],nums[first_index]
            for i in range(first_index+1,len(nums)):
                if i<=len(nums) - 1 - (i-first_index-1):
                    nums[i],nums[ len(nums) - 1 - (i-first_index-1) ] = nums[ len(nums) - 1 - (i-first_index-1) ],nums[i]

            tmp = list(nums)
            ret.append(tmp)
            first_index = 0
            sec_index = 0
        return ret